 |
|
На підставі теореми Гауса
3.1. Неможливість стійкої рівноваги заряду в електричному полі
Нехай в вакуумі є система нерухомих точкових зарядів, які знаходяться в положенні рівноваги. Розглянемо один заряд Q, який знаходиться в замкненій поверхні S. Припустимо, що Q>0, тоді щоб рівновага була стійкою, необхідно, щоб у всіх точках S поле Е, яке утворене всіма іншими зарядами системи було направлене до Q. Лише в цьому випадку при будь-якому малому зміщенні Q з положення рівноваги на нього буде діяти повертаюча сила і положення рівноваги буде стійким. Але така конфігурація поля Е навколо Q протирічить теоремі Гауса. Потік Е крізь S буде негативним, а за теоремою Гауса він повинен дорівнювати нулю, бо цей потік створено зарядами, які розташовані зовні S. А те, що потік вектора напруженості чисельно дорівнює нулю означає, що в якихось точках поверхні S вектор Е направлений всередину, а в інших – назовні. Звідси висновок, що стійкої рівноваги заряду в будь-якому електростатичному полі не існує.
3.2. Поле рівномірно зарядженої площини
Нехай, заряд рівномірно розподілений по площині з поверхневою густиною σ. З міркувань симетрії очевидно, що вектор напруженості може бути тільки перпендикулярним до даної зарядженої площини і в симетричних відносно цієї площини точках, вектор Е однаковий за модулем і протилежний за напрямком.
Така конфігурація поля підказує, що в якості замкнутої поверхні для дослідження поля потрібно вибрати циліндр. Вважаємо, що дана поверхнева густина додатна: σ>0. Потік крізь кругову поверхню дорівнює нулю: Фб=0. Тому повний потік через всю поверхню циліндра:
Фn=2E∆S,
де ∆S – площина кожного торця циліндра.
Ззовні циліндра знаходиться певний заряд Q=σ∆S. За теоремою Гауса Фn=Q.
,
, (3.1)
Рис.3.1
En – проекція вектора Е на нормаль n до зарядженої поверхні, причому вектор нормалі направлений до даної поверхні.
Відповідно до (3.1), коли σ >0 і напруженість електричного поля Еn>0. Це означає, що вектор Е направлений від зарядженої площини.
Якщо σ<0, то Еn<0 (вектор Е направлений до зарядженої площини).
Той факт, що Е не залежить від відстані до площини означає, що відповідне електричне поле є однорідним, тобто однакове зліва і справа від даної площини.
Отриманий результат справедливий лише для нескінченної однорідної плоскої поверхні (лише в цьому випадку справедлива симетрія), але також приблизно справедливий і для прилягаючої до поверхні
частини.
Рис.3.2
3.3. Поле двох паралельних заряджених площин
Нехай кожна з площин має однакову за модулем але різну за знаком поверхневу густину заряду σ.
Поле двох заряджених площин можна знайти як суперпозицію полів, створюваних кожною площиною окремо. Між площинами напруженості полів додаються і мають однаковий напрям, тобто
. (3.2)
В даній формулі σ – модуль поверхневої густини заряду.
Рис. 3.3
Поле в даному випадку знаходиться між площинами і є однорідним в даній області. Результат справедливий і для площини кінцевих розмірів, якщо відстань між площинами набагато менша площі самих площин (плоский конденсатор).
Найбільш помітні відхилення однорідності лише поблизу пластин, але при розрахунках ними нехтують.
3.4. Поле нескінченного круглого циліндра
Нехай, поле створене нескінченною циліндричною поверхнею радіусом R і ця поверхня заряджена з постійною поверхневою густиною σ. З міркувань симетрії слідує, що напруженість поля в будь-якій точці направлена вздовж прямої, перпендикулярної осі циліндра. Величина напруженості не залежить від відстані r від осі циліндра.
Уявимо деяку коаксіальну замкнуту циліндричну поверхню радіуса r і довжини h.
Для основи циліндра En=0. Напруженість електричного поля в даному випадку перпендикулярна до поверхні циліндра.
Для бічної поверхні циліндра En=E(r).
Вважатимемо, що заряд позитивний.
З даного слідує, що потік Е через бічну поверхню чисельно дорівнює 
.
Рис.3.4
Якщо даний радіус r>R, всередину даної поверхні попаде весь заряд Q, який буде чисельно дорівнювати добутку лінійної густини даного заряду на довжину циліндра h.
Q=τh,
(τ – лінійна густина заряду).
Використаємо теорему Гауса:
;
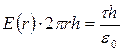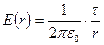. (3.3)
Формула (3.3) справедлива при r ≥R.
Якщо r<R, то замкнута поверхня не має всередині зарядів, внаслідок чого Е(r)=0.
Таким чином, всередині рівномірно зарядженої циліндричної поверхні нескінченної довжини поле відсутнє. Напруженість ззовні поверхні визначається лінійною густиною τ і відстанню r від осі циліндра.
Поле негативно зарядженого циліндра відрізняється від поля позитивно зарядженого циліндра лише напрямом вектора напруженості, але не його величиною.
З формули (3.3) слідує, що зменшуючи радіус циліндра R при незмінній лінійній густині заряду можна отримати поблизу поверхні циліндра поле з дуже великою напруженістю. Підставивши (3.3) в умову, що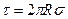 
і уявивши, що r=R, отримаємо для напруженості поля безпосередньо біля поверхні циліндра
. (3.4)
За допомогою принципу суперпозиції можна знайти поле двох коаксіальних циліндричних поверхонь з однаковою по величині але різною за знаком лінійною густиною τ. Тоді поле знаходиться між поверхнями.
Всередині меншого і ззовні більшого циліндрів поле відсутнє, а між циліндрами величина напруженості визначається за допомогою формули (3.3).
Це справедливо також для циліндричних поверхонь скінченої довжини, якщо відстань між поверхнями набагато менша їх довжини (циліндричний конденсатор). Відхилення помітні лише поблизу країв циліндра.
Рис. 3.5
3.5. Поле сферично зарядженої поверхні
Поле, створене сферичною поверхнею радіуса R, яка заряджена з поверхневою густиною σ буде центральносиметричним. Тобто напрям вектора напруженості в будь-якій точці, що проходить через центр сфери є функцією відстані R від центра сфери.
Уявимо концентричну поверхню радіуса r.
Для всіх точок цієї поверхні En=E(r).
Якщо r>R – всередину даної поверхні попаде весь заряд Q, розподілений по поверхні сфери і тому можна записати теорему Гауса:
.
З даного рівняння
, (r ≥R). (3.5)
Сферична поверхня радіуса r меншого ніж R не буде мати зарядів, внаслідок чого для випадку r<R
Еn(r)=0.
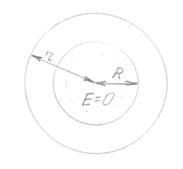Таким чином всередині сферичної поверхні з постійною поверхневою густиною поле відсутнє, ззовні даної поверхні поле тотожне з полем точкового заряду тієї ж величини, розміщеного в центрі сфери.
Використовуючи принцип накладання полів можна показати, що поле двох сферичних поверхонь, які несуть однакові заряди, але з протилежними знаками, буде знаходитись в проміжку між поверхнями, причому величина напруженості буде визначатися за формулою Е.
Рис.3.6
3.6. Поле об’ємно зарядженої кулі
Нехай куля радіусом R заряджена з постійною об’ємною густиною заряду ρ. Поле в даному випадку володіє центральною симетрією.
Для поля зовні кулі маємо той самий результат, що і для сферичної поверхні – рівняння (3.5). Але для точок всередині кулі результат інший.
Сферична поверхня (r<R) заключає в собі заряд
.
Тому теорема Гауса для такої поверхні набуде вигляду:
.
Об’ємна густина заряду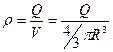 
. Підставимо це значення в попередню формулу. Тоді
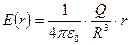, (r≤R).
Таким чином, всередині кулі напруженість зростає лінійно з відстанню r до центра, а зовні кулі – спадає із збільшенням відстані r.
Рис. 3.7
Питання для самоконтролю
1. Які бувають електричні заряди, їх властивості?
2. Що характеризує закон Кулона?
3. Які характеристики електростатичного поля ви знаєте, що вони характеризують?
4. Що собою представляють еквіпотенціальні поверхні?
5. Що називається електричним диполем?
6. Як себе поводить диполь в однорідному і неоднорідному полях?
7. Що таке потік вектора напруженості електричного поля?
8. Теореми Гауса і Остроградського-Гауса
9. Що характеризують циркуляція і ротор вектора напруженості?
10. Теорема Стокса і її використання?
11. Як розраховується поле рівномірно зарядженої площини, та двох площин?
12. Як розраховується поле зарядженої поверхні та зарядженої кулі?