 |
|
Уравнение прямой линии в пространстве
Общее уравнение плоскости
Плоскость 
в пространстве можно задать некоторой точкой 
и некоторым вектором 
, перпендикулярным плоскости. Вектор называется нормальным или направляющим вектором плоскости.
Пусть 
‑ произвольная точка плоскости . Вектор 
целиком лежит в плоскости , поэтому 
и 
‑ перпендикулярные и их скалярное произведение равно нулю:
. (1)
Уравнение (1) называется уравнением плоскости в векторном виде.
В координатной форме уравнение (1) запишется как
или
, (2)
где 
.
Уравнение (2) называется общим уравнением плоскости.
Если в уравнении (1) в качестве направляющего вектора плоскости взять единичный вектор 
, где 
, то получим нормальное уравнение плоскости:
. (3)
или в координатной форме
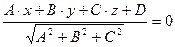. (4)
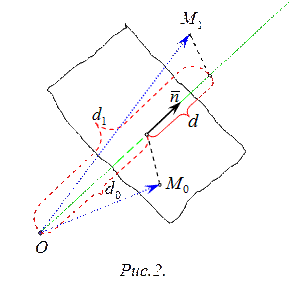
Задача. Найти расстояние 
от точки 
до плоскости , заданной уравнением (3).
Решение.
Если 
‑ начало координат и ‑ точка данной плоскости (рис.2), то 
и 
. Введем обозначения:
‑ расстояние от начала координат до плоскости, тогда справедливо равенство 
;
‑ проекция вектора 
на вектор 
, т.е.
;
‑ расстояние от точки до плоскости .
Так как 
, то имеем
.
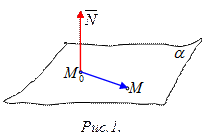
Уравнение плоскости, проходящей через три точки
Пусть , 
, 
три точки, не лежащие на одной прямой и принадлежащие плоскости (рис.1). Возьмем произвольную точку 
, тогда вектора
,
,
‑
компланарные, т.е.
(1)
Уравнение (1) – это уравнение плоскости, проходящей через три точки. Запишем это уравнение в координатной форме:
(2)
Взаимное расположение двух плоскостей.
Даны две плоскости и 
, с соответствующими направляющими векторами и 
. Если 
‑ двугранный угол между этими плоскостями, то он равен углу, образованному векторами и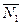 
.
Таким образом, имеем
,
где 
, 
, 
.
Отсюда получаем:
условие параллельность плоскостей
;
условие перпендикулярности плоскостей
.
Уравнение прямой линии в пространстве
Прямая 
в пространстве однозначно определяется точкой и направлением, т.е. некоторым вектором 
.
Пусть 
‑ произвольная точка прямой, тогда 
и 
коллинеарные вектора, поэтому
, 
. (1)
Уравнение (1) является векторным уравнением прямой линии в пространстве.
Запишем уравнение (1) в координатной форме. Так как и 
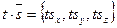, то
откуда получаем
параметрические уравнения прямой
(2)
и из равенств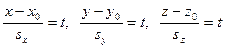 
‑
канонические уравнения прямой
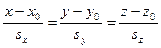. (3)
Пример 1. Написать уравнение прямой, проходящей через точку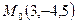 
с направляющим вектором 
.
Решение. Канонические уравнения прямой:
;
параметрические уравнения прямой:
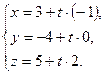
Прямую в пространстве можно задать как линию пересечения двух плоскостей:
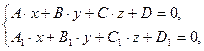(4)
с соответствующими нормалями и . В этом случае направляющий вектор 
прямой , удовлетворяет условиям 
и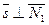 
, следовательно, можно положить 
.
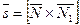Пример 2. Найти направляющий вектор прямой и его направляющие косинусы, если прямая задана как линия пересечения двух плоскостей:
Решение. 
, 
,
, 
,
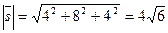