Главная | Обратная связь

Спектральный состав импульсного сигнала

 

Одной из основных теоретических задач импульсной техники является изучение методов формирования импульсов линейными и нелинейными схемами, т. е. создание импульсов необходимой формы, длительности и амплитуды.

Существуют два метода изучения работы формирующих схем — спектральный и импульсный (метод переходных характеристик). Спектральный метод, по существу, не отличается от широко распространенного метода исследования радиотехнических схем в звуковом и телевизионном вещании.

Импульсный метод исследования радиосхем, основанный на решении дифференциальных уравнений, обладает большей на­глядностью, так как он позволяет проследить за изменениями формы и других параметров импульса без промежуточного пере­хода к его «невидимым» спектральным составляющим. Однако в ряде случаев в достаточно сложных схемах решение задачи непо­средственного получения формы импульса на выходе оказывается слишком громоздким, а иногда и просто невозможным. В этих случаях предпочтительнее спектральный метод.

В каждом конкретном случае необходимо выяснить, какой из указанных методов применять рациональнее. Часто приходится использовать одновременно как спектральный, так и импульсный методы.

Любая радиосхема — усилитель, фильтр, линия задержки и т. д. — по-разному влияет на прохождение через нее сигналов низких, средних и высоких частот. Это приводит к изменению формы выходных импульсов по сравнению с входными. Чтобы пользоваться спектральным анализом работы схем в импульсном режиме, нужно иметь представление о спектре импульсного про­цесса, а также о влиянии на форму импульсов различных спект­ральных составляющих. Рассмотрим с этой целью периодическую последовательность импульсов (рисунок 4 а).

Известно, что любую периодическую функцию можно предста­вить в виде суммы гармонических составляющих (ряд Фурье):

u(t) = +

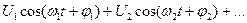
или

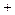
u(t) = (4)

где Uo/2 — постоянная составляющая.

Частота первой гармоники он определяется периодом Т следо­вания импульсов

(5)

все последующие гармоники кратны первой:

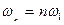
… (6)

Таким образом, периодическая последовательность импульсов имеет линейчатый спектр (рисунок 8), т. е. в нем отсутствуют составляющие с частотами, отличными от n (n — целое число), поэтому промежутки между гармониками оказываются незапол­ненными.

В общем случае каждая гармоника может иметь свою собст­венную начальную фазу . Это означает, что каждая гармоника, изображаемая в виде

 

Рисунок 8 – Спектр периоди- Рисунок 9 – Фазовые соотношения между

ческой последовательности гармоническими составляющими

импульсов

 

косинусоиды, при t=0 не выходит из начала координат (рисунок 9). Любая из составляющих ряда Фурье может быть представлена в виде суммы синусоиды и косинусоиды U_n cos (ω_nt + φ_n)=Un cos φ_n cos ω_nt —U_n sin ω_nt =

U_c cos ω_nt – U_s sin ω_nt , (7)

где U_c и U_s - амплитуды косинусоидальных и синусоидальных составляющих.

Для практических целей полезно выяснить, какая последовательность импульсов изображается только рядом синусов, а какая – только рядом косинусов и в каких случаях в состав ряда Фурье входит и то и другое. Введем понятия четной и нечетной функций. Четная функция (рисунок 10, а) характеризуется наличием симметрии относительно оси ординат О - u (симметрии первого рода). Для этой функции любая точка а имеет симметричную точку а΄ , отстоящую от оси ординат на том же расстоянии t₁ , т.е. f (+t ₁ ) = f ( - t₁ ).

 

Рисунок 10 – Параметры четных и нечетных функций: а) четная;

б) нечетная; в) функция косинуса; г) функция синуса

Если сложить рисунок 10, а по линии О - u , то левые и правые части изображенияимпульса сольются.

Нечетная функция (рисунок 10, б) также характеризуется симметрией, но относительно точки 0 - начала координат (симметрия 2-го рода). Для любой точки b найти симметричную точку b΄, если провести прямую bob΄ через начало координат.

Косинус является четной функцией, его изображение симметрично относительно оси ординат. Синус – нечетная функция, его изображение симметрично относительно «начала координат (рисунок 10,в,г).

Четная функция определяется условием

u(t)= + u(- t), (8)

нечетная – условием

u(t)= - u(- t). (9)

Например, .

Любая периодическая четная функция представляется рядом косинусоидальных гармонических составляющих. В свою очередь, нечетная функция представляется только рядом синусоид. При отсутствии в импульсах симметрии 1 и 2 рода соответствующий ряд Фурье будет содержать как синусоидальные, так и косинусоидальные составляющие.

Амплитуды гармоник спектральных составляющих определяются следующими формулами:

U_cn = 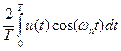, (10)

 

U_sn = , (11)

где U_cn , U_sn – амплитуды n-й косинусоидальной и синусоидальной гармоник соответственно.

В качестве примеров, иллюстрирующих применение ряда Фурье, рассмотрим спектральный состав последовательности двух видов импульсов: симметричных прямоугольных и экспоненциальных.

Так как рисунок 11, а представляет собой график четной функции (синусоидальные составляющие отсутствуют), для нахождения распределения амплитуд гармоник по частотам можно воспользоваться только формулой (10). Учитывая, что на участке 0 -T при 0< t < u(t)=U=const, а при

< t < T u (t)=0 , можно ввести следующие пределы интегрирования:

U_cn = ‌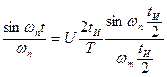 . (12)

Введем в формулу (12) обозначения: .

U_cn = . (13)

На рисунке 11,а представлен график U_cn= f (n) (для примера взято U/Q=1,

n=0,1,2, … - номер гармоники, причем n=0 означает постоянную составляющую). Как следует из графика, амплитуды спектральных составляющих убывают с ростом частоты и достигают нуля только при бесконечно высокой частоте.

 

 

Рисунок 11 – Форма и спектральный состав импульсов: а) прямоугольных; б) экспоненциальных

 

Пример 2.

Экспоненциальные импульсы (рисунок 11, б). От момента t = 0 (начало координат) и далее форма импульса определяется экспонентой

u=Ue^-t/τ , (14)

где τ – постоянная времени.

Так как данные импульсы не являются четными или нечетными функциями времени, в их спектре содержатся как косинусоидальные, так и синусоидальные составляющие. Амплитуды этих составляющих определяются по формулам (10) и (11). Косинусоидальные составляющие

 

U_cn = _.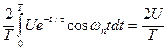

После подстановки пределов и простых преобразований получаем

U_cn= 2U 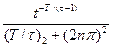. (15)

Синусоидальные составляющие

U_sn = .

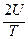
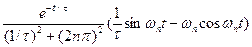После подстановки пределов и простых преобразований имеем

U_sn = 4 . (16)

 

Полная амплитуда n-й гармоники спектра определяется как корень квад­ратный из суммы квадратов косинусоидальной и синусоидальной составляющих:

U_n = 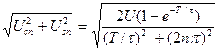. (17)

 

На рисунке 11,б представлен также график зависимости U_n=f(n), соответст­вующий формуле (17).