ПРЯМІ ЛІНІЇ ТА ПЛОЩИНИ.

Побудова лінії в полярній системі координат.

А) Короткі теоретичні відомості

У ряді випадків побудування ліній за рівнянням виду F(x;y)=0 у прямокутній декартовій системі координат досить проблематично, в той же час, побудова цієї лінії в полярній системі координат за даним рівнянням r=f(j) значно полегшує задачу.

Для переходу від декартових координат до полярних використовується формула: y= rsіn(j) , x=rcos(j) (1) , де 0£r<2p. При цьому декартова і полярна координат система розміщені так, що полярна ось співпадає з додатною частиною осі ОХ.

б) Порядок роботи:

1) Підставити значення х та у з формул (1) в дане рівняння лінії та знайти її рівняння у полярних координатах у виді r=f(j).

2) Придаючи значення через проміжок, який дорівнює 15^о(p/12 радіан) та обчислюючи відповідні значення r (за допомогою спеціальної таблиці або калькулятора), скласти таблицю відповідних значень r та j. (При необхідності можна взяти інші значення j через проміжки менш 15^о

Обов’язково включити в таблицю ті значення j, яким відповідає найменше значення r.

Підрахунки необхідно округляти з точністю до 0,01, кінцеві приблизні значення округлити з точністю до 0,1.

За даними отриманої таблиці побудувати в полярній системі координат (залишаючи і декартову систему на малюнку) відповідні точки. З’єднуючи ці точки плавною кривою, побудувати лінію.

В) Умови для задач № 1-30

За допомогою переходу від декартових координат до полярних побудувати лінію, задану рівнянням:

№1

№2

№3

№4

№5

№6

№7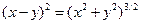

№8

№9

№10

№11

№12

№13

№14

№15

№16

№17

№18

№19

№20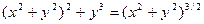

№21

№22

№23

№24

№25

№26

№27

№28

№29

№30

Границі. Неперервність

Обчислити границі заданих функцій.

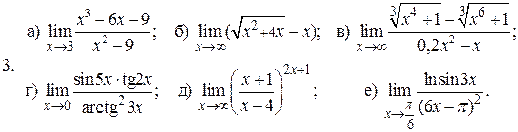
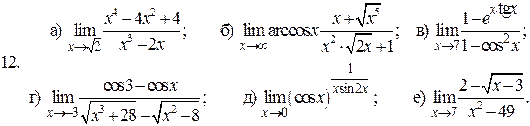
Диференціальне числення функцій однієї змінної.

Задача 1.

Продиференціювати задані функції.

У пунктах а), б), в), г), д) знайти похідні ; у пункті е) знайти ; у пункті є) знайти

Варіанти завдань

Задача 2.

Знайти границі, використовуючи правило Лопіталя.

Варіанти завдань

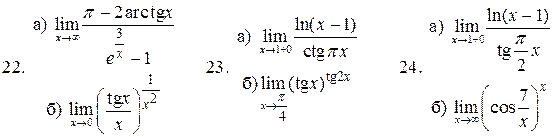
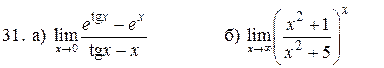
ПРЯМІ ЛІНІЇ ТА ПЛОЩИНИ.

1. Пряма на площині.

Наведемо основні види рівнянь прямої на площині:

1) А(х-х₀)+В(y-y₀)=0 — рівняння прямої, що проходить через точку М₀(x₀,y₀) перпендикулярно до нормального вектора ;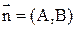

2) Ах+Ву+С=0 — загальне рівняння прямої, де вектор 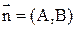— нормальний вектор прямої;

3) y=kx+b — рівняння прямої з кутовим коефіцієнтом; k — кутовий коефіцієнт прямої: —кут між прямою і додатним напрямом осі О_х, b — ордината точки перетину прямої з віссю О_у;

4) у-у₀=k(х-х₀) — рівняння прямої, що проходить через задану точку М₀(x₀,y₀) у заданому напрямі, який задається кутовим коефіцієнтом k;

5) — рівняння прямої, що проходить через точку М₀(x₀,y₀) паралельно напрямному вектору (канонічне рівняння);

6) — параметричні рівняння прямої, де — параметр. Ці рівняння у векторній формі мають вигляд:

де — радіус-вектор точки М₀(x₀,y₀), що належить прямій, — напрямний вектор прямої;

7) — рівняння прямої у відрізках, де а і b — величини напрямлених відрізків, що відтинаються прямою на координатних осях;

8) — рівняння прямої, що проходить через дві задані точки М₁(х₁,у₁) і М₂(х₂,у₂);

9) — нормальне рівняння прямої, де — напрямні косинуси нормального вектора — відстань від початку координат до прямої.

Загальне рівняння прямої Ах+Ву+С=0 приводиться до

нормального вигляду множенням на нормувальний множник

де знак перед коренем вибирається протилежним знаку вільного

члена С.

Якщо — нормальні вектори прямих відповідно, то кут між ними визначається за формулою:

Якщо k1, k2 — кутові коефіцієнти двох прямих, то кут φ між ними визначається за формулою:

Умова паралельності та перпендикулярності прямих :

або

Якщо задане рівняння прямої : Ах+Ву+С=0 і точка М₀(x₀,y₀), то відстань від цієї точки до даної прямої обчислюється за формулою:

2. Площина та прямі у просторі.

1) А(x-х₀)+В(у-y₀)+С(z-z₀)=0 — рівняння площини, що проходить через задану точку М₀(x₀,y₀,z₀) перпендикулярно до нормального вектора ;

2) Aх+Bу+Cz+D=0 — загальне рівняння площини, де вектор — нормальний вектор площини;

3) — рівняння площини у відрізках, де a, b, c — довжини напрямлених відрізків, що відтинаються площиною на координатних осях;

4) 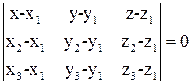— рівняння площини, що проходить через три задані точки M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃);

5) — нормальне рівняння площини, де — напрямні косинуси нормального вектора — відстань від початку координат до площини.

Загальне рівняння площини Aх+Bу+Cz+D=0 приводиться до нормального вигляду множенням на нормувальний множник

де знак перед коренем вибирається протилежним знаку вільного

члена D.

Кут між двома заданими площинами визначається за формулою

Умови паралельності та перпендикулярності двох площин

мають вигляд:

Відстань ρ(M₀,Q) від точки M₀(x₀,y₀,z₀) до площини Q: Aх+Bу+Cz+D=0:

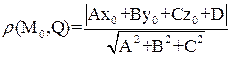3. Пряма у просторі.

Основні види рівнянь прямої у просторі:

1) — загальні рівняння прямої, що визначена перетином двох непаралельних площин;

2) — параметричне рівняння прямої в просторі, де

— параметр.

Ці рівняння у векторній формі мають вигляд:

— радіус-вектор точки М₀(x₀,y₀,z₀),

що належить прямій, — напрямний вектор прямої;

3) — канонічні рівняння прямої, де А₀(x₀,y₀,z₀) — задана точка прямої, а вектор — напрямний вектор прямої;

4) — рівняння прямої , що проходить через дві задані точки М₁(x₁,y₁,z₁) і M₂(x₂,y₂,z₂).

Кут між прямими

обчислюється за формулою:

Умови паралельності та перпендикулярності прямих L₁ та L₂:

Відстань ρ(М₀,L) від точки М₀ до прямої L, де

L: , точка А(x₁,y₁,z₁) L, , визначається за формулою

Щоб знайти точку перетину прямої і площини Aх+Bу+Cz+D=0, слід розв’язати спільно ці рівняння.

Кут між прямою L: і площиною Q: Aх+Bу+Cz+D=0 визначається за формулою:

Умови паралельності та перпендикулярності прямої L та Q:

Умова належності двох прямих

одній площині така:

Прямі L₁ та L₂ мимобіжні, якщо

Відстань між двома мимобіжними прямими L₁ та L₂ визначається за формулою:

1. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон x+y-1=0 и y+1=0, если известно, что диагонали параллелограмма пересекаются в точке P(-1, 0).

2. На прямой 2x+y+11=0 найти точку, равноудаленную от двух данных точек А(1,1) и В(3,0).

3. Найти координаты точки, симметричной точке А(2,-4) относительно прямой 4x+3y+1=0.

4. Вычислить координаты центра окружности, описанной около треугольника с вершинами А(-1,1), В(2,-1), С(4,0).

5. Составить уравнение прямой, проходящей через точку А(2,6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв. ед.

6. Составить уравнение прямой, проходящей через точку А(-1,2) так, середина ее отрезка, заключенного между параллельными прямыми x+2y+1=0 и x+2y-3=0, лежит на прямой x-y-6=0.

7. Даны уравнения двух сторон треугольника 4x-5y+9=0 и x+4y-3=0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке Р(3,1).

8. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2x-y+4=0 и 2x-y+10=0 и уравнение одной из его диагоналей x+y+2=0.

9. Составить уравнение сторон треугольника, если А(-5,5) и В(3,1) – две его вершины, а D(2,5) – точка пересечения его высот.

10. Дано уравнение одной из сторон квадрата x+3y-7=0 и точка пересечения его диагоналей Р(0,-1). Найти уравнения трех остальных сторон этого квадрата.

11. Уравнение одной из сторон квадрата x+3y-5=0. Составить уравнения трех остальных сторон квадрата, если Р(-1,0) – точка пересечения его диагоналей. Сделать чертеж.

12. Даны уравнения одной из сторон ромбаx-3y+10=0 и одной из его диагоналей x+4y-4=0; диагонали ромба пересекаются в точке Р(0,1). Найти уравнения остальных сторон ромба. Сделать чертеж.

13. Уравнения двух сторон параллелограмма x+2y+2=0 и x+y-4=0, а уравнение одной из его диагоналей x-2=0. Найти координаты вершин параллелограмма. Сделать чертеж.

14. Даны вершины А(-3,-2), В(4,-1), С(1,3) трапеции ABCD (AD║BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.

15. Даны уравнения двух сторон треугольника 5x-4y+15=0 и 4x+y-9=0. Его медианы пересекаются в точке Р(0,2). Составить уравнение третьей стороны треугольника. Сделать чертеж.

16. Даны две вершины А(2,-2) и В(3,-1) и точка Р(1,0)пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.

17. Даны уравнения двух высот треугольника x+y=4 и y=2x и одна из его вершин А(0,2). Составить уравнения сторон треугольника. Сделать чертеж.

18. Даны уравнения двух медиан треугольника x-2y+1=0 и y-1=0 и одна из его вершин А(1,3). Составить уравнения его сторон. Сделать чертеж.

19. Две стороны треугольника заданы уравнениями 5x-2y-8=0 и 3x-2y-8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертеж.

20. Составить уравнение и построить линию, расстояние каждой точки которой от начала координат и от точки А(5,0) относятся как 2:1.

21. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(-1,0) вдвое меньше расстояния ее от прямой x=-4.

22. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(2,0) и от прямой 5x+8=0 относятся, как 5:4.

23. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4,0), чем от точки В(1,0).

24. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2,0) и от прямой 2x+5=0 относятся, как 4:5.

25. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(3,0)вдвое меньше расстояния от точки В(26,0).

26. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0,2) и от прямой y-4=0.

27. Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности .

Замечание. Напомним, что за расстояние от точки А до фигуры Ф принимается наименьшее из расстояний между точкой А и точками фигуры Ф.

28. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2,6) и от прямой y+2=0.

29. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(-4,0) втрое дальше, чем от начала координат.