 |
|
II. Физические основы механики. Модуль №2
Сборник тестовых контрольных заданий (модулей)
По физике 1-го уровня сложности
Утверждено Редакционно – издательским советом
университета в качестве практического пособия
Курск 2007
УДК 531/534
ББК В21
К265
Рецензенты:
Доктор физико-математических наук,
зав. кафедрой «Теоретическая и экспериментальная физика» Курского государственного технического университета, профессор А.А. Родионов
Доктор физико-математических наук,
зав. кафедрой «Общая физика» Курского государственного
университета, профессор Ю.А. Неручев
Кандидат технических наук, зав. кафедрой «Физика» Курской сельскохозяйственной академии им. профессора И.И. Иванова
Д.И. Якиревич
Карпова, Г.В. Сборник тестовых контрольных заданий (модулей) по физике 1-го уровня сложности:практическое пособие. [Текст]: /Г.В. Карпова, В.М. Полунин, Г.Т. Сычев; Курск. гос. техн. ун-т. Курск, 2007. 119 с.: Ил. 101. Библиограф.: 109 с.
Практическое пособие составлено в соответствии с требованиями Государственного образовательного стандарта, Примерной программы дисциплины «Физика» и рабочей программы по физике для студентов инженерно-технических специальностей КурскГТУ.
Излагаются тестовые контрольные задания (модули) по механике и молекулярной физике для выполнения индивидуальных заданий. Содержит варианты заданий, основные формулы, необходимые приложения и таблицы. Предназначено для индивидуальной самостоятельной работы по физике студентов инженерно-технических специальностей всех формы обучения.
УДК 531/534
ББК В21
К265
Ó Курский государственный технический университет, 2007
Ó Карпова Г.В., Полунин В.М., Сычев Г.Т., 2007
Оглавление
Предисловие………………………………………………………..4
Общие методические указания к решению задач
и выполнению контрольных заданий (модулей).………………..6
I. Физические основы механики. Модуль №1.
(Кинематика и динамика. Колебания и волновые
процессы).………..............................................................................7
II. Физические основы механики. Модуль №2
(Энергия, работа, мощность. Законы сохранения в
механике. Поле тяготения. Движение в поле центральных
сил. Элементы специальной теории относительности).……..38
III. Основы молекулярной физики и термодинамики.
Модуль №3 (Конденсированное состояние. Кинематика
и динамика жидкостей. Основные понятия, определения
и законы молекулярной физики и термодинамики.
Статистический метод исследования. Основы
термодинамики. Реальные газы. Фазовые равновесия
и превращения. Кинетические явления).………………………...68
Заключение………………………………………………………108
Библиографический список…………………………………….109
Приложение 1. …………………………………………………..110
Приложение 2. …………………………………………………..114
Приложение 3. ………………………………………………......115
Предисловие
Данное практическое пособие (практикум) предназначено для улучшения организации индивидуальной самостоятельной работы студентов технических специальностей при изучении физики. Основной целью данного пособия является выяснение знаний студентов основных понятий, законов и формул, выявление индивидуального умения каждого студента применять полученные теоретические знания к решению практических задач, уровень и качество их физической подготовки, глубину и прочность навыков, необходимых студентам в процессе их дальнейшей деятельности.
Практикум составлен в соответствии с требованиями ГОСов, рабочей программы и рабочих учебных планов технических специальностей и соответствует основным задачам освоения курса физики.
Практическое пособие предназначено для студентов дневной и заочной форм обучения.
В практикуме пособии в определенной последовательности даны варианты контрольных заданий (модулей), состоящие из тестовых задач для самостоятельного решении по таким разделам курса общей физики как «Физические основы механики», «Основы молекулярной физики и термодинамики». Всего каждое тестовое задание содержит 25 вариантов. Даны общие методические указания к выполнению тестовых контрольных заданий (модулей), основные формулы курса общей физики.
Представлены необходимые при решении задач правила приближенных вычислений и таблицы.
Особо необходимо отметить наличие в пособии рисунков, поясняющих условия задач для самостоятельного решения.
Основным отличием данного практического пособия является то, что он является сборником тестовых контрольных заданий (модулей) по физике 1-го уровня сложности, что отсутствует в ранее изданной литературе по физике. Оно охватывает все разделы физики, изучаемые студентами 1 курса.
В нем каждому студенту предлагается выполнить письменное задание (модуль), состоящей из определенного количества тестовых задач.
Задача считается решенной правильно, если полученный студентом, в ходе ее решения, ответ полностью соответствует одному из приведенных в задаче.
За каждую правильно решенную задачу студент получает определенное число баллов, которое определяется рейтинговой накопительной системой.
Тестовое задание (модуль) выполняется студентами в процессе самостоятельной работы в семестре. Использование справочной литературы допускается.
Выполненный и зачтенный модуль является промежуточной аттестацией индивидуальной самостоятельной работы студента в семестре.
Предполагается, что, работая с данным практикумом, студенты будут пользоваться не только им, но и задачниками (другими пособиями, справочниками по физике), в которых они найдут необходимый теоретический и справочный материалы.
Авторы, при подборе задач, руководствовались следующим принципом: «Задачи должны быть такими, чтобы при их решении основное внимание уделялось физической стороне вопроса».
Большинство задач для самостоятельного решения, приведенных в данной работе, взято из задачников. Многие задачи переработаны. Часть задач составлена авторами практического пособия.
В приложении приведены основные формулы и законы, некоторые правила приближенных вычислений и справочные таблицы. В конце практикума приведен библиографический.
Изложение материала в данной работе предусматривает знание студентами математики в объеме школьной программы. Кроме того, предполагается, что студенты уже изучили или изучают параллельно читаемому курсу соответствующий «вузовский» материал (дифференциальное и интегральное исчисление, анализ функций, дифференциальные уравнения, векторную алгебру, ряды).
Обозначения единиц измерения физических величин даны через основные и производные единицы системы СИ.
Авторы будут благодарны всем, кто внимательно просмотрит данное практическое пособие и выскажет определенные замечания по существу. Кроме того, они постараются учесть все рациональные замечания со стороны коллег – физиков, студентов и внести соответствующие исправления и дополнения.
ОБЩИЕ методические УКАЗАНИЯ К ВЫПОЛНЕНИЮ тестовых контрольных заданий (мОДУЛЕЙ)
Контрольное задание (модуль) или контрольную работу нужно выполнять в тетради, оформленной по соответствующей форме. Условия задач необходимо переписать полностью без сокращений. Для замечаний преподавателя на странице тетради нужно оставлять поля.
В конце контрольного задания (модуля) или контрольной работы необходимо указать, каким учебником или учебным пособием студент пользовался при изучении данного раздела физики (название учебника, автор, год издания). Это необходимо для того, чтобы преподаватель, проверяющий модуль (контрольную работу), в случае необходимости смог указать, что следует студенту изучить для завершения работы.
Студенты безотрывных форм обучения зачтенную контрольную работу предъявляют экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач.
Решение задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда это необходимо, дать чертеж, выполненный с помощью чертежных принадлежностей. Решить задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин. После получения расчетной формулы, для проверки правильности полученного результата, следует применить правило размерности. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах системы СИ. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение соответствующего числа на соответствующую степень десяти. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Это относится и к случаю, когда результат получен с применением калькулятора или ЭВМ.
I. Физические основы механики. Модуль №1
(Кинематика и динамика. Колебания и волновые процессы)
Вариант № 1
1. Первую половину времени своего движения автомобиль двигался со скоростью v1=80 км/ч, а вторую половину времени – со скоростью v2=40 км/ч. Какова средняя скорость движения <v> движения автомобиля?
Ответ: а) <v>=50 км/ч; б) <v>=70 км/ч; в) <v>=6 км/ч;
г) <v>=80 км/ч; д) <v>=60 км/ч.
2. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям x=3cos[2p(t+0,5)]; y=4cos(2pt). Найти уравнение траектории движения точки.
Ответ: а)  ; б)
; б) 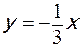 ; в)
; в) 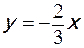 ; г)
; г)  ;
;
д)  .
.
3. Тело массой m=0,5 кг движется прямолинейно, причем зависимость пройденного телом пути S от времени t дается уравнением S=A-Bt+5t2-t3. Найти силу F, действующую на тело в конце первой секунды движения.
Ответ: а) F=0,2 Н; б) F=2 Н; в) F=3,5 Н; г) F=0,35 Н;
д) F=0,25 Н.
 4. На гладком столе лежит брусок массой m=4 кг (рис. 1). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти силу натяжения, действующую на первую гирю. Массой блоков и трением пренебречь.
4. На гладком столе лежит брусок массой m=4 кг (рис. 1). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти силу натяжения, действующую на первую гирю. Массой блоков и трением пренебречь.
Ответ: а) Т1=31,2 Н; б) Т1=21,2 Н; в) Т1=11,2 Н; г) Т1=1,12 Н;
д) Т1=0,112 Н.
5. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через центр масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
 Ответ: а) M=3,25 Н×м; б) M=2,25 Н×м;
Ответ: а) M=3,25 Н×м; б) M=2,25 Н×м;
в) M=1,25 Н×м; г) M=0,25 Н×м; д) M=0,125 Н×м.
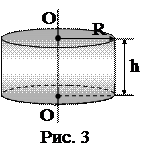
 6. На барабан радиусом R=0,5 м намотан шнур, к концу которого привязан груз массой 10 кг (рис. 3). Найти момент инерции барабана, если известно, что груз опускается с ускорением a=2,04 м/с2.
6. На барабан радиусом R=0,5 м намотан шнур, к концу которого привязан груз массой 10 кг (рис. 3). Найти момент инерции барабана, если известно, что груз опускается с ускорением a=2,04 м/с2.
Ответ: а) I=9,6 кг×м2; б) I=19,6 кг×м2; в) I=29,6 кг×м2; г) I=39,6 кг×м2; д) I=49,6 кг×м2.
7. Материальная точка массой 0,05 кг совершает гармонические колебания, уравнение которых имеет вид x=0,1sin5pt. Найти силу, действующую на точку в момент, когда фаза колебаний равна 30о.
Ответ: а) F=-0,92 Н; б) F=-0,82 Н; в) F=-0,72 Н; г) F=-0,62 Н;
д) F=-0,52 Н.
Вариант № 2
1. Первую половину своего пути автомобиль двигался со скоростью v1=80 км/ч, а вторую половину пути – со скоростью v2=40 км/ч. Какова средняя скорость движения <v> движения автомобиля?
Ответ: а) <v>=53,3 км/ч; б) <v>=63,3 км/ч; в) <v>=73,3 км/ч;
г) <v>=43,3 км/ч; д) <v>=33,3 км/ч.
2. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям: x=3coswt и y=2sinwt. Найти уравнение траектории точки.
Ответ: а)  ; б)
; б)  ; в)
; в) 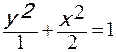 ;
;
г)  ; д)
; д)  .
.
3. Материальная точка массой 2 кг движется под действием некоторой силы согласно уравнению x=2+5t+t2-0,2t3. Найти значение этой силы в момент времени t=2 с.
Ответ: а) Т=0,8 Н; б) Т=1,8 Н; в) Т=-0,8 Н; г) Т=-1,8 Н; д) Т=2,8 Н.
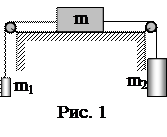 4. На гладком столе лежит брусок массой m=4 кг (рис. 1). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2кг. Найти силу натяжения, действующую на вторую гирю. Массой блоков и трением пренебречь.
4. На гладком столе лежит брусок массой m=4 кг (рис. 1). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2кг. Найти силу натяжения, действующую на вторую гирю. Массой блоков и трением пренебречь.
Ответ: а) Т=46,8 Н; б) Т=36,8 Н; в) Т=26,8 Н; г) Т=16,8 Н;
д) Т=6,8 Н.
 5. Диск радиусом R=0,5 м и массой m=2 кг (рис. 2) вращается с угловым ускорением 5 с–2 вокруг оси, проходящей через точку расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости. Определить величину вращающего момента.
5. Диск радиусом R=0,5 м и массой m=2 кг (рис. 2) вращается с угловым ускорением 5 с–2 вокруг оси, проходящей через точку расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости. Определить величину вращающего момента.
Ответ: а) M=4,88 Н×м; б) M=3,88 Н×м; в) M=2,88 Н×м;
г) M=1,88 Н×м; д) M=0,88 Н×м.
 6. На барабан массой M=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение груза. Барабан считать однородным цилиндром (рис. 3). Трением пренебречь.
6. На барабан массой M=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение груза. Барабан считать однородным цилиндром (рис. 3). Трением пренебречь.
Ответ: а) a=5 м/с2; б) a=3 м/с2; в) a=1 м/с2;
г) a=7 м/с2; д) a=4 м/с2.
7. Материальная точка массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид x=0,2sin8pt. Найти численное значение возвращающей силы в момент времени t=0,1с.
Ответ: а) F=0,54 Н; б) F=0,74 Н; в) F=1,4 Н; г) F=0,94 Н;
д) F=0,84 Н.
Вариант № 3
1. Уравнение движения материальной точки имеет вид x=2+t–0,5t2. Найти скорость v точки в момент времени t=2 с.
Ответ: а) v=-2 м/с; б) v=1 м/c; в) v=-1 м/с; г) v=2 м/с; д) v=-2,5 м/с.
2. Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 0,05 м, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение равно 0,025 м.
Ответ: а) v=140 м/с; б) v=14 м/с; в) v=1,4 м/с; г) v=0,14 м/с;
д) v=0,014 м/с.
3. Материальная точка движется под действием некоторой силы согласно уравнению Х=2+5t+t2-0,2t3. В какой момент времени значение этой силы равно нулю?
Ответ: а) t=5,67 с; б) t=1,67 с; в) t=2,67 с; г) t=4,67 с; д) t=3,67 с.
4. К потолку трамвайного вагона подвешен на нити шар. Вагон тормозит, и его скорость изменяется за время 3 с от 18 км/ч до 6 км/ч. На какой угол отклонится при этом нить с шаром?
Ответ: а) a=36,5о; б) a=26,5о; в) a=16,5о; г) Т=16,8 Н; д) a=6,5о.
 5. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку, расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 1). Определить величину вращающего момента.
5. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку, расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 1). Определить величину вращающего момента.
Ответ: а) M=0,075 Н×м; б) M=0,75 Н×м;
в) M=1,75 Н×м; г) M=2,75 Н×м; д) M=3,75 Н×м.
6. Момент силы, действующий на тело, равен 9,8 Н×м. Через 10с после начала вращения тело достигло угловой скорости 4 с-1. Найти момент инерции тела.
Ответ: а) I=4,5 кг×м2; б) I=14,5 кг×м2; в) I=24,5 кг×м2;
г) I=34,5 кг×м2; д) I=44,5 кг×м2.
7. Точка совершает гармонические колебания, уравнение которых имеет вид x=5sin(3/2)pt. Найти момент времени, когда точка имеет фазу колебаний 0,927 рад.
Ответ: а) t=0,2 с; б) t=0,3 с; в) t=0,4 с; г) t=0,5 с; д) t=0,6 с.
Вариант № 4
1. Уравнение движения материальной точки вдоль оси X имеет вид x=2+t-0,5t2. Найти ускорение a точки.
Ответ: а) a=2 м/с2; б) a=-2 м/с2; в) a=-1 м/с2; г) a=1 м/с2;
д) a=1,2 м/с2.
2. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний T=24с, начальная фаза j0=0.
Ответ: а) t=1 с; б) t=1,5 с; в) t=2 с; г) t=2,5 с; д) t=3 с.
3. Под действием постоянной силы 10 Н тело движется прямолинейно так, что зависимость пройденного телом расстояния от времени задается уравнением S=5-2t+t2. Найти массу тела.
Ответ: а) m=5 кг; б) m=7 кг; в) m=9 кг; г) m=11 кг; д) m=15 кг.
4. Найти силу тяги, развиваемую двигателем автомобиля, движущегося в гору с ускорением 1 м/с2. Уклон горы равен 1 м на каждые 25 м пути. Масса автомобиля 1 т. Коэффициент трения равен 0,1.
Ответ: а) Fт=2,37×103 Н; б) Fт=5,37×103 Н; в) Fт=7,37×103 Н;
г) Fт=9,37×103 Н; д) Fт=11,37×103 Н.

5. Тонкий стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением e=3 рад/c2 около оси, проходящей через середину стержня перпендикулярно к его длине (рис. 1). Определить величину вращающего момента M.
Ответ: а) М=0,025 Н×м; б) М=0,035 Н×м;
в) М=0,045 кг×м2/c2; г) М=0,055 Н×м; д) М=0,065 кг×м2/c2.
6. Сплошной шар массой m=1 кг и радиусом R=5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением j=4+2t+t2. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу.
Ответ: а) F=0,44 Н; б) F=0,34 Н; в) F=0,24 Н; г) F=0,14 Н;
д) F=0,04 Н.
7. Чему равен период колебаний математического маятника длиной l=1 м, находящегося в трамвайном вагоне, движущемся горизонтально с ускорением a=7 м/с2?
Ответ: а) T=0,8 с; б) T=1,8 с; в) T=2,8 с; г) T=3,8 с; д) T=4,8 с.
Вариант № 5
1. Две материальные точки движутся согласно уравнениям x1=10+t+2t2 и x2=3+2t+0,2t2. В какой момент времени скорости этих точек одинаковы?
Ответ: а) t=2 с; б) t=3 с; в) t=0,28 с; г) t= -2,8 с; д) t=2,8 с.
2. Начальная фаза гармонического колебания j0=0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
Ответ: а) t=T/4; б) t=T/5; в) t=T/3; г) t=T/2; д) t=T/6.
3. Сила F сообщает телу массой m1=2 кг ускорение a1=1 м/с2. Телу какой массы эта сила сможет сообщить ускорение 2 м/с2?
Ответ: а) m=3 кг; б) m=5 кг; в) m=1,5 кг; г) m=2,5 кг; д) m=1 кг.
 4. Тело массой 5 кг брошено под углом 30о к горизонту с начальной скоростью 20 м/с (рис. 1). Пренебрегая сопротивлением воздуха, найти изменение импульса тела за время полета.
4. Тело массой 5 кг брошено под углом 30о к горизонту с начальной скоростью 20 м/с (рис. 1). Пренебрегая сопротивлением воздуха, найти изменение импульса тела за время полета.
Ответ: а) Dp=200 (кг×м)/с; б) Dp=100 (кг×м)/с; в) Dp=50 (кг×м)/с; г) Dp=10 (кг×м)/с; д) Dp=5 (кг×м)/с.
 5. Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии l=0,25 м от середины стержня перпендикулярно к его длине (рис. 2). Определить угловое ускорение стержня.
5. Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии l=0,25 м от середины стержня перпендикулярно к его длине (рис. 2). Определить угловое ускорение стержня.
Ответ: а) e=7 с-2; б) e=6 с-2; в) e=5 с-2; г) e=4 с-2; д) e=3 с-2.
6. Сплошной шар массой m=1 кг и радиусом R=5 см вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. После прекращения действия силы шар останавливается. Закон вращения шара выражается уравнением j=1+4t-5t2. Определить тормозящий момент.
Ответ: а) М=5 Н×м; б) М=37 Н×м; в) М=55 Н×м; г) М=75 Н×м;
д) М=100 Н×м.
7. Определить период колебаний математического маятника длиной l=1 м в лифте, движущемся вертикально с ускорением a=2м/с, направленным вверх.
Ответ: а) T=3,83 с; б) T=2,83 с; в) T=1,83 с; г) T=0,83 с;
д) T=0,083 с.
Вариант № 6
1. Первую половину времени своего движения автомобиль двигался со скоростью v1=80 км/ч, а вторую половину времени – со скоростью v2=40 км/ч. Какова средняя скорость <v> движения автомобиля?
Ответ: а) <v>=50 км/ч; б) <v>=70 км/ч; в) <v>=6 км/ч;
г) <v>=80 км/ч; д) <v>=60 км/ч.
2. Две материальные точки движутся согласно уравнениям x1=4t+8t2-16t3 и x2=2t-4t2+t3. В какой момент времени ускорения этих точек будут одинаковы?
Ответ: а) t=0,54 с; б) t=0,44 с; в) t=0,34 с; г) t=0,24 с; д) t=0,14 с.
 3. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. С каким ускорением будут двигаться бруски, если к одному из них приложить силу в F=10 Н, направленную горизонтально (рис. 1)? Трением пренебречь.
3. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. С каким ускорением будут двигаться бруски, если к одному из них приложить силу в F=10 Н, направленную горизонтально (рис. 1)? Трением пренебречь.
Ответ: а) а=2 м/с2; б) а=0,2 м/с2; в) а=0,02 м/с2; г) а=1,2 м/с2;
д) а=3,2 м/с2.
 4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через центр масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через центр масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
Ответ: а) M=3,25 Н×м; б) M=2,25 Н×м;
в) M=1,25 Н×м; г) M=0,25 Н×м; д) M=0,125 Н×м.
 5. Тонкий стержень массой 300 г вращается с угловым ускорением e=4 рад/c2 под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии d=0,25 м от середины стержня перпендикулярно к его длине. Определить длину стержня (рис. 3).
5. Тонкий стержень массой 300 г вращается с угловым ускорением e=4 рад/c2 под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии d=0,25 м от середины стержня перпендикулярно к его длине. Определить длину стержня (рис. 3).
Ответ: а) l=0,4 м; б) l=0,5 м; в) l=0,6 м;
г) l=0,7 м; д) l=0,8 м.
6. Определить период колебаний математического маятника длиной l=1 м в лифте, движущемся вертикально с ускорением a=1,8м/с2, направленным вниз.
Ответ: а) T=5,2 с; б) T=4,2 с; в) T=3,2 с; г) T=2,2 с; д) T=1,2 с.
7. Определить собственную частоту колебаний моста, по которому запрещается движение взводу солдат, идущих строевым шагом. Длина шага равна 0,8 м. Длина моста 96 м. Предполагаемое время движения солдат по мосту 1 мин.
Ответ: а) n=2 Гц; б) n=1 Гц; в) n=0,5 Гц; г) n=3 Гц; д) n=4 Гц.
Вариант № 7
1. Первую половину своего пути автомобиль двигался со скоростью v1=80 км/ч, а вторую половину пути – со скоростью v2=40 км/ч. Какова средняя скорость движения <v> движения автомобиля?
Ответ: а) <v>=53,3 км/ч; б) <v>=63,3 км/ч; в) <v>=73,3 км/ч; г) <v>=43,3 км/ч; д) <v>=33,3 км/ч.
2. Две материальные точки движутся согласно уравнениям x1=4t+8t2-16t3 и x2=2t-4t2+t3. Найти скорости этих точек в момент времени, когда их ускорения одинаковы.
Ответ: а) v1=36 м/с; v2=17 м/с; б) v1=3,6 м/с; v2=17 м/с;
в) v1=5,6м/с; v2=-17 м/с; г) v1=17 м/с; v2=-39,6 м/с; д) v1=39,6 м/с;
v2=-17 м/с.
 3. Два бруска массами m1=1 кг и m2=4 кг (рис. 1), соединенные шнуром, лежат на столе. Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить к первому бруску? Трением пренебречь.
3. Два бруска массами m1=1 кг и m2=4 кг (рис. 1), соединенные шнуром, лежат на столе. Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить к первому бруску? Трением пренебречь.
Ответ: а) T=10 Н; б) T=8 Н; в) T=6 Н; г) T=12 Н; д) T=4 Н.
 4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с – 2 вокруг оси, проходящей через точку, расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с – 2 вокруг оси, проходящей через точку, расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
Ответ: а) M=4,88 Н×м; б) M=3,88 Н×м;
в) M=2,88 Н×м; г) M=1,88 Н×м; д) M=0,88 Н×м.
 5. Тонкий стержень длиной 0,5 м под действием вращающего момента M=1 Н×м вращается с угловым ускорением e=3 рад/c2, относительно оси, проходящей через точку, находящуюся на расстоянии d=0,5l (l – длина стержня) от середины стержня перпендикулярно к его длине (рис. 3). Определить массу стержня.
5. Тонкий стержень длиной 0,5 м под действием вращающего момента M=1 Н×м вращается с угловым ускорением e=3 рад/c2, относительно оси, проходящей через точку, находящуюся на расстоянии d=0,5l (l – длина стержня) от середины стержня перпендикулярно к его длине (рис. 3). Определить массу стержня.
Ответ: а) m=2 кг; б) m=3 кг; в) m=4 кг; г) m=5 кг; д) m=6 кг.
6. Какова длина математического маятника, совершающего колебания по закону x=0,04cos(2t+0,8)?
Ответ: а) l=0,45 м; б) l=1,45 м; в) l=1,95 м; г) l=2,45 м;
д) l=2,95 м.
7. Под действием силы тяжести, действующей на электромотор, консольная балка прогнулась на Dx=1 мм. При каком числе оборотов якоря электромотора в минуту может возникнуть опасность резонанса?
Ответ: а) n=746 об/мин; б) n=946 об/мин; в) n=1046 об/мин;
г) n=1146 об/мин; д) n=1246 об/мин.
Вариант № 8
1. Движения материальной точки происходит согласно уравнению x=2+t–0,5t2. Найти скорость v точки в момент времени t=2 с.
Ответ: а) v=-2 м/с; б) v=1 м/c; в) v=-1 м/с; г) v=2 м/с; д) v=-2,5 м/с.
2. Точка движется по окружности радиусом R=4 м. Закон ее движения выражается уравнением s=8-2t2. Определить момент времени t, когда нормальное ускорение аn точки равно 9 м/с2.
Ответ: а) t=1,5 с; б) t=2,5 с; в) t=0,5 с; г) t=3,5 с; д) t=4,5 с.
 3. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе (рис. 1). Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить ко второму бруску? Трением пренебречь.
3. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе (рис. 1). Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить ко второму бруску? Трением пренебречь.
Ответ: а) T=12 Н; б) T=3 Н; в) T=13 Н; г) T=5 Н; д) T=2 Н.
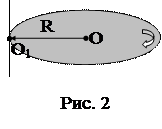 4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку, расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
4. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку, расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 2). Определить величину вращающего момента.
Ответ: а) M =0,075 Н×м; б) M=0,75 Н×м; в) M=1,75 Н×м;
г) M=2,75 Н×м; д) M=3,75 Н×м.
5. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид j=5+4t2-t3. Какова величина момента сил в момент времени, равный 2 с?
Ответ: а) M = 3,64 Н×м; б) M= -0,64 Н×м; в) M = 0,64 Н×м;
г) M = =-2,64 Н×м; д) M= -3,64 Н×м.
6. Один из двух математических маятников совершил за некоторое время n1=6 колебаний, а другой – n2=10 колебаний. Разность длин маятников Dl=16×10-2 м. Найти длины маятников ℓ1 и ℓ2.
Ответ: а) ℓ1=0,25 м, ℓ2=0,09 м; б) ℓ1=0,4 м, ℓ2=0,24 м; в) ℓ1=0,5 м, ℓ2=0,34 м; г) ℓ1=1,0 м, ℓ2=0,84 м; д) ℓ1=0,6 м; ℓ2=0,44 м.
7. Во сколько раз циклическая резонансная частота вынужденных колебаний будет больше циклической частоты собственных колебаний системы при коэффициенте затухания β=0,2w0, где w0 – циклическая частота собственных незатухающих колебаний?
Ответ: а) в 3,96 раза; б) в 2,96 раза; в) в 1,96 раза; г) в 0,96 раза; д) в 0,096 раза.
Вариант № 9
1. Уравнение движения материальной точки вдоль оси X имеет вид x=2+t-0,5t2. Найти ускорение a точки.
Ответ: а) a=2 м/с2; б) a= -2 м/с2; в) a= -1 м/с2; г) a=1 м/с2;
д) a=1,2 м/с2.
 2. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти тангенциальное ускорение точки, лежащей на поверхности вала.
2. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти тангенциальное ускорение точки, лежащей на поверхности вала.
Ответ: а) at=4 м/с2; б) at=0,04 м/с2; в) at=0,4 м/с2;
г) at=0,08 м/с2; д) at=0,8 м/с2.
3. Автомобиль весит 9,8×103 Н. Во время движения автомобиля по горизонтальной дороге на него действует сила трения, равная 0,1 его веса. Чему должна быть равна сила тяги, развиваемой двигателем автомобиля, чтобы он двигался равномерно?
Ответ: а) F=98×103 Н; б) F=9,8×103 Н; в) F=0,98×103 Н; г) F=0,98 Н; д) F=9,8×103 Н.
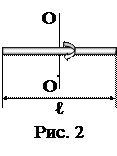 4. Тонкий стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением e=3 рад/c2 около оси, проходящей через середину стержня перпендикулярно к его длине (рис. 2). Определить величину вращающего момента M.
4. Тонкий стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением e=3 рад/c2 около оси, проходящей через середину стержня перпендикулярно к его длине (рис. 2). Определить величину вращающего момента M.
Ответ: а) М=0,025 Н×м; б) М=0,035 Н×м;
в) М=0,045 кг×м2/c2; г) М=0,055 Н×м; д) М=0,065 Н×м.
5. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид j=5+4t2-t3. Какова величина момента импульса шара в момент времени, равный 2 с?
Ответ: а) L=3,64 (кг×м2)/с; б) L=-0,64 (кг×м2)/с; в) L=0,64(кг×м2)/с; г) L=-2,64 (кг×м2)/с; д) L=-3,64 (кг×м2)/с.
6. Найти массу груза, который на пружине с жесткостью 250Н/м совершает 100 полных колебаний за 80 с.
Ответ: а) m=5 кг; б) m=4 кг; в) m=3 кг; г) m=2 кг; д) m=1 кг.
7. Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты в два раза? Коэффициенты затухания β принять равным 0,1w0, где w0 – циклическая частота собственных незатухающих колебаний.
Ответ: а) в 14,8 раза; б) в 15,8 раза; в) в 16,8 раза; г) 17,8 раза;
д) в 18,8 раза.
Вариант № 10
1. Две материальные точки движутся согласно уравнениям x1=10+t+2t2 и x2=3+2t+0,2t2. В какой момент времени скорости этих точек одинаковы?
Ответ: а) t=2 с; б) t=3 с; в) t=0,28 с; г) t= -2,8 с; д) t=2,8 с.
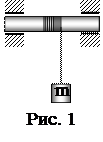 2. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти нормальное ускорение точки, лежащей на поверхности вала, в конечный момент движения.
2. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти нормальное ускорение точки, лежащей на поверхности вала, в конечный момент движения.
Ответ: а) an=16 м/с2; б) an=0,16 м/с2; в) an=1,6 м/с2;
г) an=160 м/с2; д) an=0,016 м/с2.
3. Автомобиль весит 9,8×103 Н. Во время движения автомобиля по горизонтальной дороге, на него действует сила трения, равная 0,1 его веса. Чему должна быть равна сила тяги, развиваемой двигателем автомобиля, чтобы он двигался с ускорением 2 м/с2?
Ответ: а) F=0,98∙103 Н; б) F=1,98∙103 Н; в) F=3,98∙103 Н;
г) F=2,98∙103 Н; д) F=4,98∙103 Н.

4. Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M=0,1Н×м около оси, проходящей через точку, находящуюся на расстоянии l=0,25 м от середины стержня перпендикулярно к его длине (рис. 2). Определить угловое ускорение стержня.
Ответ: а) e=7 с-2; б) e=6 с-2; в) e=5 с-2; г) e=4 с-2; д) e=3 с-2.
 5. Определить момент инерции шара, массой 10кг и радиусом 20 см (рис. 3), относительно оси, расположенной на расстоянии l=0,5R от центра шара.
5. Определить момент инерции шара, массой 10кг и радиусом 20 см (рис. 3), относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=0,5 кг×м2; б) I=0,46 кг×м2; в) I=0,36 кг×м2; г) I=0,26 кг×м2; д) I=0,16 кг×м2.
6. Уравнение колебаний пружинного маятника массой 200 г имеет вид x=0,05cos(8pt+p/3). Определить жесткость пружины, если ее массой можно пренебречь.
Ответ: а) k=1,26 Н/м; б) k=12,6 Н/м; в) k=126 Н/м; г) k=226 Н/м; д) k=326 Н/м.
7. При выступлении одного из популярных певцов в зрительном зале неожиданно зазвенели стекла окон. Определить собственную циклическую частоту стекол, если коэффициенты затухания β=0,2w0, где w0 – циклическая частота собственных незатухающих колебаний, а частота отклика n=1200 Гц.
Ответ: а) n=826 Гц; б) n=926 Гц; в) n=1026 Гц; г) n=1226 Гц;
д) n=1426 Гц.
Вариант № 11
1. Две материальные точки движутся согласно уравнениям x1=4t+8t2-16t3 и x2=2t-4t2+t3. В какой момент времени ускорения этих точек будут одинаковы?
Ответ: а) t=0,54 с; б) t=0,44 с; в) t=0,34 с; г) t=0,24 с; д) t=0,14 с.
 2. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося диска, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30о с вектором ее линейной скорости (рис. 1).
2. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося диска, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30о с вектором ее линейной скорости (рис. 1).
Ответ: а) an/at=0,5; б) an/at=0,8; в) an/at=0,68; г) an/at=0,7;
д) an/at=0,58.
3. С каким ускорением поднимается лифт, если пружинные весы с гирей в 2 кг в момент начала подъема показали 24 Н? Принять g=10м/с2.
 Ответ: а) a=1 м/с2; б) a=2 м/с2; в) a=4 м/с2; г) a=3 м/с2; д) a=2,5 м/с2.
Ответ: а) a=1 м/с2; б) a=2 м/с2; в) a=4 м/с2; г) a=3 м/с2; д) a=2,5 м/с2.
4. Тонкий стержень массой 300 г вращается с угловым ускорением e=4 рад/c2 под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии d=0,25 м от середины стержня перпендикулярно к его длине. Определить длину стержня (рис. 2).
Ответ: а) l=0,4 м; б) l=0,5 м; в) l=0,6 м; г) l=0,7 м; д) l=0,8 м.
5. Определить момент инерции медного шара радиусом R=10 см относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=5,4×10-3 кг×м2; б) I=2,4×10-3 кг×м2; в) I=3,4×10-3 кг×м2;
г) I=4,4×10-3 кг×м2; д) I=1,4×10-3 кг×м2.
6. К пружине подвешен груз массой 10 кг. Сколько колебаний может совершить этот пружинный маятник за 5 с, если под действием силы 20 Н пружина растягивается на 3 см?
Ответ: а) N=3,5; б) N=4,5; в) N=5,5; г) N=6,5; д) N=7,5.
7. Определить период колебаний математического маятника длиной l=1 м в лифте, движущемся вертикально с ускорением a=1,8м/с2, направленным вниз.
Ответ: а) T=5,2 с; б) T=4,2 с; в) T=3,2 с; г) T=2,2 с; д) T=1,2 с.
Вариант № 12
1. Две материальные точки движутся согласно уравнениям x1=4t+8t2-16t3 и x2=2t-4t2+t3. Найти скорости этих точек в момент времени, когда их ускорения одинаковы.
Ответ: а) v1=36 м/с; v2=17 м/с; б) v1=3,6 м/с; v2=17 м/с; в) v1=5,6 м/с; v2=-17 м/с; г) v1=17 м/с; v2=-39,6 м/с; д) v1=39,6 м/с; v2=-17 м/с.
2. Найти угловое ускорение колеса, если известно, что через 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α=60о с направлением линейной скорости этой точки (рис. 1).
 Ответ: а) e=44 с-2; б) e=4,4 с-2; в) e=0,044 с-2;
Ответ: а) e=44 с-2; б) e=4,4 с-2; в) e=0,044 с-2;
г) e=440 с-2; д) e=0,43 с-2.
3. Тело равномерно скользит по наклонной плоскости с углом a. Чему равен коэффициент трения f?
Ответ: а) f=sina; б) f=cosa; в) f=tga; г) f=ctga; д) f=sina×cosa.
 4. Тонкий стержень длиной 0,5 м под действием вращающего момента M=1 Н×м вращается с угловым ускорением e=3 рад/c2 относительно оси, проходящей через точку, находящуюся на расстоянии d=0,5l (l – длина стержня) от середины стержня перпендикулярно к его длине (рис. 2). Определить массу стержня.
4. Тонкий стержень длиной 0,5 м под действием вращающего момента M=1 Н×м вращается с угловым ускорением e=3 рад/c2 относительно оси, проходящей через точку, находящуюся на расстоянии d=0,5l (l – длина стержня) от середины стержня перпендикулярно к его длине (рис. 2). Определить массу стержня.
Ответ: а) m=2 кг; б) m=3 кг; в) m=4 кг; г) m=5 кг; д) m=6 кг.
5. Определить момент инерции Земли относительно оси вращения.
Ответ: а) I=20,7×1037 кг×м2; б) I=11,7×1037 кг×м2; в) I=9,7×1037 кг×м2; г) I=5,7×1037 кг×м2; д) I=3,7×1037 кг×м2.
6. Какова длина математического маятника, совершающего колебания по закону x=0,04cos(2t+0,8)?
Ответ: а) l=0,45 м; б) l=1,45 м; в) l=1,95 м; г) l=2,45 м;
д) l=2,95 м.
7. Стержень длиной 40 см колеблется около оси, перпендикулярной стержню и проходящей через один из его концов. Определить период колебаний такого маятника. Принять g=9,8 м/с2.
Ответ: а) T=0,94 с; б) T=1,04 с; в) T=1,14 с; г) T=1,24 с;
д) T=1,34 с.
Вариант № 13
1. Точка движется по окружности радиусом R=4 м. Закон ее движения выражается уравнением s=8-2t2. Определить момент времени t, когда нормальное ускорение аn точки равно 9 м/с2.
Ответ: а) t=1,5 с; б) t=2,5 с; в) t=3,5 с; г) t=4,5 с; д) t=5,5 с.
2. Стационарный искусственный спутник движется по окружности в плоскости земного экватора, оставаясь все время над одним и тем же пунктом земной поверхности. Определить угловую скорость w спутника.
Ответ: а) w=7,27∙10-5 рад/с; б) w=3∙10-5 рад/с; в) w=7 рад/с;
г) w=5,3 рад/с; д) w=4,3×10-5 рад/с.
 3. Две гири с массами m1=1 кг и m2=2 кг соединены нерастяжимой, невесомой нитью, перекинутой через невесомый блок. Найти ускорение, с которым движутся гири (рис. 1). Трением в блоке пренебречь. Принять g=9,8 м/с2.
3. Две гири с массами m1=1 кг и m2=2 кг соединены нерастяжимой, невесомой нитью, перекинутой через невесомый блок. Найти ускорение, с которым движутся гири (рис. 1). Трением в блоке пренебречь. Принять g=9,8 м/с2.
Ответ: а) а=3,27 м/с2; б) а=0,3 м/с2; в) а=9,8 м/с2;
г) а=0,98 м/с2; д) а=0,4 м/с2.
4. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид j=5+4t2-t3. Какова величина момента сил в момент времени, равный 2 с.
Ответ: а) M = 3,64 Н×м; б) M = -0,64 Н×м; в) M = 0,64 Н×м;
г) M= =-2,64 Н×м; д) M= -3,64 Н×м.
5. Определить момент импульса Земли относительно оси вращения.
Ответ: а) L = 17×1033 (кг×м2)/с; б) L = 15×1033 (кг×м2)/с;
в) L=12×1033 (кг×м2)/с; г) L=7×1033 (кг×м2)/с; д) L=3×1033 (кг×м2)/с.
6. Один из двух математических маятников совершил за некоторое время n1=6 колебаний, а другой – n2=10 колебаний. Разность длин маятников Dl=16×10-2 м. Найти длины маятников ℓ1 и ℓ2.
Ответ: а) ℓ1=0,25 м, ℓ2=0,09 м; б) ℓ1=0,4 м, ℓ2=0,24 м; в) ℓ1=0,5 м, ℓ2=0,34 м; г) ℓ1=1,0 м, ℓ2=0,84 м; д) ℓ1=0,6 м; ℓ2=0,44 м.
7. Обруч диаметром 56,6 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти частоту этих колебаний. Принять g=9,8 м/с2.
Ответ: а) n=0,96 Гц; б) n=0,76 Гц; в) n=0,66 Гц; г) n=0,56 Гц;
д) n=0,46 Гц.
Вариант № 14
 1. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти тангенциальное ускорение точки, лежащей на поверхности вала.
1. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти тангенциальное ускорение точки, лежащей на поверхности вала.
Ответ: а) at=4 м/с2; б) at=0,04 м/с2; в) at=0,4 м/с2;
г) at=0,08 м/с2; д) at=0,8 м/с2.
2. Определить нормальное ускорение точек, лежащих на земной поверхности на широте Москвы (j=58o, R3=6400 км).
Ответ: а) anМ=0,18 м/с2; б) anМ=1,8 м/с2; в) anМ=18 м/с2;
г) anМ=180 м/с2; д) anМ=0,018 м/с2.

3. Две гири с массами 2 кг и 1 кг соединены нерастяжимой, невесомой нитью, перекинутой через невесомый блок (рис. 2). Найти силу натяжения нити, действующую на гири. Трением в блоке пренебречь. Принять g=9,8 м/с2.
Ответ: а) Т= 1,31 Н; б) Т= 2,31 Н; в) Т= 23,31 Н;
г) Т= 13,1 Н; д) Т= 3,31 Н.
4. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид j=5+4t2-t3. Какова величина момента импульса шара в момент времени, равный 2 с?
Ответ: а) L=3,64 (кг×м2)/с; б) L=-0,64 (кг×м2)/с; в) L=0,64(кг×м2)/с; г) L=-2,64 (кг×м2)/с; д) L=-3,64 (кг×м2)/с.
 5. Обруч массой m=1 кг и радиусом 100 см (рис. 3) вращается относительно оси, проходящей через центр масс с угловой скоростью 100 рад/с. Определить модуль момента импульса обруча.
5. Обруч массой m=1 кг и радиусом 100 см (рис. 3) вращается относительно оси, проходящей через центр масс с угловой скоростью 100 рад/с. Определить модуль момента импульса обруча.
Ответ: а) L=150 (кг×м2)/с; б) L=80 (кг×м2)/с;
в) L=120 (кг×м2)/с; г) L=100 (кг×м2)/с; д) L=130 (кг×м2)/с.
6. Найти массу груза, который на пружине с жесткостью 250Н/м совершает 100 полных колебаний за 80 с.
Ответ: а) m=5 кг; б) m=4 кг; в) m=3 кг; г) m=2 кг; д) m=1 кг.
7. Диск радиусом 10 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний такого физического маятника. Принять g=9,8 м/с2.
Ответ: а) T=0,58 с; б) T=0,68 с; в) T=0,78 с; г) T=0,88 с;
д) T=0,98 с.
Вариант № 15
 1. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти нормальное ускорение точки, лежащей на поверхности вала, в конечный момент движения.
1. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти нормальное ускорение точки, лежащей на поверхности вала, в конечный момент движения.
Ответ: а) an=16 м/с2; б) an=0,16 м/с2; в) an=1,6 м/с2; г) an=160 м/с2; д) an=0,016 м/с2.
2. Определить линейную скорость точек, лежащих на земной поверхности на экваторе (R3=6400 км).
Ответ: а) vэ=4,65 м/с; б) vэ=46,5 м/с; в) vэ=0,465 м/с; г) vэ=465 м/с; д) vэ=4650 м/с.
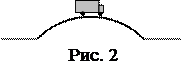 3. Радиус кривизны выпуклого моста, двигаясь по которому со скоростью 72 км/ч автомобиль не оказывает давления на мост в верхней его точке (рис. 2), равен (принять ускорение свободного падения g=10 м/с2):
3. Радиус кривизны выпуклого моста, двигаясь по которому со скоростью 72 км/ч автомобиль не оказывает давления на мост в верхней его точке (рис. 2), равен (принять ускорение свободного падения g=10 м/с2):
Ответ: а) R=50 м; б) R=100 м; в) R=40 м; г) R=120 м; д) R=60 м.

4. Определить момент инерции шара, массой 10кг и радиусом 20 см (рис. 3), относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=0,5 кг×м2; б) I=0,46 кг×м2; в) I=0,36 кг×м2; г) I=0,26 кг×м2; д) I=0,16 кг×м2.
5. Определить момента инерции обруча, массой m=1 кг и радиусом R=100 см относительно оси, перпендикулярной его плоскости, расположенной на расстоянии l=0,5R от центра (рис. 4).
 Ответ: а) I=5,25 кг×м2; б) I=4,25 кг×м2;
Ответ: а) I=5,25 кг×м2; б) I=4,25 кг×м2;
в) I=3,25 кг×м2; г) I=2,25 кг×м2; д) I=1,25 кг×м2.
6. Уравнение колебаний пружинного маятника массой 200 г имеет вид x=0,05cos(8pt+p/3). Определить жесткость пружины, если ее массой можно пренебречь.
Ответ: а) k=1,26 Н/м; б) k=12,6 Н/м; в) k=126 Н/м; г) k=226 Н/м; д) k=326 Н/м.
7. Тонкий однородный стержень длиною 60 см колеблется около горизонтальной оси, проходящей через конец стержня. Определить длину математического маятника, период колебаний которого равен периоду колебаний стержня.
Ответ: а) ℓ=1,4 м; б) ℓ=1 м; в) ℓ=0,4 м; г) ℓ=2 м; д) ℓ=0,8 м.
Вариант № 16
 1. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося диска, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30о с вектором ее линейной скорости (рис. 1).
1. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося диска, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30о с вектором ее линейной скорости (рис. 1).
Ответ: а) an/at=0,5; б) an/at=0,8; в) an/at=0,68; г) an/at=0,7;
д) an/at=0,58.
2. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=А+2t+1t3. Найти угловую скорость w через время t=2,00 с после начала движения.
 Ответ: а) w=0,14 рад/с; б) w=1,4 рад/с; в) w=24 рад/с; г) w=14 рад/с; д) w=2,4 рад/с.
Ответ: а) w=0,14 рад/с; б) w=1,4 рад/с; в) w=24 рад/с; г) w=14 рад/с; д) w=2,4 рад/с.
3. Невесомый блок укреплен на конце стола. Гири равной массы соединены нитью перекинутой через блок (рис. 2). Коэффициент трения одной из гирь о стол равен 0,1. Найти ускорение, с которым движутся гири. Трением в блоке пренебречь.
Ответ: а) а=5,1 м/с2; б) а=7,3 м/с2; в) а=9 м/с2; г) а=1,23 м/с2;
д) а=4,4 м/с2.
4. Определить момент инерции медного шара радиусом R=10 см относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=5,4×10-3 кг×м2; б) I=2,4×10-3 кг×м2; в) I=3,4×10-3 кг×м2;
г) I=4,4×10-3 кг×м2; д) I=1,4×10-3 кг×м2.
 5. Определить момента инерции алюминиевого цилиндра (рис. 3) радиусом R=100 см и высотой h=0,5 м относительно оси, перпендикулярной плоскости его оснований, расположенной на расстоянии l=0,5R от центра.
5. Определить момента инерции алюминиевого цилиндра (рис. 3) радиусом R=100 см и высотой h=0,5 м относительно оси, перпендикулярной плоскости его оснований, расположенной на расстоянии l=0,5R от центра.
Ответ: а) I=3,2×103 кг×м2; б) I=4,2×103 кг×м2;
в) I=5,2×103 кг×м2; г) I=6,2×103 кг×м2; д) I=7,2×103 кг×м2.
6. К пружине подвешен груз массой 10 кг. Сколько колебаний может совершить этот пружинный маятник за 5 с, если под действием силы 20 Н пружина растягивается на 3 см?
Ответ: а) N=3,5; б) N=4,5; в) N=5,5; г) N=6,5; д) N=7,5.
7. Физический маятник в виде тонкого кольца совершает малые колебания около оси, проходящей через одну из точек кольца перпендикулярно его плоскости. Найти длину математического маятника, обладающего тем же периодом, что и данное кольцо.
Ответ: а) ℓ=2R м; б) ℓ=3R м; в) ℓ=4 Rм; г) ℓ=5R м; д) ℓ=6R м.
Вариант № 17
 1. Найти угловое ускорение колеса, если известно, что через 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α=60о с направлением линейной скорости этой точки (рис. 1).
1. Найти угловое ускорение колеса, если известно, что через 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α=60о с направлением линейной скорости этой точки (рис. 1).
Ответ: а) e=44 с-2; б) e=4,4 с-2; в) e=0,044 с-2;
г) e=440 с-2; д) e=0,43 с-2.
2. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=А+2t+t3. Найти угловое ускорение e в момент времени t=0,5 c.
Ответ: а) e=3 рад/с2; б) e=1 рад/с2; в) e=2 рад/с2; г) e=0,3 рад/с2; д) e=0,03 рад/с2.
 3. Невесомый блок укреплен на конце стола. Гири равной массы по 1 кг каждая соединены нитью перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 2). Найти силу натяжения нити. Трением в блоке пренебречь.
3. Невесомый блок укреплен на конце стола. Гири равной массы по 1 кг каждая соединены нитью перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 2). Найти силу натяжения нити. Трением в блоке пренебречь.
Ответ: а) Т=5,4 Н; б) Т=1,8 Н; в) Т= – 2,8 Н; г) Т=3,8 Н; д) Т=2,8 Н.
4. Определить момент инерции Земли относительно оси вращения.
Ответ: а) I=20,7×1037 кг×м2; б) I=11,7×1037 кг×м2; в) I=9,7×1037 кг×м2; г) I=5,7×1037 кг×м2; д) I=3,7×1037 кг×м2.
 5. Свинцовый цилиндр радиусом 10 см высотой h=0,2 м вращается относительно оси, проходящей через центр масс перпендикулярной основанию цилиндра (рис. 3), с угловой скоростью 100 рад/с. Определить модуль момента импульса такого цилиндра.
5. Свинцовый цилиндр радиусом 10 см высотой h=0,2 м вращается относительно оси, проходящей через центр масс перпендикулярной основанию цилиндра (рис. 3), с угловой скоростью 100 рад/с. Определить модуль момента импульса такого цилиндра.
Ответ: а) L=1,55 (кг×м2)/с; б) L=15,5 (кг×м2)/с; в) L=25,5 (кг×м2)/с; г) L=35,5 (кг×м2)/с; д) L=45,5 (кг×м2)/с.
6. Стержень длиной 40 см колеблется около оси, перпендикулярной стержню и проходящей через один из его концов. Определить период колебаний такого маятника. Принять g=9,8 м/с2.
Ответ: а) T=0,94 с; б) T=1,04 с; в) T=1,14 с; г) T=1,24 с;
д) T=1,34 с.
7. Логарифмический декремент затухания маятника l=0,003. Определить число N полных колебаний, которые должен совершить маятник, чтобы амплитуда уменьшилась в два раза.
Ответ: а) N=91; б) N=121; в) N=151; г) N=191; д) N=231.
Вариант № 18
1. Стационарный искусственный спутник движется по окружности в плоскости земного экватора, оставаясь, все время над одним и тем же пунктом земной поверхности. Определить угловую скорость w спутника.
Ответ: а) w=7,27∙10-5 рад/с; б) w=3∙10-5 рад/с; в) w=7 рад/с;
г) w=5,3 рад/с; д) w=4,3×10-5 рад/с.
2. Диск радиусом 0,1 м вращается согласно уравнению j=10+20t - 2t2. Определить по величине тангенциальное ускорение точек на окружности диска.
Ответ: а) at=0,4 м/с2; б) at=-4 м/с2; в) at=-0,8 м/с2; г) at=0,8 м/с2;
д) at=-0,4 м/с2.
 3. Маховик радиусом 0,2 м и массой 1 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно 14,7 Н (рис. 1). Какое число оборотов в секунду будет делать маховик через 1 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
3. Маховик радиусом 0,2 м и массой 1 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно 14,7 Н (рис. 1). Какое число оборотов в секунду будет делать маховик через 1 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
Ответ: а) n=2,67 об/с; б) n=5,67 об/с; в) n=10,67 об/с;
г) n=18,67об/с; д) n=23,4 об/с.
4. Определить момент импульса Земли относительно оси вращения.
Ответ: а) L = 17×1033 (кг×м2)/с; б) L = 15×1033 (кг×м2)/с;
в) L=12×1033 (кг×м2)/с; г) L=7×1033 (кг×м2)/с; д) L=3×1033 (кг×м2)/с.

5. Определить момента инерции алюминиевого цилиндра радиусом R=0,10 м и высотой h=0,50 м относительно оси, перпендикулярной плоскости его оснований, расположенной на расстоянии l=2R от центра (рис. 2).
Ответ: а) I=2,9 кг×м2; б) I=1,9 кг×м2;
в) I=0,9 кг×м2; г) I=0,19 кг×м2; д) I=0,29 кг×м2.
6. Обруч диаметром 56,6 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти частоту этих колебаний. Принять g=9,8 м/с2.
Ответ: а) n=0,96 Гц; б) n=0,76 Гц; в) n=0,66 Гц; г) n=0,56 Гц;
д) n=0,46 Гц.
7. Чему равен логарифмический декремент колебаний математического маятника, если за 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника равна 1 м.
Ответ: а) l=2,3; б) l=1,3; в) l=0,23; г) l=0,23; д) l=0,023.
Вариант № 19
1. Определить нормальное ускорение точек, лежащих на земной поверхности на широте Москвы (j=58o, R3=6400 км).
Ответ: а) anМ=0,18 м/с2; б) anМ=1,8 м/с2; в) anМ=18 м/с2;
г) anМ=180 м/с2; д) anМ=0,018 м/с2.
2. Диск радиусом 0,1 м вращается согласно уравнению j=10+20t–2t2. Определить по величине нормальное ускорение точек на окружности диска для момента времени t=4с.
 Ответ: а) an=1,6 м/с2; б) an=2,6 м/с2; в) an=0,6 м/с2; г) an=16 м/с2; д) an=0,16 м/с2.
Ответ: а) an=1,6 м/с2; б) an=2,6 м/с2; в) an=0,6 м/с2; г) an=16 м/с2; д) an=0,16 м/с2.
3. Две гири разного веса соединены нитью, перекинутой через блок, момент инерции которого 50 кг×м2 и радиус 0,2 м. Блок вращается с трением и момент сил трения равен 98,1 Н×м (рис. 1). Найти разность натяжения нитей по обе стороны блока, если известно, что он вращается с постоянным угловым ускорением 2,36рад/с2.
Ответ: а) ΔТ=2,68×103 Н; б) ΔТ=5,68×103 Н;
в) ΔТ=1,68×103 Н; г) ΔТ=1,08×103 Н; д) ΔТ=3,68×103 Н.

4. Обруч массой m=1 кг и радиусом 100 см (рис. 2) вращается относительно оси, проходящей через центр масс с угловой скоростью 100 рад/с. Определить модуль момента импульса обруча.
Ответ: а) L=150 (кг×м2)/с; б) L=120 (кг×м2)/с; в) L=110 (кг×м2)/с; г) L=100 (кг×м2)/с; д) L=90 (кг×м2)/с.
5. Маховое колесо начинает вращаться с угловым ускорением e=0,5 рад/с2 и через время t=15 с после начала движения приобретает момент импульса L=73,5 (кг×м2)/с. Определить момент инерции махового колеса.
Ответ: а) I=9,8 кг×м2; б) I=7,2 кг×м2; в) I=5,8 кг×м2; г) I=6,2 кг×м2; д) I=2,2 кг×м2.
6. Диск радиусом 10 см колеблется около горизонтальной оси, про