Главная | Обратная связь

Квантовая природа излучения

5.1. Объяснить, почему в неотапливаемом помещении температура всех тел одинакова.

5.2. Объяснить, почему открытые окна домов со стороны улиц ка­жутся черными.

5.3. Чайная фарфоровая чашка на светлом фоне имеет темный рису­нок. Объяснить, почему если эту чашку быстро вынуть из печи, где она нагревалась до высокой температуры, и рассматривать в темноте, то наблюдается светлый рисунок на темном фоне.

5.4. Имеется два одинаковых алюминиевых чайника, в которых до одной и той же температуры нагрето одинаковое количество воды. Один чайник закопчен, а другой – чистый. Объяснить, ка­кой из чайников остынет быстрее и почему.

5.5. Определить, во сколько раз необходимо уменьшить термодина­мическую температуру черного тела, чтобы его энергетическая светимость R_э ослабилась в 16 раз. Ответ: В 2 раза.

5.6. Температура внутренней поверхности муфельной печи при от­крытом отверстии площадью 30 см² равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт. Ответ: 0,676.

5.7. Энергетическая светимость черного тела R_э = 10 кВт/м². Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела. Ответ: 4,47 мкм.

5.8. Определить, как и во сколько раз изменится мощность излуче­ния черного тела, если длина волны, соответствующая макси­муму его спектральной плотности энергетической светимости, сместилась с λ₁ = 720 нм до λ₂ = 400 нм. Ответ: Увеличится в 10,5 раза.

5.9. Черное тело находится при температуре T₁ = 3 кК. При остыва­нии тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на Δλ = 8 мкм. Определить температуру Т₂, до которой тело охлади­лось. Ответ: 323 К.

5.10. Черное тело нагрели от температуры T₁ = 600 К до Т₂ = 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) как изменилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости. Ответ: 1) в 256 раз; 2) уменьшилась на 3,62 мкм.

5.11. Площадь, ограниченная графиком спектральной плотности энергетической светимости r_λT черного тела, при переходе от термодинамической температуры Т₁ к температуре Т₂ увеличилась в 5 раз. Определить, как изменится при этом длина волны λ_max, соответствующая максимуму спектральной плотности энергетической светимости черного тела. Ответ: Уменьшится в 1,49 раза.

5.12. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилась с λ₁ = 2,7 мкм до λ₂ = 0,9 мкм. Определить, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает согласно закону r_λT = СТ⁵,

где С = 1,3^.10^-5 Вт/(м^3.К⁵). Ответ: 1) в 81 раз; 2) в 243 раза.

5.13. Определить, какая длина волны соответствует максимальной спектральной плотности энергетической светимости (r_λT)_max, равной 1,3^.10¹¹ (Вт/м²)/м (см. задачу 5.12). Ответ: 1,83 мкм.

5.14. Считая никель черным телом, определить мощность, необходимую для поддержания температуры расплавленного никеля 1453 °С неизменной, если площадь его поверхности равна 0,5 см². Потерями энергии пренебречь. Ответ: 25,2 Вт.

5.15. Металлическая поверхность площадью S = 15 см², нагретая до температуры Т = 3000 К, излучает в одну минуту 100 кДж. Опре­делить: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверх­ности и черного тела при данной температуре. Ответ: 1) 413 кДж; 2) 0,242.

5.16. Принимая Солнце за черное тело, и учитывая, что его макси­мальной спектральной плотности энергетической светимости соответствует длина волны λ = 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения. Ответ: 1) 5800 К; 2) 2,34^.10²⁹ Дж; 3) 2,6^.10¹² кг.

5.17. Определить температуру тела, при которой оно при температуре окружающей среды t₀ = 23 °С излучало энергии в 10 раз больше, чем поглощало. Ответ: 533 К.

5.18. Считая, что тепловые потери обусловлены только излучением, определить, какую мощность необходимо подводить к медному шарику диаметром d = 2 см, чтобы при температуре окружающей среды t₀ = -13 °С поддерживать его температуру равной t = 17 °C. Принять поглощательную способность меди А_T = 0,6. Ответ: 0,107 Вт.

5.19. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d = 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t = 2800 °С. Поверхность проволоки принять в качестве серой с поглощательной способностью А_T = 0,343. Удельное сопротивление проволоки при данной температуре ρ = 0,92^.10^-4 Ом^.см. Температура окружающей проволоку среды t₀ = 17 °C. Ответ: 48,8 А.

5.20. Преобразовать формулу Планка для спектральной плотности энергетической светимости черного тела от переменной ν к переменной λ.

5.21. Используя формулу Планка, определить спектральную плотность потока излучения единицы поверхности черного тела, приходящегося на узкий интервал длин волн Δλ = 5 нм около максимума спектральной плотности энергетической светимости, если температура черного тела Т = 2500 К. Ответ: r_λTΔλ = 6,26 кВт/м².

5.22. Объяснить: 1) происхождение радиационной, цветовой и ярко­стной температур; 2) может ли радиационная температура быть больше истинной.

5.23. Для вольфрамовой нити при температуре Т = 3500 К поглощательная способность А_T = 0,35. Определить радиационную темпе­ратуру нити. Ответ: 2,69 кК.

5.24. Отношение энергетической светимости R^C_T серого тела к энергетической светимости R_Э черного тела равно A_T. Вывести связь между истинной и радиационной температурами. Ответ: Т = T_p / .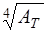

5.25. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U₀ = 3,7 В. Ответ: 1,14 Мм/с.

5.26. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект. Ответ: 2,48 эВ.

5.27. Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения U₀ = 3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света ν₀ = 6^.10¹⁴ с^-1. Опреде­лить: 1) работу выхода электронов из этого металла; 2) частоту применяемого облучения. Ответ:1) 2,48 эВ; 2) 1,32^.10¹⁵ с^-1.

5.28. Определить работу выхода А электронов из вольфрама, если «красная граница» фотоэффекта для него λ₀ = 275 нм. Ответ: 4,52 эВ.

5.29. Калий освещается монохроматическим светом с длиной волны 400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ. Ответ: 0,91 В.

5.30. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом с длиной волны 400 нм. Ответ:1) 2,48 эВ; 2) 468 км/с.

5.31. Выбиваемые светом при фотоэффекте электроны при облучении фотокатода видимым светом полностью задерживаются обратным напряжением U₀ = l,2 B. Специальные измерения показали, что длина волны падающего света λ = 400 нм. Определить «красную границу» фотоэффекта. Ответ: 652 нм.

5.32. Задерживающее напряжение для платиновой пластинки (работа выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для другой пластинки задерживающее напряжение равно 5,3 В. Определить работу выхода электронов из этой пластинки. Ответ: 4,7 эВ.

5.33. Определить, до какого потенциала зарядится уединенный серебряный шарик при облучении его ультрафиолетовым светом длиной волны λ = 280 нм. Работа выхода электронов из серебра А = 4,7 эВ. Ответ: 1,27 В.

5.34. При освещении вакуумного фотоэлемента монохроматическим светом с длиной волны λ₁ = 0,4 мкм он заряжается до разности потенциалов φ₁ = 2 В. Определить, до какой разности потенциа­лов зарядится фотоэлемент при освещении его монохроматиче­ским светом с длиной волны λ₂ = 0,3 мкм. Ответ: 3,04 В.

5.35. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны λ = 83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью Е = 10 В/см. «Красная граница» фотоэффекта для серебра λ₀ = 264 нм. Ответ: 1,03 см.

5.36. Фотоны с энергией ε = 5 эВ вырывают фотоэлектроны из металла с работой выхода А = 4,7 эВ. Определить максимальный импульс, передаваемый поверхности этого металла при вылете электрона. Ответ: 2,96^.10^-25 кг^.м/с.

5.37. При освещении катода вакуумного фотоэлемента монохроматическим светом с длиной волны λ = 310 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25 % задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим экспериментальным данным постоянную Планка. Ответ: 6.61^.10^-34 Дж^.с.

5.38. Определить максимальную скорость υ_maxфотоэлектронов, вырываемых с поверхности цинка (работа выхода А = 4 эВ), при облучении γ-излучением с длиной волны λ = 2,47 пм. Ответ: 259 Мм/с.

5.39. Определить для фотона с длиной волны λ = 0,5 мкм: 1) его энергию; 2) импульс; 3) массу. Ответ: 1) 2,48 эВ; 2) 1,33^.10^-27 кг^.м/с; 3) 4,43^.10^-36 кг.

5.40. Определить энергию фотона, при которой его масса равна массе покоя электрона. Ответ выразить в электрон-вольтах. Ответ: 0,512 МэВ.

5.41. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона, длина волны ко­торого λ = 0,5 мкм. Ответ: 1,45 км/с.

5.42. Определить длину волны фотона, импульс которого равен импульсу электрона, прошедшего разность потенциалов U = 9,8 В. Ответ: 392 пм.

5.43. Определить температуру, при которой средняя энергия молекул трехатомного газа равна энергии фотонов, соответствующих из­лучению λ = 600 нм. Ответ: 8 кК.

5.44. Определить, с какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона, длина волны которого λ = 0,5 мкм. Ответ: 934 км/с.

5.45. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона, длина волны ко­торого λ = 2 пм. Ответ: 0,77 с.

5.46. Доказать, что световое давление, оказываемое на поверхность тела потоком монохроматического излучения, падающего пер­пендикулярно поверхности, в случае идеального зеркала равно 2w, а в случае полностью поглощающей поверхности равно w, где w – объемная плотность энергии излучения.

5.47. Давление монохроматического света с длиной волны λ = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фо­тонов, падающих ежесекундно на 1 м² поверхности. Ответ: 9,05^.10⁹.

5.48. На идеально отражающую поверхность площадью S = 5 см² за время t = 3 мин нормально падает монохроматический свет, энергия которого W = 9 Дж. Определить: 1) облученность поверхности; 2) световое давление, оказываемое на поверхность. Ответ: 1) 100 Вт/м²; 2) 667 нПа.

5.49. Определить давление света на стенки электрической 150-ваттной лампочки, принимая, что вся потребляемая мощность идет на излучение и стенки лампочки отражают 15 % падающего на них света. Считать лампочку сферическим сосудом радиуса 4 см. Ответ: 28,6 мкПа.

5.50. Давление монохроматического света с длиной волны λ = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, равно 0,15 мкПа. Определить число фотонов, падающих на поверхность площадью 40 см² за одну секунду. Ответ: 4,52^.10¹⁷.

5.51. Давление Р монохроматического света с длиной волны λ = 600 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, составляет 0,1 мкПа. Определить: 1) концентрацию n фотонов в световом пучке; 2) число N фотонов, падающих ежесекундно на 1 м² поверхности. Ответ: 1) 3,02^.10¹¹ м^-3, 2) 9,06^.10¹⁹.

5.52. На идеально отражающую плоскую поверхность нормально падает монохроматический свет с длиной волны λ = 0,55 мкм. Поток излучения Ф_есоставляет 0,45 Вт. Определить: 1) число фотонов N, падающих на поверхность за время t = 3 с; 2) силу давления, испытываемую этой поверхностью. Ответ: 1) 4,15^.10¹⁸; 2) 3 нН.

5.53. Плоская световая волна интенсивностью I = 0,1 Вт/см² падает под углом α = 30° на плоскую отражающую поверхность с коэффициентом отражения ρ = 0,7. Используя квантовые представления, определить нормальное давление, оказываемое светом на эту поверхность. Ответ: 4,25 мкПа.

5.54. Рассматривая особенности механизма комптоновского рассея­ния, объяснить: 1) почему длина волны рассеянного излучения больше, чем длина волны падающего излучения; 2) наличие в составе рассеянного излучения «несмещенной» линии.

5.55. Определить длину волны рентгеновского излучения, если при комптоновском рассеянии этого излучения под углом Θ = 60° длина волны рассеянного излучения оказалась равной 57 пм. Ответ: 56,9 пм.

5.56. Фотон с энергией ε = 1,025 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной комптоновской длине волны λ_с = 2,43 пм. Ответ: 60°.

5.57. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Оказывается, что длины волн рассеянного под углами Θ₁ = 60° и Θ₂ = 120° излучения отлича­ются в 1,5 раза. Определить длину волны падающего излучения, предполагая, что рассеяние происходит на свободных электро­нах. Ответ: 3,64 пм.

5.58. Фотон с длиной волны λ = 5 пм испытал комптоновское рассеяние под углом Θ = 90° на первоначально покоившемся свободном электроне. Определить: 1) изменение длины волны при рассеянии; 2) энергию электрона отдачи; 3) импульс электрона отдачи. Ответ: 1) 2,43 пм; 2) 81,3 кэВ; 3) 1,6^.10^-22 кг^.м/с.

5.59. Фотон с энергией ε = 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20 %. Ответ: 41,7 кэВ.

5.60. Фотон с энергией 0,3 МэВ рассеялся под углом Θ = 180° на свободном электроне. Определить долю энергии фотона, прихо­дящуюся на рассеянный фотон. Ответ: 0,461.

5.61. Фотон с энергией 100 кэВ в результате комптоновского эффекта рассеялся при соударении со свободным электроном на угол Θ = π/2. Определить энергию фотона после рассеяния. От­вет: 87,3 кэВ.

5.62. Фотон с энергией ε = 0,25 МэВ рассеялся под углом α = 120° на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи. Ответ: 106 кэВ.