Главная | Обратная связь

Запишем распределение Бозе-Эйнштейна и выражение для внутренней энергии идеального фононного газа

,
, (3)
где и суммирование ведется по всем фононным состояниям. Для вычисления энергии надо знать спектр частот кристаллической решетки . Его нахождение представляет нетривиальную задачу даже для сравнительно простых решеток.

Используем для расчета внутренней энергии и теплоемкости кристалла так называемую непрерывную модель. Кроме этого, предположим, что скорости всех упругих волн одинаковы. Такое предположение не вполне корректно, но оно позволяет упростить вычисления и получить основные результаты. В результате оказывается, что спектральная плотность фононных орбиталей 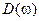отличается от фотонной плотнос­ти множителем 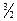(у фотона две поляризации, у фонона – три). Поэтому, для фононов

.
и формула (3) переходит в интеграл

. (4)
Верхний предел интегрирования в (4) равен дебаевской частоте , а не бесконечен, как в случае фотонов. В теории Дебая она определяется соотношением

.
В итоге получаем

.

Введем в (4) новую переменную интегрирования 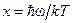и определим характеристическую температуру Дебая формулой . Тогда выражение для внутренней энергии примет вид

. (5)

При высоких температурах формула (5) приводится к виду

.
В этом случае в согласии с законом Дюлонга и Пти.

При низких температурах верхний предел интегрирования в (5) можно положить равным бесконечности (соответствующее значение интеграла равно ). В результате получаем для энергии

,
для теплоемкости

. (6)
Этот результат известен как закон Дебая.

Вырожденный электронный газ в металле. Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми-Дирака. Рассмотрим вначале электронный ферми-газ при температуре абсолютного нуля – полностью вырожденный ферми-газ. При распределение электронов по состояниям ведет себя как ступенчатая функция

(7)
В формуле (7) величина – предельное значение химического потенциала при , а – ступенчатая функция. Физический смысл (7) очевиден. При 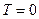фермионы заполняют самые низкие энергетические уровни. По принципу Паули каждое состояние может быть занято только одним электроном. Поэтому уровни до 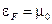при 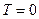являются занятыми, причем для этих уровней , а вышележащие уровни свободны . Максимальная энергия электронов , равная предельному значению химического потенциала, называется энергией Ферми.

В импульсном пространстве электроны также заполняют все состояния с импульсами от нуля до максимального импульса 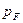. Число квантовых состояний в интервале импульсов от p до p+dp равно , где множитель 2 учитывает кратность спинового вырождения. Число электронов с импульсами от нуля до максимального импульса 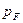равно

.
Отсюда для граничного импульса – импульса Ферми – имеем

( – концентрация электронов проводимости), а для энергии Ферми находим

.
Наконец, полная энергия газа равна

.
Согласно уравнению состояния идеального газа находим давление ферми-газа при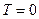

.
Таким образом, даже при температуре абсолютного нуля давление электронного газа отлично от нуля. Для 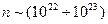см^–3 имеем атм. Это обстояте­льство является следствием того, что электроны не находятся в покое даже при .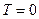

При температурах, отличных от нуля, часть электронов переходит с уровней, лежащих ниже уровня Ферми , на уровни, лежащие выше этой границы. В результате ступенька расплывается и превращается в пунктирную линию (рис.). Из формулы распределения Ферми-Дирака легко видеть, что полуширина распределения . Поэтому температуру естественно назвать температурой вырождения электронного газа (ступенька полностью расплывается). При более высоких температурах вырождение снимается, – электронный газ ведет себя как классический. Численная оценка приводит к значению К. Следовательно, электронный газ в металлах при любых температурах вплоть до точки плавления остается вырожденным.