 |
|
Ряди Фур’є в гільбертових просторах
Векторний простір 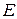 називається евклідовим простором (ЕП) (над полем
називається евклідовим простором (ЕП) (над полем  ), якщо в ньому визначена функція скалярний добуток (СД)
), якщо в ньому визначена функція скалярний добуток (СД)  , який задовольняє наступним аксіомам:
, який задовольняє наступним аксіомам:
1. 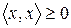 ,
,  ;
;
2. 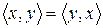 ;
;
3. 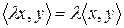 ;
;
4. 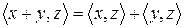 .
.
Лема 1. (Визначення норми в ЕП)
В ЕП 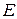 можна визначити норму за формулою:
можна визначити норму за формулою:
 . (1)
. (1)
При цьому норма називається узгодженою із СД. В подальшому будемо вважати, що якщо заданий ЕП, то норма в ньому узгоджена із СД.
Лема 2. (Неперервність СД)
СД в ЕП є неперервною на  функцією.
функцією.
Обидві леми були доведені в темі ФБЗ.
Вектори 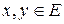 називаються ортогональними, якщо
називаються ортогональними, якщо  . Сім’я векторів
. Сім’я векторів 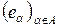 називається ортогональною, якщо
називається ортогональною, якщо 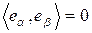
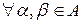 ,
,  . Сім’я векторів називається ортонормованою (ОНСВ), якщо вона ортогональна і при цьому
. Сім’я векторів називається ортонормованою (ОНСВ), якщо вона ортогональна і при цьому 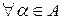
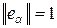 .
.
Теорема 1. (Ортогональність основної тригонометричної системи)
Нехай 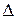 - інтервал довжини
- інтервал довжини  і
і 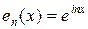

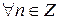 . Тоді сім’я векторів
. Тоді сім’я векторів  ортогональна в евклідовому просторі
ортогональна в евклідовому просторі  .
.
Доведення. Нагадаємо, що скалярний добуток в просторі  визначається за формулою:
визначається за формулою:
 (2)
(2)
Нехай 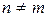 , тоді
, тоді 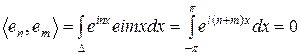 .
.
Теорема доведена.
Наслідок 1. (Ортонормованість основної тригонометричної системи)
Сім’я векторів 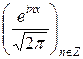 ОНСВ в просторі
ОНСВ в просторі  .
.
Для доведення достатньо обчислити норму елемента: 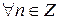
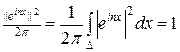 .
.
Наслідок 2. (Ортонормована тригонометрична система)
Нехай  , тоді сім’я векторів
, тоді сім’я векторів 
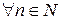 ,
, 
 є ОНСВ в просторі
є ОНСВ в просторі  .
.
Гільбертовим простором (ГП)  називається ЕП, що є повним у нормі, що узгоджена із скалярним добутком.
називається ЕП, що є повним у нормі, що узгоджена із скалярним добутком.
Теорема 2. (Фішера-Рісса про повноту простору)
Простір  , де
, де 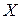 - обмежений проміжок дійсної осі, є гільбертовим.
- обмежений проміжок дійсної осі, є гільбертовим.
Без доведення.
Нехай  - ГП. Ряд
- ГП. Ряд 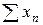 в цьому просторі називається збіжним (збіжним до елемента
в цьому просторі називається збіжним (збіжним до елемента  ), якщо збігається послідовність
), якщо збігається послідовність 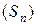 (якщо послідовність
(якщо послідовність  , тобто
, тобто 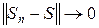 при
при 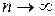 ), де
), де 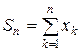 - послідовність часткових сум.
- послідовність часткових сум.
Теорема 3. (Критерій збіжності ортогонального ряду)
Ортогональний ряд 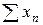 (тобто ряд, члени якого утворюють ортогональну систему) елементів ГП
(тобто ряд, члени якого утворюють ортогональну систему) елементів ГП  збігається тоді і тільки тоді, коли:
збігається тоді і тільки тоді, коли:
 . (3)
. (3)
Доведення. Оскільки 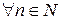
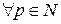

 ,
,
а далі твердження випливає з повноти просторів  та
та  .
.
Теорема доведена.
Нехай 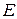 - ЕП, ряд
- ЕП, ряд 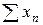 елементів цього простору називається безумовно збіжним, якщо для будь-якої бієкції
елементів цього простору називається безумовно збіжним, якщо для будь-якої бієкції 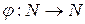 збігається ряд
збігається ряд  .
.
Теорема 4. (Критерій безумовної збіжності ортогонального ряду)
Ортогональний ряд 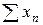 елементів ГП
елементів ГП  безумовно збігається тоді і тільки тоді, коли виконується умова (3).
безумовно збігається тоді і тільки тоді, коли виконується умова (3).
Доведення. Оскільки для будь-якої бієкції 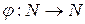 ряд
ряд  є ортогональним і
є ортогональним і  і все випливає з теореми 3.
і все випливає з теореми 3.
Теорема доведена.
Нехай зафіксовано ОНСВ 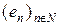 у ГП
у ГП  .
.
Теорема 5. (Коефіцієнти збіжного ряду)
Якщо ряд 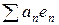 збігається і
збігається і  , то:
, то:

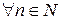 . (4)
. (4)
Доведення. Внаслідок неперервності СД маємо:
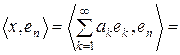
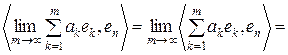
 .
.
Теорема доведена.
Ряд 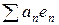 , що побудований для заданої ОНСВ
, що побудований для заданої ОНСВ 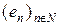 ГП
ГП  , коефіцієнти якого обчислюються за формулами (4) називається рядом Фур’є елемента
, коефіцієнти якого обчислюються за формулами (4) називається рядом Фур’є елемента 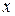 (РФ) по ОНСВ
(РФ) по ОНСВ 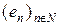 .
.
З теореми 5 слідує, що будь-який збіжний в ГП  ряд по ОНСВ
ряд по ОНСВ 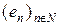 є РФ своєї суми, але це не виключає, що він є РФ іншого елемента
є РФ своєї суми, але це не виключає, що він є РФ іншого елемента 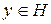 та не збігається до
та не збігається до 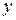 .
.
Теорема 6. (Нерівність Бесселя)
Нехай 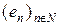 ОНСВ у ГП
ОНСВ у ГП  . Тоді
. Тоді  справджується нерівність Бесселя:
справджується нерівність Бесселя:
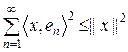 . (5)
. (5)
Доведення. Нехай  . Тоді згідно з властивостями СД та нерівності Шварца маємо:
. Тоді згідно з властивостями СД та нерівності Шварца маємо:

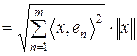

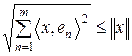 ,
,
яке виконується 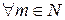 , що і є рівносильним нерівності Бесселя (5).
, що і є рівносильним нерівності Бесселя (5).
Теорема доведена.
Теорема 7. (Про збіжність РФ)
Кожен РФ по ОНСВ збігається у ГП (але не обов’язково до відповідного елемента).
Доведення слідує з теореми 3 та нерівності Бесселя.
Теорема 8. (Про збіжність ортогонального ряду)
Ортогональний ряд в ГП збігається тоді і тільки тоді, коли він є РФ деякого елемента.
Доведення слідує з теорем 5 і 7.
Теорема 9. (Фішера-Рісса про збіжність ряду)
Нехай 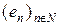 - ОНСВ в ГП
- ОНСВ в ГП  . Якщо для послідовності
. Якщо для послідовності 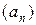 збігається ряд
збігається ряд  , то існує такий елемент
, то існує такий елемент 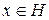 , що
, що 
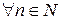 .
.
Доведення. З теореми 3 ряд 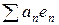 збігається в просторі
збігається в просторі  . За теоремою 5 він є РФ своєї суми.
. За теоремою 5 він є РФ своєї суми.
Теорема доведена.
Теорема 10. (Рівність Парсеваля-Стєклова)
РФ елемента 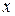 по ОНСВ
по ОНСВ 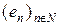 у ГП
у ГП  збігається до вектора
збігається до вектора 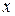 тоді і тільки тоді, коли справджується рівність Парсеваля-Стєклова:
тоді і тільки тоді, коли справджується рівність Парсеваля-Стєклова:
 . (6)
. (6)
Доведення одержимо с тотожності:
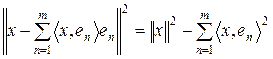 ,
, 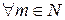 . (7)
. (7)
Наслідок. (Рівність Парсеваля-Стєклова для тригонометричної системи)
Для тригонометричних РФ рівність Парсеваля-Стєклова набуває вигляду:
 , (8)
, (8)
або ж, враховуючи показникові форму запису коефіцієнтів Фур’є, тобто  , рівність набуває вигляду:
, рівність набуває вигляду:
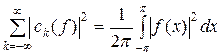 . (9)
. (9)
Сім’я векторів 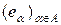 ГП
ГП  називається повною, якщо не існує ненульового вектора
називається повною, якщо не існує ненульового вектора 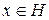 :
: 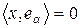
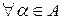 .
.
Сім’я векторів 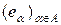 ГП
ГП  називається замкненою, якщо
називається замкненою, якщо 
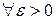
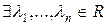
 :
:
 . (10)
. (10)
Теорема 11. (Зв’язок повноти та замкненості системи)
Для ОНСВ 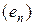 ГП
ГП  наступні умови рівносильні:
наступні умови рівносильні:
1) Система векторів 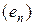 замкнена в
замкнена в  ;
;
2) Система векторів 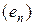 повна в
повна в  ;
;
3)  РФ елемента
РФ елемента 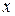 має суму, яка дорівнює
має суму, яка дорівнює 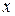 ;
;
4)  виконується рівність Парсеваля-Стєклова.
виконується рівність Парсеваля-Стєклова.
Доведення проведемо за схемою 4)  3)
3)  1)
1)  2)
2)  3).
3).
4)  3) доведено в теоремі 10.
3) доведено в теоремі 10.
3)  1) слідує з означення замкненої системи.
1) слідує з означення замкненої системи.
1)  2) нехай
2) нехай 

 внаслідок лінійності та неперервності СД елемент
внаслідок лінійності та неперервності СД елемент 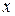 ортогональний замиканню лінійної оболонки системи векторів
ортогональний замиканню лінійної оболонки системи векторів 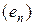 , яке згідно означення збігається з
, яке згідно означення збігається з  , отже
, отже 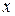 ортогональний і собі
ортогональний і собі 
 .
.
2)  3)
3)  , нехай РФ
, нехай РФ 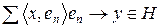 , а тому він є РФ елемента
, а тому він є РФ елемента 





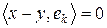

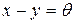

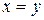 .
.
Теорема доведена.
Нехай  – ГП,
– ГП, 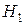 – множина його векторів, що задовольняє умови:
– множина його векторів, що задовольняє умови:
1) 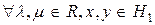

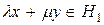 ;
;
2) 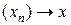 ,
, 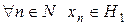

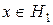 ;
;
тоді множина 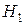 називається підпростором.
називається підпростором.
Вектор 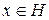 називається ортогональним підпростору
називається ортогональним підпростору 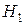 , якщо
, якщо 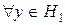
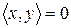 , будемо це записувати
, будемо це записувати  .
.
Теорема 12. (Ортогональність вектору підпростору)
Нехай 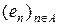
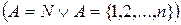 повна ОНСВ
повна ОНСВ 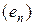 у ГП
у ГП  і
і  . Вектор
. Вектор 

 .
.
Доведення. Необхідність. 
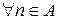


 .
.
Достатність.  і
і 

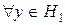 виконується рівність:
виконується рівність: 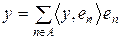

 .
.
Теорема доведена.
Нехай 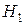 - підпростір ГП
- підпростір ГП  . Вектор
. Вектор  називається ортогональною проекцією елемента
називається ортогональною проекцією елемента 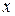 на
на 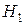 , якщо
, якщо 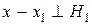 .
.
Теорема 13. (Про ортогональну проекцію)
Нехай 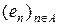
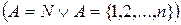 повна ОНСВ
повна ОНСВ 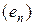 у ГП
у ГП  і
і  . Тоді існує єдина ортогональна проекція
. Тоді існує єдина ортогональна проекція 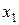 вектора
вектора 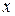 на підпростір
на підпростір 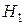 і справджується формула:
і справджується формула:
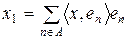 . (11)
. (11)
Доведення. Якщо виконується (11), то 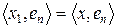
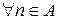 , а тому
, а тому 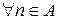
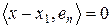 , що й означає ортогональність
, що й означає ортогональність 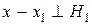 . Доведемо від супротивного, що вона єдина:
. Доведемо від супротивного, що вона єдина: 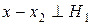

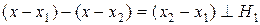 і при цьому
і при цьому 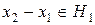

 .
.
Теорема доведена.
Нехай  – довільний ГП. Упорядкований набір векторів
– довільний ГП. Упорядкований набір векторів  простору
простору  називається орієнтованим трикутником, якщо
називається орієнтованим трикутником, якщо 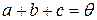 . Вектори
. Вектори  називаються його сторонами. Трикутник називається прямокутним, якщо в нього існують дві ортогональні сторони, що називаються катетами, третя сторона називається гіпотенузою.
називаються його сторонами. Трикутник називається прямокутним, якщо в нього існують дві ортогональні сторони, що називаються катетами, третя сторона називається гіпотенузою.
Теорема 14. (Піфагора)
Якщо  – катети, а
– катети, а 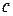 – гіпотенуза прямокутного трикутника, то
– гіпотенуза прямокутного трикутника, то
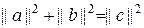 . (12)
. (12)
Для доведення достатньо піднести до квадрату рівність  .
.
Наслідок. (Довжина катету та гіпотенузи)
У будь-якому прямокутному трикутнику довжина катету менша за довжину гіпотенузи.
Нехай 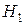 – підпростір ГП
– підпростір ГП  ,
, 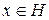 . Число
. Число 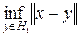 називається найкращим наближенням вектора
називається найкращим наближенням вектора 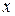 за допомогою векторів простору
за допомогою векторів простору 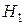 .
.
Теорема 15. (Про найкраще наближення)
Нехай 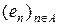
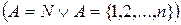 повна ОНСВ
повна ОНСВ 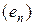 у ГП
у ГП  і
і  . Тоді сума Фур’є
. Тоді сума Фур’є 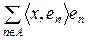 здійснює найкраще наближення вектора
здійснює найкраще наближення вектора 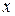 за допомогою векторів з
за допомогою векторів з 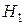 , тобто
, тобто
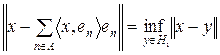 . (13)
. (13)
При цьому
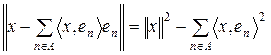 . (14)
. (14)
Доведення. Нехай 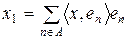 - сума Фур’є, розглянемо трикутник
- сума Фур’є, розглянемо трикутник  . За теоремою 13
. За теоремою 13 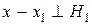 , а
, а 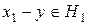

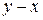 - гіпотенуза цього трикутника
- гіпотенуза цього трикутника  з наслідку з теореми Піфагора виконується (13). Застосувавши саму теорему Піфагора до трикутника
з наслідку з теореми Піфагора виконується (13). Застосувавши саму теорему Піфагора до трикутника 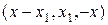 одержимо (14).
одержимо (14).
Теорема доведена.