 |
|
Распространение света в проводящих средах.
При рассмотрении вопроса применения электромагнитной теории Максвелла к данному случаю, задача сводится к учету проводимости металла, т.е. формально к введению в уравнения Максвелла членов, зависящих от коэффициента электропроводности . 
Отражение света от поверхности металла, как и его распространение в нем, может быть рассмотрено на основе материальных уравнений, в которых диэлектрическая проницаемость () комплексна. Соответственно показатель преломления n – тоже комплексный: 
. (4.96)
В сильно поглощающих средах и металлах мнимая часть преобладает над вещественной. Частичное проникновение света в металл создает токи проводимости. С ними связано выделение джоулевой теплоты, т.е. поглощение света – необратимое превращение электромагнитной энергии в энергию хаотического теплового движения. Чем выше проводимость металла, тем меньшая доля падающего света проникает в металл и поглощается там. В идеальном проводнике, которому формально соответствует 
, потери на джоулеву теплоту вообще отсутствуют, так что падающий свет полностью отражается.
Пусть из вакуума на металл падает плоская монохроматическая волна с волновым вектором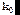 
(рис.4.14); 
– волновой вектор отраженной волны. Во второй среде волна неоднородна и 
.(4.97)Тогда, как и при выводе формул Френеля:
.(4.98)
Видно, что составляющая вектора k2 , направленная вдоль границы вещественна. Поэтому мнимая часть вектора k2 перпендикулярна поверхности металла. Это значит, что плоскости равных амплитуд прошедшей волны параллельны границе раздела. Вектор 
перпендикулярен плоскостям постоянных фаз и характеризует направление прошедшей волны. Угол называется вещественным углом преломления. Отношение 
зависит от угла падения (в отличие от диэлектриков).
Формулы Френеля остаются в силе, если в них рассматривать cos2 как комплексную величину: 
(4.99)
Знак корня нужно взять так, чтобы неоднородная волна затухала вглубь металла. Тогда коэффициенты отражения тоже комплексны:
(4.100)
В общем случае 
. При линейной поляризации падающего света с произвольным азимутом в отраженной волне появляется сдвиг фаз, приводящий к эллиптической поляризации отраженного света. Отраженный свет остается линейно поляризованным, если
1) падающий свет s– или p–поляризован;
2) 
;
3) 
.
При нормальном падении: 
(4.101)
. (4.102)
У металлов 2 значительно больше другого слагаемого. Поэтому 
(см. таблицу для желтой части спектра).
| Металл | n | ||
| Na | 0,97 | 0,044 | 2,42 |
| Ag | 0,94 | 0,20 | 3,44 |
| Cd | 0,84 | 1,13 | 5,01 |
| Al | 0,83 | 1,44 | 5,23 |
| Au | 0,82 | 0,47 | 2,83 |
| Hg | 0,77 | 1,60 | 4,80 |
| Cu | 0,71 | 0,62 | 2,57 |
| Pb | 0,54 | 3,46 | 3,25 |
| Fe | 0,33 | 1,51 | 1,63 |
Волновой вектор прошедшей в металл волны при нормальном падении имеет только z – составляющую:
; (4.103)
— глубина проникновения.(4.104)
При достаточно высоких частотах роль «силы трения» в уравнениях колебаний электрона (см. раздел по дисперсии) становится несущественной. Случай = 0 формально соответствует «идеальному» металлу с .При 
, а 
. (4.105)
В этом случае из (4.102) следует = 1, т.е. отражение от поверхности идеального проводника полное.Закон Бугера. Для затухающей волны, распространяющейся вдоль оси Z, интенсивность излучения:
. (4.106)
Отсюда получаем зависимость: 
, (4.107)
называемая законом Бугера, где – линейный показатель поглощения. Другой вид закона Бугера (см. (4.104)):
, (4.108)
где 0 – длина волны света в вакууме.
17 Уравнение эйконала. Запишем волновое уравнение для световой волны в среде с коэффициентом преломления n=c/v:
(5.1)
В общем случае для монохроматической волны справедливо: 
(5.2)
Подставляя (5.2) в (5.1) находим уравнение для амплитуды (r), зависящей только от координаты:
(5.3)
где k0=/c – волновое число в вакууме. Волновое число в среде k=nk0. Воспользуемся соотношением (для других координат будет аналогично):
(5.4)
Тогда (5.3) после деления на преобразуется к виду:
(5.5)
Решение этого уравнения ищем в виде:
(5.6)
Вещественная скалярная функция S(r) называется эйконалом(от греческого eikon – изображение). Подставляя (5.6) в (5.5), получаем:
(5.7)
Приравнивая нулю вещественную и мнимую части, получим два уравнения для определения А(r) и S(r):
(5.8)
Для оптического диапазона длина волны много меньше расстояния L, на которых амплитуда волны существенно меняется (порядка размера оптических элементов). Поэтому первыми двумя слагаемыми в первом уравнении (5.8) можно пренебречь (их сумма имеет порядок 1/L2). Тогда это уравнение в оптическом диапазоне принимает вид:
(5.9)
Это уравнение называется уравнением эйконала.
Градиент от функции S(r) направлен по нормали к поверхности S=const. Поэтому эйконал S описывает поверхности постоянной фазы волны, а S приводит к понятию луча, т.е. к представлению о движении световой энергии в данной точке в определенном направлении. Лучом называется линия, касательная к которой совпадает в каждой точке с вектором S. Распространение света рассматривается как движение световой энергии по лучам. Плоскость, перпендикулярная лучам света (где S = const), называется волновым фронтом.
Анализ распространения света в лучевом приближении составляет предмет геометрической оптики. Этот подход оправдан всегда, когда
. (5.10)
Физически этот член описывает искривление материальными объектами световых лучей, т.е. дифракцию света. Исходя из этого, можно сказать, что в геометрической оптике не учитываются дифракционные эффекты (см. гл.7).
Принцип Ферма.В однородной среде S=kЧr (k=const) и лучи являются прямыми параллельными линиями, а фронт волны – плоскостью, перпендикулярной лучам.
Для неоднородной среды лучи имеют более сложную конфигурацию. Пусть точки P1 и P2 соединяются лучом L (рис.5.1). Вычислим изменение фазы вдоль луча. Для каждой его точки имеем:
(5.11)
где dr направлен по лучу и совпадает с S, dl – элемент длины пути. Для изменения фазы находим:
(5.12)
Интегрирование идет вдоль луча. Интеграл в (5.12) называется оптической длиной пути. Из (5.12) следует, что оптические длины путей вдоль различных лучей между точками волнового фронта в два момента времени одинаковы. Для любой другой кривой, соединяющей точки P1 и P2 , оптическая длина пути оказывается больше, чем для реального луча.
Принцип Ферма (Fermat Pierre, 1601 – 1675) утверждает, что интеграл в (5.12) вдоль луча имеет стационарное значение, т.е. первая вариация S относительно соседних путей интегрирования равна нулю. Или то же самое в другой формулировке: реальный луч отличается от остальных кривых, соединяющих две заданные точки, тем, что соответствующая ему оптическая длина имеет стационарное значение, т.е. малое изменение траектории не приводит к изменению оптической длины.
К принципу Ферма можно подойти и с другой стороны. Учтем что dt=dl / v – время прохождения пути dl со скоростью v, а n(r) = c / v(r). Тогда
(5.13)
где интеграл здесь дает время, затрачиваемое на прохождение пути от P1 и P2. С этой точки зрения принцип Ферма звучит так: лучом, соединяющим две точки, является тот путь, который делает стационарным время, затрачиваемое светом на его прохождение. Формулировка о стационарности времени прохождения пути между двумя точками, с одной стороны, утверждает экстремальный характер этого времени, а с другой стороны, не исключает наличия нескольких путей с одинаковым временем прохождения.
Например, в геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и то же время на прохождение своего пути. Другими словами, оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы (принцип таутохронизма).
18 Вывод закона преломления из принципа Ферма.Пусть требуется соединить лучом две точки P1 и P2 , находящиеся в однородных средах с коэффициентами преломления n1 и n2, разделенных плоской границей (рис. 5.2). В каждой однородной среде луч – прямая линия. Из геометрии рисунка получаем для полного времени распространения света между точками P1 и P2:
(5.14)
Условие стационарности 
принимает вид:
(5.15)
Учитывая, что 
получаем соотношение , полностью совпадающее с законом Снеллиуса: 
(5.16)
Распространение луча в среде с переменным коэффициентом преломления.Пусть свет распространяется в среде с аксиально-симметричным изменением коэффициента преломления. Луч распространяется вдоль положительного направления этой оси Z в параксиальном приближении. Расстояние от оси – r. Из закона Снеллиуса для бесконечно тонкого слоя r имеем:
(5.17)
Разложим n(r + r) в ряд Тейлора и ограничимся линейным по r членом:
(5.18)
В параксиальном приближении sin; cos1. Тогда с учетом линейного приближения получаем:
(5.19)
Т.к. tg1 = r / z , то в параксиальном приближении:
(5.20)
С учетом (5.20) из (5.19) находим уравнение распространения луча:
(5.21)
Например для диэлектрического волоконного световода n(r)=n0(1– ar2/2)и ar2/2«1(a>0). Тогда уравнение (5.21) принимает вид: d2r/dz2 = – ar. Общее решение этого уравнения гармонических колебаний в пространстве хорошо известно. Это значит, что луч внутри такого световода имеет синусоидальную траекторию.
19Прохождение лучей в центрированных оптических системах.Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину (рис.5.3). Обозначения видны из рисунка.
Ось Z совпадает с осью линзы. Главной оптической осью линзыназывается прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r1 и r2 – радиусы кривизны 1-й и 2-й сферических поверхностей линзы (r2 на рис.5.3 не показан, чтобы не загромождать рисунок). Весь расчет проводится в параксиальном приближении: 
(5.22)
Преломление на первой сферической поверхности.В точке P1 закон Снеллиуса в параксиальном приближении имеет вид:
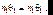(5.23)
Используя геометрические соотношения между углами: 
(5.24)
а в параксиальном приближении
(5.25)
из (5.23) получаем:
(5.26)
Кроме этого учтем соотношение 
(5.27)
Система уравнений (5.26) и (5.27) позволяют, задав координаты падающего на первую поверхность линзы луча (n11 ; x1), найти координаты (n1/1/ ; x1/) преломленного в линзе луча. Полученную систему удобно записать в матричном виде:
(5.28)
где величина k1=(n1/–n1)/r1 называется преломляющей силой первой поверхности, а матрица
(5.29)
называется преломляющей матрицей первой поверхности.
Распространение луча внутри линзы.Преломленный луч в параксиальном приближении, пройдя внутри линзы, падает на её вторую поверхность на расстоянии x2 от оси:
(5.30)
Отметим, что величина в параксиальном приближении практически равна толщине линзы А1А2 . С учетом, что 
получаем в матричном виде:
(5.31)
Матрица 
(5.32)
описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей.
Преломление луча на второй сферической поверхностирассматривается точно так же, как и на первой поверхности. Величина k2=(n2/ –n2)/r2 называется преломляющей силой второй поверхности, а матрица R2 – преломляющей матрицей второй поверхности:
(5.33)
Знаки всех величин в приведенных выражениях необходимо брать с учётом правила знаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы , отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис. 5.3 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны.
Распространение луча через оптическую систему.Используя (5.29), (5.31), (5.33), получаем связь между характеристиками на выходе линзы и входе в неё:
(5.34)
(5.35)
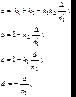(5.36)
где a, b, c, d называются постоянными Гаусса. Независимыми являются только три из четырех постоянных Гаусса. Матрица S21 полностью описывает рассмотренную оптическую систему.
Преобразование луча от плоскости предмета к плоскости изображения.Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А1 выходит луч с координатами (n11, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А2 на расстоянии l/ луч характеризуется координатами (n2/2/, x/). Между этими парами координат по приведенным выше правилам получаем соотношение:
(5.37)
(Знак l уже учтён)Перемножая матрицы в (5.37), имеем:
(5.38)
Матрица Q21 называется матрицей преобразования предмета к изображению:
(5.39)
Обозначим 
(5.40)
– увеличение оптической системы. Введем понятие изображения. Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением.
Исходя из этого определения в точке изображения увеличение М не должно зависеть от угла 1. Поэтому соответствующий член в матрице Q21 обращается в нуль:
(5.41)
Из определения увеличения и выражения (5.40) имеем:
(5.42)
Тогда матрица преобразования от предмета к изображению принимает вид:
(5.43)
20 Кардинальные элементы оптической системы.Плоскости H и H/, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (ось Z) – главными точками системы. Найдём из (5.42) их положение:
(5.44)
где lH – отсчёт положения плоскости H относительно точки А1; lH/ – отсчёт положения плоскости H относительно точки А2 . Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (5.42) их положение:
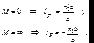(5.45)
где lF – отсчёт положения переднего фокуса относительно точки А1 , lF/ – отсчёт положения заднего фокуса относительно точки А2 Расстояние f между передним фокусом и передней главной точкой называется передним фокусным расстоянием; расстояние f /между задним фокусом и задней главной точкой называется задним фокусным расстоянием:
(5.46)
Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис). Физический смысл постоянных Гаусса.Пусть линза располагается в воздухе: n1 = n2/ = 1. Тогда из (5.46) следует:
(5.47)
т.е. a является величиной, обратной фокусному расстоянию. Из (5.45) и (5.47) имеем:
(5.48)
Коэффициенты b и c характеризуют взаимное расположение главных и фокальных плоскостей.
Уравнение линзы.Из подобия треугольников CDF, ABC, FPA (рис.5.4) следует:
(5.49)
а из подобия треугольников A/D/F/, F/H/C/, A/B/C/ следует:
(5.50)
Из этих соотношений имеем:
(5.51)
а отсюда получаем уравнение линзы в форме Ньютона:
(5.52)
Из этих же уравнений можно получить уравнение линзы в форме Гаусса:
(5.53)
Увеличение линзы определяется из формулы:
(5.54)
21 Тонкие линзы.Пусть 
– относительный коэффициент преломления и 
. Тогда из (5.36) и (5.47) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
(5.55)
Тонкой линзой называется линза, для которых можно пренебречь третьим слагаемым в скобках (5.55), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:
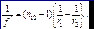(5.56)
Тонкая линза представляется не имеющей толщины и с ней совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:
(5.57)
Величина 
(5.58)
называется оптической силой линзы. Оптическая сила измеряется в диоптриях ( 1 дптр соответствует фокусному расстоянию в 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 5.5). Тогда матрица S (5.34), описывающая данную систему будет получаться из результата перемножения матриц:
(5.59)
Далее находятся постоянные Гаусса, а из них кардинальные элементы данной оптической системы. Отсчет для передних главной точки и фокуса идет от передней динзы, а для задних кардинальных точек – от последней линзы по приведенному выше правилу знаков.
Отражение от сферических поверхностейрассматривается как преломление в среду с отрицательным показателем преломления –n, если n – показатель преломления среды, из которой луч падает на отражающую поверхность. В остальном матрица, описывающая отражение, полностью аналогична матрице, описывающей преломление. Правило знаков остается тем же.
22 Аберрации оптических систем.В определении понятия изображения содержится требование того, чтобы все лучи, выходящие из точки предмета, сходились в одной и той же точке в плоскости изображения, при этом увеличение для всех точек предмета остается постоянным. Отклонения фактически получаемого изображения от идеального, описываемого всеми предыдущими формулами, называются аберрациями. Для параксиальных лучей аберрации малы и ими пренебрегают. Если же лучи не параксиальны, то аберрации становятся значительными и сильно искажают изображение.
Первый источник аберраций состоит в том, что линзы, ограниченные сферическими поверхностями, преломляют лучи не совсем так, как это принимается в параксиальном приближении (например, фокусы для лучей, падающих на разных расстояниях от оси линзы, различны.). Такие аберрации называются геометрическими. Например, параксиальное приближение основывается на линейном разложении синуса в ряд. Неучтенные в таком приближении члены 3, 5 и т.д. приводят к аберрациям третьего, пятого и т.д. порядков.К геометрическим аберрациям относятся:
1. Сферическая аберрация.
2. Кома.
3. Астигматизм.
4. Искривление поверхности изображения (кривизна поля).
5. Дисторсия.
При сферической аберрации лучи, параллельные оптической оси, не пересекаются после линзы в одной точке. Пучок параллельных оси лучей после преломления образует совокупность конусов, вершины которых расположены на оси. Огибающая эту совокупность конусов поверхность называется каустической, а сечение этой поверхности любой плоскостью, проходящей через луч – каустической кривой (рис.).
Если светящаяся точка расположена не на оптической оси, то её изображение не является светящимся кружком, как в предыдущем случае, а представляется в виде довольно сложной асимметричной фигуры, напоминающей комету с хвостом. Такая аберрация называется комой.
Если на линзу падает цилиндрический пучок лучей под достаточно большим углом к оптической оси, то в результате сечение пучка лучей изменяется с расстоянием от линзы после преломления (рис.5.7). На некотором расстоянии от линзы сечение является отрезком линии, перпендикулярным плоскости падения пучка (такая плоскость падения, образованная осью падения пучка и оптической осью, называется меридианальной плоскостью, а перпендикулярная ей – сагиттальной). Затем эта линия переходит в эллипс, на некотором расстоянии дальше сечение опять становится круговым, а затем эллиптическим и дальше превращается в отрезок линии, лежащей в меридианальной плоскости. Такой вид аберрации называется астигматизмом.
Поверхности, на которых лежат фокусы (где образуются отрезки линий при астигматизме), создаваемые меридианальной и сагиттальной фокусировками, не совпадают между собой и не являются плоскостями. Эти поверхности касаются лишь в точке F/ оптической оси. Этот вид аберрации называется искривлениемповерхностиизображения.
Увеличение системы, вообще говоря, зависит от угла наклона падающих лучей. В результате, например, сетка из прямых линий превращается в сетку из кривых линий. Такая аберрация называется дисторсией (рис.5.8).
Второй источник аберраций связан с дисперсией света. Т.к. показатель преломления зависит от частоты, то и фокусное расстояние и другие характеристики системы зависят от частоты. Поэтому лучи, соответствующие излучению различной частоты, исходящие из одной точки предмета, не сходятся в одной точке изображения даже в идеальном случае. Такие аберрации называются хроматическими.
23 Некоторые приборы геометрической оптики.
1. Глаз.(рис.5.9)
Фокусировка глаза на предмет называется аккомодацией. Средние характеристики человеческого глаза:
Оптическая сила 58 дптр.
Длина глаза 22 мм.
Радиус кривизны сетчатки 9,7 мм;
преломляющей оверхности 5,6 мм.
Показатель преломления среды 1,33;
хрусталика 1,4 – 1,45.
Расстояние наилучшего зрения 25 см.
2. Линзовый телескоп (рис.5.10). Увеличение 
(5.60)
3. Лупа . Простейшая оптическая система с малым фокусным расстоянием (1 см или немного больше). Предмет располагается на расстоянии от лупы меньше фокусного. Изображение мнимое, прямое, увеличенное. Увеличение
(5.61)
где D – расстояние наилучшего зрения (25 см).
4. Микроскоп.Передняя собирающая линза называется объективом (f1 около сантиметра), задняя – окуляром (f2 около нескольких сантиметров). Объектив строит увеличенное перевернутое действительное изображение, окуляр играет роль лупы для этого изображения как предмета. Увеличение
(5.62)
где d – расстояние между фокусами объектива и окуляра.
24Под интерференцией света обычно понимают широкий круг явлений, в которых при наложении световых волн результирующая интенсивность не равна сумме интенсивностей отдельных волн: в одних местах она больше, в других – меньше, т.е. возникают чередующиеся светлые и темные участки – интерференционные полосы. Другими словами, интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн. В дальнейшем под интенсивностью световой монохроматической волны будем понимать следующую величину, определяемую формулой:
(6.1)
где E0 – действительная амплитуда световой волны.Рассмотрим суперпозицию двух линейно поляризованных в одном направлении волн с различными амплитудами:
(6.2)
Тогда суммарная интенсивность I будет равна:
(6.3)
С учетом (6.1) и (6.2) выражение (6.3) принимает вид:
(6.4)
где 
Если частоты интерферирующих волн различны, то формула (6.4) примет вид:
. (6.5)
Последнее слагаемое в (6.4) или в (6.5) называется интерференционным членом. В тех случаях, когда он обращается в нуль, результирующая интенсивность равна сумме интенсивностей отдельных волн и интерференция отсутствует. Если же интерференционный член отличен от нуля, то суммарная интенсивность изменяется от минимального значения 
(6.6)
до максимального значения 
(6.7)
Монохроматических волн в природе не существует, поэтому приходится ограничиться квазимонохроматическими волнами. Картина интерференции монохроматических волн является лишь первым приближением в интерференции волн от реальных источников. Существующие экспериментальные методы получения интерференционной картины обычно делятся на два класса: 1) способы деления амплитуды волны; 2) способы деления фронта волны.Рассмотрим несколько примеров. Интерферометр Майкельсона. Интерферометр состоит из делительной пластинки P и двух зеркал R1и R2 , расположенных на расстояниях l1 и l1 от пластины (рис.6.1). На пластинке P происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения. Нетрудно показать, что при любом коэффициенте отражения света от пластинки амплитуды полей, приходящих в точку наблюдения А одинаковы. Т.к. частоты также остаются постоянными, то (6.5) принимает вид:
. (6.8)
При этом интенсивность I изменяется от своего минимального значения при 
до своего максимального значения при 
. Значение разности фаз определяется длинами плеч интерферометра l1 и l2 : 
. (6.9)
Пример применения интерферометра Майкельсона. При движении одного из зеркал за счет продольного эффекта Доплера происходит смещение частоты отраженной волны:
. (6.10)
Тогда существенной станет не постоянная амплитуда, а периодически изменяющаяся с частотой в соответствии со значением скорости движения зеркала:
(6.11)
Как видно, интерферометр Майкельсона – прекрасный инструмент не только для измерений расстояний, но и скорости перемещения объектов, т.к. он весьма чувствителен к перемещениям.
Поставив в одно из плеч призму или линзу, можно получить великолепный инструмент для исследования их качества по интерференционной картине (интерферометр Тваймана–Грина).
Другой пример интерферометра по методу деления амплитуды – интерферометр Маха–Цендера (рис.6.2). По изменению интерференционной картины и длине пути светового пучка в ячейке Q можно с большой точностью определить относительный показатель преломления исследуемого вещества ячейки.
26 Опыт Юнга. (1801 г.) Рассмотрим интерференцию, возникающую в результате выделения с помощью двух щелей S1и S2 участков сферического волнового фронта волны от точечного источника S (рис.6.3) (метод деления волнового фронта). Найдем разность хода лучей в произвольной точке наблюдения P на экране:
. (6.12)
При 
(что обычно реализуется в эксперименте) получаем:
. (6.13)
Следовательно, с точностью до величины первого порядка по 
имеем: 
. (6.14)
Разность фаз между волнами в точке наблюдения при этом равна:
. (6.15)
Интерференционная картина на экране в зависимости от координаты y принимает вид:
(6.16)
Расстояние на экране наблюдения между соседними максимумами или минимумами интенсивности называется шириной интерференционной полосы. Для схемы Юнга ширина полосы определяется по формуле:
(6.17)
и не зависит от порядка интерференции, являясь постоянной при заданных l, d и . Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты. Примеры экспериментальных интерференционных схем, осуществляющих метод деления волнового фронта: бипризма Френеля, билинза Бийе, бизеркало Френеля, зеркало Ллойда. Интерференция при белом свете. Каждая волна со своей длиной в данной схеме создает свою систему интерференционных полос, причем центральный максимум (при y = 0) имеет вид белой полосы, т.к. он совпадает для всех длин волн. Первые минимумы (первые темные полосы) для всех длин волн очень близки и не перекрываются с полосами высших порядков. Следующие интерференционные полосы окрашены, т.к. эти максимумы для разных длин волн разнесены в пространстве (в данном случае по y). При дальнейшем увеличении порядка интерференции интерференционная картина постепенно пропадает, т.к. дальние полосы накладываются друг на друга и смазываются.
29 Интерференция в тонких пленках. При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина волны, т.к. ее частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления:
. (6.28)
Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме.
а) Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h 
(рис.6.7). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности или в фокальной плоскости F линзы Л. С учетом потери полволны на границе раздела сред (если n > 1, то в точке A, если n < 1, то в точке B) оптическая разность хода в данном случае равна
. (6.29)
Из геометрии рисунка (вывести самостоятельно !) получаем для оптической разности хода:
. (6.30)
Условием максимума интерференционной картины по-прежнему является
. (6.31)
а условием минимума –
(6.32)
Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями.Даже если источник света протяженный и различные его точки излучают некогерентно, то интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка A на рис. 6.7) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором.
Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии). Немонохроматичность ухудшает видность интерференционной картины. С другой стороны, увеличение толщины пластины уменьшает дисперсионную область. Для наблюдения интерференции в белом свете толщина должна быть достаточно малой (~ 10 мкм). Поэтому в данном случае речь идет об интерференции в тонких пленках.
б) Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.6.8). В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке C и высчитывается по той же формуле, что и (6.30). Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Ограничения на толщину клиновидной пластины, связанные со степенью когерентности (или монохроматичности) такие же, как и в случае плоскопараллельной пластины.
Кольца Ньютона. Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот) (рис.6.9). В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина. Пусть h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы. Найдем радиус темного интерференционного кольца m-го порядка. Из геометрии рисунка видно, что 
. Учитывая, что 
, получаем 
. Используя условие минимума (6.32), получаем для радиуса m-го темного кольца:
. (6.33)
Интерференционные кольца наблюдаются как в отраженном, так и в прошедшем свете. При этом там, где в отраженном свете наблюдается светлое кольцо, то в прошедшем – темное, т.е. интерференционные картины в прошедшем и отраженном свете являются взаимно дополнительными. Центральное пятно в отраженном свете – темное, т.к. толщина воздушного клина пренебрежительно мала и волны интерферируют практически в противофазе из-за потери полволны. В белом свете, как и следует из формулы (6.33), наблюдаются цветные кольца.
Контрастность интерференционных картин в отраженном и прошедшем свете неодинакова. Для наблюдения четкой интерференционной картины в отраженном свете поверхности клина должны обладать малым коэффициентом отражения, а в прошедшем – большим. Это легко видеть из соотношений амплитуд интерферирующих волн, которые для лучшей видимости должны стремиться к единице. Для отраженных волн оно равно 
, а для прошедших – 
, где – энергетический коэффициент отражения (проверить самостоятельно).
27 Многолучевая интерференция. До сих пор мы рассматривали интерференцию между двумя волнами. Теперь рассмотрим многолучевую интерференцию на примере интерферометра Фабри–Перо (ИФП) (рис.6.10). Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим 
– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,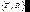 
– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
(6.34)
где и – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения и преломления достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода между соседними интерферирующими волнами на выходе пластины равна
, (6.35)
а разность фаз равна
. (6.36)
Запаздывание последующей волны относительно предыдущей за счет прохождения волны в пластинке учтем множителем е-i. Суммарная амплитуда E2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
. (6.37)
Интенсивность света определяется следующим образом:
или
(6.38)
Эта формула носит название формулы Эйри.
Отметим, что аналогично можно найти суммарную интенсивность света при отражении от плоскопараллельной пластинки:
.(6.39)
Интерференционные картины в проходящем и отраженном свете оказываются дополнительными.
Вид функции Эйри (6.38) для трех различных коэффициентов отражения (1 – =0,04; 2 – =0,4; 3 – =0,8) представлен на рис.6.11. Максимумы функции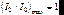 
достигаются при 
, где m = 0,1,2, ..., а минимумы 
– при 
. Т.о. функция видности интерференционной картины равна:
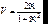,(6.40)
т.е. при 1 V 1. При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
Если на ИФП падают пучки света под всевозможными углами, то интерференционные полосы имеют вид колец. Максимальный порядок интерференции соответствует центру интерференционной картины. Интерференционная картина имеет одинаковый вид там, где падающие пучки имеют одинаковый угол падения на ИФП (полосы равного наклона). Интерференционная картина наблюдается или на бесконечности, или (что обычно реализуется в эксперименте) в фокальной плоскости линзы.
В реальных измерительных ИФП интерференция возникает между двумя отполированными с высокой точностью ( ~ 0,01) плоскими строго параллельными (с плоскостностью до 0,005) зеркалами с большими коэффициентами отражения (алюминиевые зеркала – ~75%, посеребренные – ~90%, диэлектрические интерференционные – до 99,9%). Интерферометр с показателем преломления между зеркалами n = 1 называется эталоном Фабри–Перо).