 |
|
Ортогональность сферических функций
Присоединенные функции Лежандра
Вернемся к уравнению (49) §7:
(61)
Произведем в нем подстановку
(62)
Тогда функция y будет удовлетворять уравнению
(63)
Чтобы найти его решение, продифференцируем уравнение Лежандра (50) из параграфа 7:
m раз по ς, тогда получим:
(64)
Сравнивая это уравнение с уравнением (62), можно убедиться, что функция
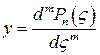
является частным решением уравнения (63). Возвращаясь к подстановке (62), мы увидим, что функции
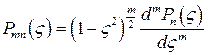(65)
будут частными решениями уравнения (61). Переходя к прежней переменной θ, мы получим искомые (частные) решения уравнения (формула 48, §7), к которому пришли при решении трехмерного уравнения Лапласа методом разделения переменных, а именно
Эти решения имеют вид
(66)
Так как полиномы Лежандра 
представляют собой полиномы степени n от cos θ, то и функции 
(которые являются производными от полиномов) также являются полиномами, причем
при 
Функции получили название присоединенных функций Лежандра или присоединенных полиномов Лежандра. Как всякие полиномы они непрерывны и дифференцируемы неограниченное число раз.
Таким образом, для каждого n мы получили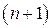 
частных решений уравнения (48) (так как 
). Комбинируя эти решения с решениями (47) уравнения (46), мы получим сферические функции (сколько?):
, 
, 
(67)
( 
, 
),
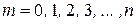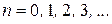являющиеся решениями уравнения (44). Эти сферические функции линейно независимы, так как линейно независимы множители 
и 
. В результате любую сферическую функцию порядка n можно представить в следующем виде:
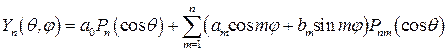(68)
Ортогональность сферических функций
Построенные в предыдущем параграфе сферические функции ортогональны на поверхности S любого шара радиуса r0с центром в начале координат, т.е. интегралы от произведения двух различных функций (68) по поверхности S равен нулю.
Покажем это для сферических функций разных порядков. Пусть 
и 
( 
) – две такие функции. Функци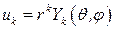и
и 
гармоничны в любой ограниченной окрестности начала координат. Действительно, они удовлетворяют уравнению Лапласа, а раз так, то по формуле Грина
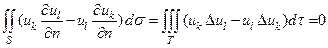
В нашем случае дифференцирование по нормали совпадает с дифференцированием по r, поэтому
,
а так как , то
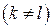
Для сферических функций одного порядка интеграл по поверхности S можно представить в виде повторного интеграла по φ в промежутке (0, 2π) и по θ в промежутке (0, π). Но в функциях одного порядка угол φ входит посредством сомножителей
образующих ортогональную систему в промежутке (0, 2π), интеграл в этих пределах от произведения любой пары из этих функций равен нулю. Следовательно, равен нулю и весь повторный интеграл, и интеграл по поверхности S.
Нормы сферических функций задаются выражениями
, (69)
(70)
Замечание(без доказательства).
Пусть функция f (θ, φ) имеет ограниченное изменение* на шаровой поверхности S. Тогда в точках непрерывности она может быть разложена в равномерно сходящийся ряд по сферическим функциям:
(71)
Для этого каждую из сферических функций надо представить в виде линейной формы (68) предыдущего параграфа
и подставив в соотношение (71), получим
(72)