 |
|
Лінійні неперервні оператори
Нехай  - лінійні нормовані простори. Відображення
- лінійні нормовані простори. Відображення 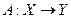 називається оператором. Оператор
називається оператором. Оператор 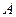 називається лінійним, якщо для будь-яких чисел
називається лінійним, якщо для будь-яких чисел  і будь-яких елементів
і будь-яких елементів  виконується рівність
виконується рівність  .
.
Оператор 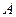 називається неперервним в точці
називається неперервним в точці  , якщо
, якщо 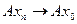 при
при  .
.
Теорема. Якщо лінійний оператор 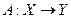 неперервний в точці
неперервний в точці 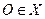 , тоді він неперервний в будь-якій точці
, тоді він неперервний в будь-якій точці 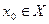 .
.
Лінійний оператор 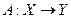 називається неперервним, якщо він неперервний в точці
називається неперервним, якщо він неперервний в точці 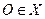 .
.
Лінійний оператор 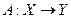 називається обмеженим, якщо
називається обмеженим, якщо 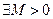 , що для будь-якого елемента
, що для будь-якого елемента  виконується нерівність
виконується нерівність  .
.
Теорема. Лінійний оператор 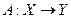 непевний тоді і тільки тоді, коли він обмежений.
непевний тоді і тільки тоді, коли він обмежений.
Нормою лінійного обмеженого оператора 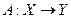 називається число
називається число
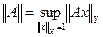 (1)
(1)
Приклад 1. Перевірити лінійність, обмеженість оператора А: 
 ,
,  і знайти його норму.
і знайти його норму.
Розв’язування. Для будь-яких дійсних чисел  і будь-яких послідовностей
і будь-яких послідовностей 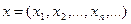 ,
,  є
є  маємо
маємо

Значить, оператор 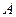 є лінійним.
є лінійним.
Перевіримо обмеженість оператора. Нехай  – довільний елемент простору
– довільний елемент простору  , тоді
, тоді

Звідки випливає обмеженість оператора і оцінка його норми 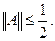
Припустимо, що існує елемент  є
є  ,
,  , для якого
, для якого  . Тоді
. Тоді  . Рівність виконується при
. Рівність виконується при 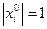 і
і  для
для  . Візьмемо елемент
. Візьмемо елемент  Він належить простору
Він належить простору  , має одиничну норму і
, має одиничну норму і  . Отже, норма оператора
. Отже, норма оператора 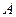 дорівнює
дорівнює 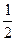 .
.
Приклад. Перевірити лінійність, обмеженість оператора  ,
,
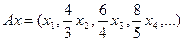 і знайти його норму.
і знайти його норму.
Розв’язування. Для довільних дійсних чисел  і довільних послідовностей
і довільних послідовностей 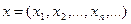 ,
,  є
є  отримаємо:
отримаємо:
 Значить, оператор
Значить, оператор 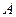 лінійний.
лінійний.
Перевіримо обмеженість оператора. Нехай  – будь-який елемент простору
– будь-який елемент простору  , тоді маємо
, тоді маємо

Тобто  . Значить, оператор
. Значить, оператор 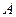 є обмеженим і
є обмеженим і 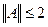 .
.
Припустимо,що існує елемент 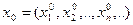 ,
,  ,такий для якого
,такий для якого  . Згідно задання норми в просторі
. Згідно задання норми в просторі  це означає ,що виконується рівність
це означає ,що виконується рівність  . Оскільки для будь-якого
. Оскільки для будь-якого  є
є  справедливі нерівності
справедливі нерівності  і крім того
і крім того  ,то рівність не може виконуватись ні для якого елемента
,то рівність не може виконуватись ні для якого елемента  . Отримали протиріччя.
. Отримали протиріччя.
Розглянемо послідовність елементів  простору
простору  . Норма кожного елемента послідовності дорівнює одиниці. Знайдемо норми елементів
. Норма кожного елемента послідовності дорівнює одиниці. Знайдемо норми елементів 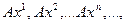 в просторі
в просторі  . Отримаємо:
. Отримаємо:

Звідки випливає, що  тобто норма оператора
тобто норма оператора 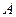 не може бути меншою за число 2.
не може бути меншою за число 2.
Оскільки раніше отримали оцінку 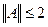 , значить
, значить 
Приклад. Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування. Перевіримо лінійність оператора:  Значить, оператор
Значить, оператор  лінійний.
лінійний.
Для будь-якого елемента  є
є  маємо
маємо
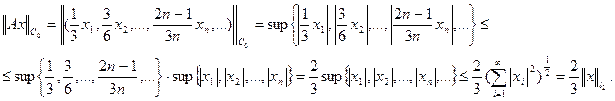
Звідки випливає обмеженість оператора  і оцінка його норми
і оцінка його норми 
Нехай для деякого елемента  є
є  , норма якого рівна одиниці, має місце рівність
, норма якого рівна одиниці, має місце рівність  , тобто
, тобто 
Оскільки  , тому для кожного
, тому для кожного 
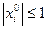 . Дріб
. Дріб  для всіх
для всіх  . Значить, послідовність чисел
. Значить, послідовність чисел  повинна містити підпослідовність
повинна містити підпослідовність 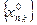 тому, що
тому, що  . Але
. Але  . Отримали протиріччя.
. Отримали протиріччя.
Розглянемо послідовність елементів  з одиничною нормою. Знаходимо
з одиничною нормою. Знаходимо

Звідки отримаємо  , а, значить, норма оператора
, а, значить, норма оператора  не менша за
не менша за 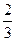 . Отже,
. Отже,  .
.
Приклад. Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування. Перевіримо лінійність оператора. Для довільних дійсних чисел  і довільних елементів
і довільних елементів 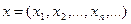 ,
,  є
є  отримаємо:
отримаємо:

Значить, оператор  лінійний.
лінійний.
Візьмемо будь-який елемент  є
є  і оцінимо значення норми елемента
і оцінимо значення норми елемента  в просторі
в просторі  . Маємо
. Маємо

З отриманої оцінки випливає, що оператор  є обмеженим і
є обмеженим і  .
.
Нехай існує елемент  є
є  такий, що
такий, що 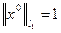 і
і  . Тоді має місце рівність
. Тоді має місце рівність  . Згідно припущення
. Згідно припущення  . Оскільки для кожного
. Оскільки для кожного  дріб
дріб  менший за одиницю, то отримаємо
менший за одиницю, то отримаємо
 , тобто протиріччя.
, тобто протиріччя.
Розглянемо послідовність елементів  простору
простору  з одиничною нормою. Знаходимо
з одиничною нормою. Знаходимо 
Звідки випливає, що  . Значить, норма оператора
. Значить, норма оператора  не може бути меншою за 1. але раніше отримали оцінку
не може бути меншою за 1. але раніше отримали оцінку  . Отже,
. Отже,  .
.
Приклад. Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування. Перевіримо лінійність оператора.
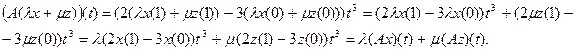
Значить, оператор  є лінійним.
є лінійним.
Для будь-якої функції  отримаємо
отримаємо 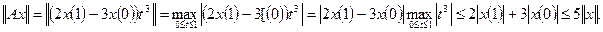
Значить , оператор  обмежений і крім того
обмежений і крім того  .
.
Нехай існує функція  така, що
така, що  і
і  . Тоді справедлива рівність
. Тоді справедлива рівність  . Оскільки найбільше значення функції
. Оскільки найбільше значення функції  на відрізку
на відрізку  дорівнює 1, тому
дорівнює 1, тому  . Звідси випливає, що значення функції
. Звідси випливає, що значення функції  в точках
в точках  повинні бути по модулю рівні 1 і відрізнятися лише знаком.
повинні бути по модулю рівні 1 і відрізнятися лише знаком.
Розглянемо функцію 
 . Вона неперервна на відрізку
. Вона неперервна на відрізку  , і її норма
, і її норма 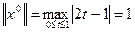 і
і  . Звідси випливає, що
. Звідси випливає, що  .
.
Приклад. Перевірити лінійність, обмеженість оператора 
 і знайти його норму.
і знайти його норму.
Розв’язування. Для довільних дійсних чисел  і довільних неперервних на відрізку
і довільних неперервних на відрізку  функцій
функцій 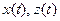 маємо
маємо
 тобто оператор
тобто оператор 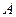 лінійний.
лінійний.
Перевіримо обмеженість оператора. Нехай  - довільна функція з простору
- довільна функція з простору  , тоді отримаємо
, тоді отримаємо  .
.
Звідки випливає, що існує функція  з одиничною нормою , така, для якої
з одиничною нормою , така, для якої  Значить, виконується рівність
Значить, виконується рівність  . Ця рівність справедлива для кожної функції простору
. Ця рівність справедлива для кожної функції простору  , модуль значення якої в точці
, модуль значення якої в точці  дорівнює 1.
дорівнює 1.
Розглянемо функцію  . Ця функція належить простору
. Ця функція належить простору  , норма її рівна 1 і . Отже,
, норма її рівна 1 і . Отже,  .
.
Приклад. Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування.Перевіримо лінійність оператора.

Отже, оператор 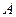 лінійний.
лінійний.
Для довільної функції  простору
простору  маємо
маємо

Таким чином оператор 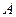 обмежений і
обмежений і 
Покажемо, що норма оператора рівна 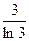 . Розглянемо функцію
. Розглянемо функцію  . Ця функція належить простору
. Ця функція належить простору  і має одиничну норму. Знайдемо норму функції
і має одиничну норму. Знайдемо норму функції  . Отримаємо
. Отримаємо
 .
.
Отже,  .
.
Приклад. Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування. Для довільних дійсних чисел  і довільних функцій
і довільних функцій  маємо:
маємо:
 тобто оператор
тобто оператор 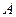 лінійний.
лінійний.
Нехай  – будь-яка функція простору
– будь-яка функція простору  . Оцінимо норму функції
. Оцінимо норму функції  в просторі
в просторі  . Отримаємо:
. Отримаємо:
 Звідки випливає обмеженість оператора і оцінка його норми
Звідки випливає обмеженість оператора і оцінка його норми 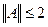 .
.
Припустимо, що існує функція 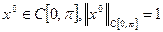 , така, для якої
, така, для якої 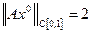 . Тоді виконується рівність
. Тоді виконується рівність 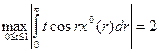 . Оскільки
. Оскільки  , то отримаємо
, то отримаємо  . Функція
. Функція  на відрізку
на відрізку  один раз міняє знак в околі точки
один раз міняє знак в околі точки  з плюса на мінус, крім того
з плюса на мінус, крім того  . А це означає, що рівність
. А це означає, що рівність  може виконуватись тоді і тільки тоді, коли
може виконуватись тоді і тільки тоді, коли  . Функція
. Функція  не належить просторові
не належить просторові  . Значить, отримали протиріччя.
. Значить, отримали протиріччя.
Розглянемо послідовність функцій 
Кожна функція  є неперервною на відрізку
є неперервною на відрізку  , і, як не важко переконатись,
, і, як не важко переконатись, 
Знайдемо норму функції  в просторі
в просторі  . Отримаємо
. Отримаємо

Так як
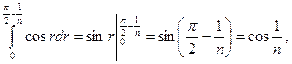

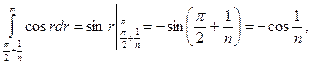 то дістанемо
то дістанемо 
Оскільки  тому
тому  при
при  . Звідси випливає, що
. Звідси випливає, що  . Але раніше отримали оцінку
. Але раніше отримали оцінку 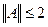 . Отже,
. Отже, 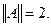
 Приклад.
Приклад.
Перевірити лінійність, обмеженість оператора  і знайти його норму.
і знайти його норму.
Розв’язування. Перевіримо лінійність оператора:
 =
=


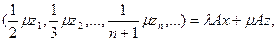 тобто операто
тобто операто 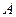 є лінійним.
є лінійним.
Для довільного елемента 
 отримаємо
отримаємо
 =
= 