 |
|
Суммирование случайных погрешностей
Правила суммирования случайных погрешностей основаны на известных из теории вероятностей положениях:
а) оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих;
б) оценка СКО суммарной погрешности определяется выражением
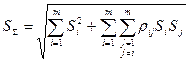(10.7)
где Si – оценка СКО i-й составляющей погрешности; m – число суммируемых составляющих погрешностей; ρij – коэффициент корреляции между i–й и j–й составляющими.
При суммировании m случайных погрешностей их коэффициенты корреляции образуют матрицу, которая ввиду равенства ρij = ρji является диагональной. Так как матрица коэффициентов корреляции симметрична относительно главной диагонали, на которой находятся значения ρii = 1, то формулу (10.7) можно переписать в виде
где суммирование во втором слагаемом распространяется на все те составляющие, коэффициенты, корреляции которых находятся в матрице правее и выше главной диагонали. Их число равно m(m–1)/2.
Использование последнего уравнения и выражения (10.7) затруднительно, так как точное значение коэффициента корреляции между составляющими обычно неизвестно. В этом случае при расчетах полагают ρ=0, если случайные составляющие можно считать независимыми (при 
< 0,7) или ρ = ±1, если заметна корреляция между суммируемыми случайными составляющими погрешностей (при |р| > 0,7).
При необходимости точного учета коэффициента корреляции между погрешностями аргументов Хi и Хj его оценка может быть найдена по формуле
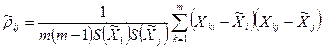(10.8)
где Хki, Хkj – элементы выборки аргументов Хi и Хj; S( 
), S( 
) – оценки СКО средних арифметических результатов измерений аргументов Хi и Хj. Оценку коэффициента корреляции можно определить и по формуле
(10.9)
Полезной может оказаться формула
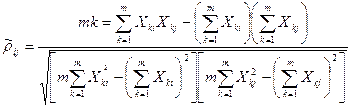(10.10)
основным достоинством, которой является отсутствие необходимости предварительного вычисления СКО составляющих Хki и Хkj. Следует отметить, что формулы (10.8)–(10.10) равнозначны.
В случае суммирования нормально распределенных случайных погрешностей результирующая погрешность измерения состоит из m случайных составляющих. Зная доверительную вероятность Р и доверительный интервал Δ1 для каждой составляющей погрешности, можно найти оценку СКО любой из них по формуле
(10.11)
где zрi – квантиль нормального распределения, соответствующий доверительной вероятности Рi. Если значение Р для всех составляющих одинаково, то, используя выражения (10.7) и (10.11), получаем:
а) для коррелированных составляющих (рij = ± 1)
(10.12)
где знак «±» означает, что для составляющих с положительной корреляцией величины Si и Δi нужно брать со знаком «+», а для составляющих с отрицательной корреляцией – со знаком «–»; б) для независимых составляющих (Pij= 0)
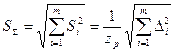(10.13)
При суммировании составляющих с нормальным законом распределения результирующая погрешность также будет распределена нормально. Поэтому доверительный интервал суммарной погрешности с доверительной вероятностью Р может быть найден как
(10.14)
С учетом (10.12) и (10.13) выражение (10.14) принимает вид, соответственно для коррелированных и некоррелированных составляющих:
; 
(10.15)
Суммирование погрешностей по первой формуле называется арифметическим, а по второй – геометрическим. Действительные значения коэффициентов корреляции по абсолютному значению могут находиться в пределах от нуля до единицы, поэтому арифметическое суммирование обычно дает завышенное значение суммарной погрешности, а геометрическое – заниженное, т.е. действительное значение находится в интервале между ними.
Закон распределения результирующей погрешности зависит от конкретных видов и характеристик законов распределения суммируемых составляющих. Исходя из этого для определения доверительного интервала суммарной погрешности необходимо в каждом конкретном случае по известным законам суммируемых составляющих установить методами теории вероятностей результирующий закон распределения. Зная его и соответственно квантильный множитель zр, можно найти доверительный интервал суммарной погрешности по формуле (10.14).