Главная | Обратная связь

Приклади розв’язання задач

Приклад 1. Два точкових заряди 9q і – q закріплені на відстані l=50 см один від одного. Третій заряд q₁ може переміщатися лише вздовж прямої, що проходить через заряди. Визначити положення заряду q_l при якому він буде знаходитися в рівновазі. При якому знаку заряду q₁ рівновага буде стійкою.

Розв’язок. Заряд q₁ перебуває в рівновазі в тому випадку, коли геометрична сума сил, що діють на нього, дорівнює нулю. Це значить, що на заряд q₁ повинні діяти дві сили, рівні за модулем і протилежні за напрямком. Розглянемо, на якій з трьох ділянок І, II, III (рис. 1) може бути виконана ця умова. Для визначеності будемо вважати, що заряд q₁ - позитивний.

На ділянці І (рис.. 1а) на заряд q₁ будуть діяти дві протилежно спрямовані сили: F₁ і F₂. Сила F₁, що діє з боку заряду 9q, у будь-якій точці цієї ділянки більше сили F₂, що діє з боку заряду - q, тому що більший заряд 9q завжди є ближчим до заряду q₁, чим менший (по модулю) заряд - q. Тому рівновага на цій ділянці неможлива.

На ділянці ІІ (рис. 1,б) обидві сили F₁ і F₂ спрямовані в одну сторону - до заряду - q. Отже, і на другій ділянці рівновага неможлива.

На ділянці ІІІ (рис. 1, в) сили F₁ і F₂ спрямовані в протилежні сторони, так само як і на ділянці І, але на відміну від нього менший заряд - q завжди є ближчим до заряду q₁, чим більший заряд 9q. Це значить, що можна знайти таку точку на прямій, де сили F₁ і F₂ будуть однакові за модулем, тобто

(1)

Нехай х і l + х - відстань від меншого і більшого зарядів до заряду q₁. Виражаючи в рівності (1) F₁ і F₂ відповідно до закону Кулона, одержимо

, чи звідки .

Коріньх² не задовольняє фізичній умові задачі (у цій точці сили F₁ і F₂ хоча і рівні за модулем, але мають однаковий напрямок).

Визначимо знак заряду , за якого рівновага буде стійкою. Рівновага називається стійкою, якщо при зсуві заряду від положення рівноваги виникають сили, що повертають його в положення рівноваги. Розглянемо зсув заряду у двох випадках: коли заряд позитивний і негативний.

Якщо заряд позитивний, то при зсуві його вліво обидві сили F₁ і F₂ зростають. Через те, що сила F₁ зростає повільніше, то результуюча сила, що діє на заряд , буде спрямована в ту ж сторону, в яку зміщений цей заряд, тобто вліво. Під дією цієї сили заряд буде віддалятися від положення рівноваги. Те ж відбувається і при зсуві зарядувправо. Сила F₂ убуває швидше, ніж F₁. Геометрична сума сил у цьому випадку спрямована вправо. Заряд під дією цієї сили також буде переміщатися вправо, тобто віддалятися від положення рівноваги. Таким чином, у випадку позитивного заряду рівновага є хиткою.

Якщо заряд негативний, то його зсув уліво викликає збільшення сил F₁ і F₂, але сила F₁ зростає повільніше, ніж F₂, тобто |F₂|;|F₁|. Результуюча сила буде спрямована вправо. Під її дією заряд повертається до положення рівноваги. При зсуві вправо сила F₂ убуває швидше, ніж F₁, тобто |F₁|;|F₂|, результуюча сила спрямована вліво і заряд знову буде повертатися до положення рівноваги. За негативного заряду рівновага є стійкою. Величина самого заряду несуттєва.

Приклад 2. Три точкових заряди Q=Q₂=Q₃=1 нКл розташовані у вершинах рівностороннього трикутника. Який заряд Q₄ потрібно помістити в центрі трикутника, щоб зазначена система зарядів знаходилася в рівновазі?

Розв’язок. Усі три заряди, розташовані по вершинах трикутника, знаходяться в однакових умовах. Тому досить з'ясувати, який заряд варто помістити в центрі трикутника, щоб який-небудь один із трьох зарядів, наприклад Q₁, знаходився в рівновазі. Заряд Q₁ буде знаходитися в рівновазі, якщо векторна сума діючих на нього сил дорівнює нулю (рис.2).

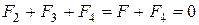, (1)

де F₂, F₃, F₄ - сили, з якими відповідно діють на заряд Q₁ заряди Q₂, Q₃, Q₄; F - рівнодіючих сил F₂ і F₃.

Тому що сили F і F₄ спрямовані по одній прямій у протилежні сторони, та векторна рівність (1) можна замінити скалярним: F – F₄ = 0, звідки F₄=F. Виразивши в останній рівності F через F₂ і F₃ і з огляду на те, що F₃=F₂, одержимо

Застосувавши закон Кулона і маючи на увазі, що Q₂=Q₃=Q₁, знайдемо

звідки

(2)

З геометричних побудов у рівносторонньому трикутнику виходить, що

З урахуванням цього формула (2) набирає вигляду

Зробимо обчислення:

Слід зазначити, що рівновага системи зарядів буде хиткою.

 

Приклад 3. На тонкому стержні довжиноюl=20см знаходиться є розподілений електричний заряд. На продовженні осі стержня на відстані a=10см від найближчого кінця є точковий заряд Q₁=40нКл, що взаємодіє зі стержнем із силою F=6мкН. Визначити лінійну густину tзаряду на стержень.

Розв’язок. Сила взаємодії F зарядженого стержня з точковим зарядом Q₁ залежить від лінійної густини t заряду на стержень. Знаючи цю залежність, можна визначити t. За обчислення сили F варто мати на увазі, що заряд на стержні не є точковим, тому закон Кулона безпосередньо застосувати не можна. У цьому разі можна використати такий спосіб. Виділимо зі стержня (рис. 3) малу ділянку dr із зарядом dQ=tdr. Цей заряд можна розглядати як точковий. Тоді, відповідно до закону Кулона,

Інтегруючи цей вираз у межах від а до a+l, одержуємо

Звідки

 

	Рис.3

 

Перевіримо, чи дає розрахункова формула одиницю лінійної густини електричного заряду. Для цього в праву частину формули замість символів величин підставимо їхні одиниці:

Знайдена одиниця є одиницею лінійної густини заряду.

Зробимо обчислення:

нКл/м

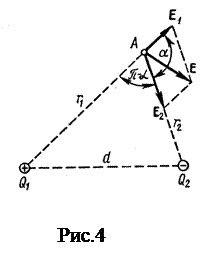
Приклад 4. Два точкових електричних заряди Q₁=1 нКл і Q₂=-2 нКл перебувають у повітрі на відстані d=10см один від одного. Визначити напруженість Е і потенціал j поля, створеного цими зарядами в точці А, яка перебуває від заряду Q₁ на відстані r₁=9 см і від заряду Q₂ на r₂=7 см.

Розв’язок. Відповідно до принципу суперпозиції електричних полів, кожен заряд створює поле незалежне від присутності в просторі інших зарядів. Тому напруженість Е електричного поля в шуканій точці може бути знайдена як геометрична сума напруженостей E₁ і Е₂ полів, утворених кожним зарядом окремо: Е=E₁+Е₂. Напруженості електричного поля, утвореного в повітрі (e=1) зарядами Q₁ і Q₂,

(1)

(2)

Вектор E₁ спрямований по силовій лінії від заряду Q₁, тому що цей заряд позитивний; вектор Е₂ спрямований також по силовій лінії, але до заряду Q₂, тому що цей заряд негативний.

Модуль вектора Е знайдемо за теоремою косинусів:

(3)

де - кут між векторами E₁ і Е₂, що може бути знайдений із трикутника зі сторонами r₁, r₂ і d:

У даному разі, щоб уникнути громіздких записів, зручніше значення cosa обчислити окремо:

Підставляючи вираз Е₁ з (1) і Е₂ з (2) у (3) і виносячи загальний множник 1/(4pe₀) за знак кореня, отримаємо

(4)

Відповідно до принципу суперпозиції електричних полів потенціал j результуючого поля, утвореного двома зарядами Q₁ і Q₂, дорівнює алгебраїчній сумі потенціалів:

(5)

Потенціал електричного поля, утвореного у вакуумі точковим зарядом Q на відстані r від нього, виражається формулою:

(6)

У нашому випадку відповідно до формул (5) і (6) одержимо:

чи

Зробимо обчислення:

Приклад 5.По тонкому кільцю рівномірно розподілений заряд Q=40нКл із лінійною густиною t=50 нКл/м. Визначити напруженість Е електричного поля, утвореного цим зарядом у точці А, що лежить на осі кільця і віддаленої від його центра на відстань, рівну половині радіуса.

Розв’язок. З’єднаємо координатну площину хОуз площиною кільця, а вісь Oz - з віссю кільця (рис. 5). На кільці виділимо малу ділянку довжиною dl. Тому що заряд dQ=tdl, який перебуває на цій ділянці, можна вважати точковим, то напруженість dЕ електричного поля, утвореного цим зарядом, може бути записана у вигляді

де r - радіус-вектор, спрямований від елемента dl до точки А.

Розкладемо вектор dЕ на дві складові: dE₁, перпендикулярно площині кільця (що збігається з віссю Oz), і dЕ₂, паралельну площині кільця (площини хОу) , тобто

Напруженість Е електричного поля в точці А знайдемо інтегруванням:

де інтегрування ведеться по всіх елементах зарядженого кільця. Помітимо, що для кожної пари зарядів dQ і dQ' (dQ=dQ'), розташованих симетрично навколо центра кільця, вектори dЕ₂ і dЕ₂' у точці А рівні за модулем і протилежні за напрямком: dЕ₂=-dЕ₂'.Тому векторна сума (інтеграл) . Складові dЕ₁ для всіх елементів кільця мають спільний напрямок з віссю Oz (одиничним вектором k), тобто dЕ₁= kdЕ_1.

Тоді

Тому, що то

Таким чином:

Зі співвідношення визначимо радіус кільця: .

Тоді

Модуль напруженості:

Перевіримо, чи дає права частина отриманої рівності одиницю напруженості (В/м):

Виразимо фізичні величини, що входять до формули (1), в одиницях СІ

(t= 5^.10^-8 Кл, Q=4^.10^-8 Кл,e₀ =8,85^.10^-12 Ф/м) і зробимо обчислення:

 

Приклад 6. Дві концентричні провідні сфери радіусами R₁=6 см і R₂₌10см несуть відповідно заряди Q₁=1 нКл і Q₂= -0,5 нКл. Знайти напруженість Е поля в точках, що відстоять від центра сфер на відстанях r₁= 5 см ,r₂=9 см, r₃= 15 см. Побудувати графік Е(r).

Розв’язок . Помітимо, що точки, у яких потрібно знайти напруженості електричного поля, лежать у трьох областях (рис. 6) області I(r₁ - R₁), області ІІ (R₁ - r₂ - R₂), області ІІІ (r₃ - R₂).

1. Для визначення напруженості E₁ в області І проведемо гауссовоі поверхні S₁ радіусом r₁ і скористаємося теоремою Остроградського-Гаусса:

,

(тому, що сумарний заряд, який є всередині гауссової поверхні, дорівнює нулю). З розумінь симетрії . маємо,

,

де Е₁ (напруженість поля в області l) у всіх точках, що відповідають умові r₁ - R₁, буде дорівнювати нулю.

2. В області ІІ гауссову поверхню проведемо радіусом r₂. У цьому разі

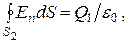
(тому, що усередині гауссової поверхні є лише заряд Q₁).

Тому, що , то можна винести за знак інтеграла:

чи

Позначивши напруженість Е для області ІІ через Е₂, одержимо:

,

де - площа гауссової поверхні. Тоді

(1)

3. В області ІІІгауссова поверхня проводиться радіусом r₃. Позначимо напруженість Е області IIIчерез Е₃ і врахуємо, що в цьому разі гауссова поверхня охоплює обидві сфери і, отже, сумарний заряд буде дорівнювати

Q₁ + Q₂. Тоді

Помітивши, що Q₂ - 0, цей вираз можна переписати у вигляді

(2)

Переконаємося в тому, що права частина рівностей (1) і (2) дає одиницю напруженості:

Виразимо всі величини в одиницях СІ (Q₁=10^-9 Кл, Q₂₌-0,5^.10^-9 Кл, r₁=0,09 м, r₂₌0,15 м, 1/(4pe₀)=9^.10⁹м/ф) і зробимо обчислення:

Побудуємо графік Е(r). В області

I(r₁ - R₁)Е=0, в областіІІ (R₁ - r₂ - R₂)

E₂(r) змінюється за законом 1/ r². У точці r=R₁напруженості

E₂(R₁)=

У точці r=R₂ (r прагне до R₂ ліворуч)

В області ІІІ (r₃ -R₂) Е₃(r) змінюється за законом 1/ r², причому в точці r=R₂(r прагне до R₂ праворуч)

.

Таким чином, функція Е(r) у точках r=R₁ і r=R₂ терпить розрив.

Графік залежності Е(r), подано на рис. 7.

Приклад 7. Точковий заряд Q=25нКл перебуває у полі, створеному прямим нескінченним циліндром радіусом R=1см, рівномірно зарядженим з поверхневою густиною s=0,2 нКл/см². Визначити силу F, що діє на заряд, якщо його відстань від вісі циліндра r =10 см.

Розв’язок. Значення сили F, що діє на точковий заряд Q, що є у полі, визначається за формулою

(1)

де Е - напруженість поля.

Як відомо, напруженість поля нескінченно довгого рівномірно зарядженого циліндра

(2)

де t — лінійна густина заряду.

Виразимо лінійну густину t через поверхневу густину s. Для цього виділимо елемент циліндра довжиною l і виразимо заряд Q, що є на ньому, двома способами: Q=sS=s2pRl, Q=tl.Порівнявши праві частини цих формул і скоротивши отриману рівність на l, знайдемо t=s2pR. З урахуванням цього формула (2) приймає вигляд Підставивши вираз Е у (1), одержимо

Зробимо обчислення:

Сила F збігається за напрямком з напруженістю Е, що через симетрію (циліндр нескінченно довгий) перпендикулярна поверхні циліндра.

Приклад 8. По тонкій нитці, вигнутій по дузі кола, рівномірно розподілений заряд з лінійною густиною t=10 нКл/м. Визначити напруженість Е і потенціал j електричного поля, створеного таким розподіленим зарядом у точці, що збігається з центром кривизни дуги. Довжина l нитки становить 1/3 довжини кола і дорівнює 15 см.

Розв’язок.Виберемо осі координат так, щоб початок координат збігався з центром кривизни дуги, а вісь Оу була б симетрично розташована щодо кінців дуги. На нитці виділимо елемент довжини dl ( рис. 8). Заряд dQ=tdl, що є на виділеній ділянці, можна вважати точковим. Визначимо напруженість електричного поля в точці О. Для цього знайдемо спочатку напруженість dЕ поля, створеного зарядом dQ:

,

де r - радіус-вектор, спрямований від елемента dl до точки, у якій обчислюється напруженість.

Виразимо вектор dЕ через проекції dЕ_х і dЕ_у на осі координат:

де і, j - одиничні вектори напрямків (орти). Напруженість Е знайдемо інтегруванням:

Інтегрування ведеться уздовж дуги довжиною l. Через симетрію . Тоді

(1)

де

Тому, що , тоді:

Підставимо вираз dЕ_у в (1) і, беручи до уваги симетричне розташування дуги щодо осі Оу, межі інтегрування візьмемо від 0 до p/3, а результат подвоїмо:

Виразивши радіус R через довжину l нитки (3l=2pR), одержимо

(2)

З цієї формули видно, що напруженість поля за напрямком збігається з віссю Оу.

Знайдемо потенціал електричного поля в точці О. Спочатку знайдемо потенціал dj, створений точковим зарядом dQ у точці О:

Замінимо r на R і проведемо інтегрування:

Тому, що , то

. (3)

Зробимо обчислення за формулами (2) і (3):

 

Приклад 9. На тонкому стержні довжиною l є рівномірно розподілений заряд з лінійною густиною t=10нКл/м. Знайти потенціал j, утворений розподіленим зарядом у точці А, розташованої на осі стержня і віддаленої від його найближчого кінця на відстань l.

Розв’язок. У задачі розглядається поле, утворене розподіленим зарядом. У цьому разі використовують такий спосіб. На стержні виділяють малу ділянку довжиною dx. Тоді на цій ділянці буде зосереджений заряд dQ=tdх, який можна вважати точковим. Потенціал dj, утворений цим точковим зарядом у точці А (рис. 9) можна визначити за формулою

Відповідно до принципу суперпозиції електричних полів, потенціал електричного поля, утвореного зарядженим стержнем у точці А, знайдемо інтегрування цього виразу:

Виконаємо інтегрування:

Підставимо числові значення фізичних величин у СІ (t =10^.10^-9 Кл/м 1/(4pe₀)=9^. 10⁹м/Ф), і зробимо обчислення:

 

Приклад 10. На пластинах плоского конденсатора є заряд Q=10 нКл. Площа S кожної пластини конденсатора дорівнює 100 см², діелектрик - повітря. Визначити силу F, з якою притягуються пластини. Поле між пластинами вважати однорідним.

Розв’язок.Заряд Q однієї пластини перебуває в полі напруженістю Е, створеному зарядом іншої пластини конденсатора. Отже, на перший заряд діє сила (рис. 10)

(1)

Тому, що

деs - поверхнева густина заряду пластини, то формула (1) прийме вигляд:

Виконаємо обчислення:

Приклад 11.Електричне поле створене довгим циліндром радіусом R=1 см, рівномірно зарядженим з лінійною густиною t=20нКл/м. Визначити різницю потенціалів двох точок цього поля, що перебувають на відстані а₁=0,5 см і а₂=2 см від поверхні циліндра, у середній його частині.

Розв’язок. Для визначення різниці потенціалів скористаємося співвідношенням між напруженістю поля і зміною потенціалу: . Для поля з осьовою симетрією, яким є поле циліндра, це співвідношення можна записати у вигляді

де

Інтегруючи цей вираз, знайдемо різницю потенціалів двох точок, що перебувають на відстанях r₁ і r₂ від вісі циліндра:

(1)

Тому, що циліндр довгий і точки взяті поблизу його середньої частини, то для виразу напруженості поля можна скористатися формулою напруженості поля, створеного нескінченно довгим циліндром:

Підставивши вираз Е в (1), одержимо

чи

Зробимо обчислення, з огляду на те, що величини r₁ і r₂, що входять до формули (2) у вигляді відношення, можна виразити в сантиметрах (r₁=R + а₁=1,5 см, r₂=R + а₂=3 см):

 

Приклад 12. Електричне поле створюється двома зарядами Q₁=4мкКл і Q₂=-2мкКл, що перебувають на відстані а=0,1 м один від одного. Визначити роботу А_1,2 сил поля по переміщенню заряду Q=50 нКл із точки 1 у точку 2 (рис. 11)

Розв’язок. Для визначення роботи А_1,2 сил поля скористаємося співвідношенням

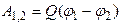
Застосовуючи принцип суперпозиції електричних полів, визначимо потенціали j₁ і j₂ точок l і 2 поля:

Тоді

чи

Перевіримо, чи дає права частина рівності одиницю роботи (Дж):

Підставимо числові значення фізичних величин у СІ (Q=50^.10^-9 Кл, Q₁=4^.10^-6Кл, Q₂=2^.10^-6 Кл, а=0,1 м, 1/(4pe₀) =9^.10⁹ м/Ф) і зробимо обчислення:

 

Приклад 13. Визначити прискорюючу різницю потенціалів U, яку повинен пройти в електричному полі електрон, що має швидкість u= 10⁶ м/с, щоб швидкість його зросла в n=2 рази.

Розв’язок. Різницю потенціалів, що прискорює, можна знайти, обчисливши роботу А сил електростатичного поля. Ця робота визначається добутком елементарного заряду е на різницю потенціалів U:

(1)

Робота сил електростатичного поля в даному разі дорівнює зміні кінетичної енергії електрона:

(2)

де Т₁ і Т₂ - кінетична енергія електрона до і після проходження поля, що прискорює; m - маса електрона; u₁ і u₂ - початкова і кінцева його швидкості.

Порівнявши праві частини рівностей (1) і (2), отримаємо

де n=u₂/u₁.

Звідси шукану різницю потенціалів отримаємо:

Зробимо обчислення:

Приклад 14.З поверхні нескінченного рівномірно зарядженого (t=50 нКл/м) прямого циліндра вилітає

a - частинка (u₀=0). Визначити кінетичну енергію Т₂ a- частинки (кеВ) у точках 1 і 2 на відстані 8R від поверхні циліндра (рис. 12).

Розв’язок.Тому, що сили електростатичного поля є консервативними то, для визначення кінетичної енергії a- частинки в точці 2 скористаємося законом збереження енергії, записаному у вигляді Е₁=Е₂, де Е₁ і Е₂ - сповненої енергії a-частинки в точках l і 2.

Так як E₁=T₁+U₁ і E₂=T₂+U₂ (Т₁ і Т₂ - кінетичні енергії a -частинки; U₁ і U₂ — потенційні), тоді, з огляду на те, що Т₁=0 (u₀=0), можна записати U₁=T₂+U₂, звідки (Q - заряд a- частинки; j₁ і j₂ - потенціали точок 1 і 2).

Використовуючи рішення прикладу 11, запишемо:

Виразимо всі величини в одиницях СІ

(Q=2^.1,60^.10^-19 Кл, t=50^.10^-9 Кл/м, 1/(2pe₀)= 18^.10⁹ м/Ф) і зробимо обчислення

(1/(1,60^.10^-19) — коефіцієнт перекладу з Дж в еВ):

 

Приклад 15. Конденсатор ємністю С₁=3 мкФ був заряджений до різниці потенціалів U₁=40B. Після відключення від джерела струму конденсатор з'єднали паралельно з іншим незарядженим конденсатором ємністю С₂=5 мкФ. Яка енергія W витратиться на утворення іскри в момент приєднання другого конденсатора?

Розв’язок. Енергія, витрачена на утворення іскри

(1)

де W₁ - енергія, яку мав перший конденсатор до приєднання до нього другого конденсатора; W₂ - енергія, що має батарея, складена з двох конденсаторів.

Енергія зарядженого конденсатора визначається за формулою

(2)

де С - ємність конденсатора чи батареї конденсаторів.

Виразивши з формули (1) енергії W₁ і W₂ за формулою (2) і беручи до уваги, що загальна ємність паралельно з'єднаних конденсаторів дорівнює сумі ємностей окремих конденсаторів, одержимо

(3)

де U₂ - різниця потенціалів на затисках батареї конденсаторів.

З урахуванням того, що заряд після приєднання другого конденсатора залишився таким же, виразимо різницю потенціалів U₂ у такий спосіб:

(4)

Підставивши вирази U₂ у (3), знайдемо

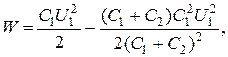чи

Зробимо обчислення:

 

Приклад 16. Потенціометр опором R=100Ом підключений до батареї з ЕРСe=150В і внутрішнім опором R_i=50Ом. Визначити:

1) показання вольтметра опором R_V=500Ом, з'єднаного з однією з клем потенціометра і рухливим контактом, установленим посередині потенціометра;

2) різницю потенціалів між тими ж точками потенціометра при відключенні вольтметра.

Розв’язок. 1. Показання вольтметра, підключеного до точок А і В

(рис. 13), визначимо за формулою

,

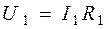де R₁ - опір паралельно з'єднаних вольтметра і половини потенціометра; І₁ - сумарна сила струму в галузях цього з'єднання (вона дорівнює силі струму в нерозгалуженій частині ланцюга).

Силу струму І₁ знайдемо за законом Ома для повного ланцюга:

, (1)

де R_e - опір зовнішнього ланцюга. Цей опір є сума двох опорів:

. (2)

Опір R₁ знайдемо по формулі паралельного з'єднання провідників , звідти .

Підставивши в (1) вираз R_e по (2), знайдемо

.

У даному разі розв’язок задачі в загальному вигляді було б громіздким. Тому зручно обчислення величин зробити окремо:

2. Різниця потенціалів між точками А і В при відключеному вольтметрі дорівнює добутку сили струму І₂ на половину опору потенціометра:

(3)

де І₂ — сила струму в ланцюзі при відключеному вольтметрі. Її визначимо за формулою

.

Підставивши вираз І₂у (3), знайдемо

Зробимо обчислення:

 

Приклад 17. Сила струму в провіднику опором R=20 Ом зростає протягом часу Dt=2с за лінійним законом від I₀=0A до I₁₌6А (рис.14). Визначити теплоту Q₁, що виділилася в цьому провіднику за першу секунду, і Q₂ - за другу, а також знайти відношення Q₂/Q₁.

Розв’язок. Закон Джоуля-Ленца у вигляді Q=I²Rt справедливий для постійного струму (І=const). Якщо ж сила струму в провіднику змінюється, то закон зазначений нескінченно малий інтервал часу записується у вигляді

, (1)

де сила струму Іє деякою функцією часу. У даному разі

(2)

де k - коефіцієнт пропорційності, що характеризує швидкість зміни сили струму:

З урахуванням (2) формула (1) матиме вигляд

. (3)

Для визначення теплоти, що виділилася за кінцевий інтервал часу Dt, вираз (3) треба проінтегрувати в межах від t₁ до t₂.

Зробимо обчислення:

відповідно за другу секунду виділиться теплоти в сім разів більше, ніж за першу.