Главная | Обратная связь

Множення двох виміряних значень

Мабуть, найбільш важлива особливість в понятті відносної погрішності проявляється при множенні виміряних значень один на одного. Наприклад, щоб знайти імпульс тіла, ми могли б виміряти його масу т і швидкість v, потім перемножити їх і отримати імпульс p=mv. обидві величини m i v мають похибки, які ми повинні оцінити. Потім виникає завданняі знайти похибку у р, яка є слідством відомих похибок m i v.

Для зручності запишемо число у стандартному вигляді

 

(виміряне значення х) = х_найк ± Δх

 

і, використовуючи поняття відносної похибки,

 

(виміряне значення х) = х_найк 2.22

Наприклад, якщо відносна похибка становить 3 %, то за 2.22 маємо:

 

(виміряне значення х) = х_найк ,

тобто похибка у 3 % значить, що х імовірно лежить між значеннями х_найк ∙ 0,97, і х_найк ∙ 1,03.

 

(0,97) ∙ х_найк ≤ х ≤ (1,03) ∙ х_найк

 

Ми побачимо, що це корисна форма представлення числа, яке хочемо помножити.

Повернемось тепер до нашої задачі обчислення p=mv , коли m i v були вимиіряні як

 

(виміряне значення m) = m_найк 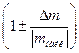(2.23)

і

(виміряне значення v) = v_найк (2.24)

 

Оскільки m_найк і v_найк є найкращі оцінки для m i v, то найкраща оцінка для р= mv, є

р_найк = m_найк ∙ v_найк

Найбільше імовірне значення для m i v дають вирази (2.23) і (2.24) зі знаком плюс.

Таким чином, найбільше імовірне значення для р= mv є

(найбільше імовірне значення р) = m_найк ∙ v_найк (2.25)

 

Найменше імовірне значення для р дають аналогічні вирази зі знаком мінус. тепер результат добутку дужок у (2.25) може бути представлений у вигляді

 

= 1+ + + ∙ (2.26)

 

Оскільки дві відносні похибки і – малі числа ( можливо, порядка декількох відсотків), то їх добуток дуже малий і останнім членом виразу (2.26) можна знехтувати. Повертаючись до (2.25), ми отримуємо

(найбільше імовірне значення р) = m_найк ∙ v_найк

 

Найменше імовірне значення дається аналогічним виразом з двома знаками мінус.

Наші виміри m i v приводять до значення р= mv , що визначається виразом

 

(значення р ) = m_найк ∙ v_найк

Порівнюючи цей вираз із загальною формою запису

(значення р ) = р_найк

 

ми бачимо, що найкраща оцінка для р є р_найк = m_найк ∙ v_найк і відносна похибка р дорінює сумі відносних похибок m i v.

 

= +

 

Якщо, наприклад, у нас були наступні значення для m i v:

 

m = 0,53 ± 0,01 кг

v = 9,1 ± 0,3 м/с,

 

то найкраща оцінка для р= mv дорівнює:

 

р_найк = m_найк ∙ v_найк =(0,53) ∙ (9,1) = 4,82 кг∙м/с

 

Для розрахунку похибки у р обчислимо спочатку відносні похибки

 

=

і

=

Відносна похибка в р є сума

= 2 % + 3 % = 5 %

 

Якщо ми захочемо визначити абсолютну похибку в р, необхідно помножити отримане число на р_найк.

 

Потім, зокруглюючи, одержимо залишкову відповідь:

 

(значення р) = 4,8 ± 0,2 кг∙м/с

 

Попередній розгляд може бути застосовано до будь-якого добутку двох виміряних величин. Таким чином, ми отримали друге загальне правило для непрямих вимірів. Якщо ми вимірюємо дві величини і шукаємо їх добуток, то похибки в початкових двох величинах "поширюються" і утворюють похибку у їх добутку. Ця похибка дається наступним правилом:

 

Похибка в добутку

Якщо величини х і у виміряні з малими

відносними похибками і і,

якщо виміряні величини х і у використовуються

для обчислення добутку q=xy, то відносна похибка

q дорівнює сумі віднорсних похибок х і у:

(2.2)

 

 

Ми використовували знак наближеної рівності в (2.27), оскільки, як і у разі правила обчислення погрішності для різниці, ми пізніше замінимо (2.27) точнішим правилом. Слід підкреслити також дві інші особливості, цього правила. По-перше, при виведенні виразу (2.27) передбачалося, що відносні похибки і у мають бути досить малі, щоб їх добутком можна було знехтувати. На практиці це умова майже завжди виконується, так що ми його завжди припускатимемо. Проте слід пам'ятати, що якщо відносні похибки ненабагато менше одиниці, то правило 2.27) непридатно.

По-друге, навіть якщо х і у мають різну розмірність те в рівняння (2.27) входять безрозмірні величини, оскільки усі відносні похибки безрозмірні. У фізиці ми постійно перемножуємо числа, тому очевидно, що правило (2.27) для знаходження похибки в добутку відіграє важливу роль в теорії похибок. В даний момент наша головна мета - підкреслити, що похибка будь-якого добутку q = ху найпростіше визначається через відносні похиибки виразом типу (2.27).

 

Глава 3