Главная | Обратная связь

I. Статистическое оценивание

Статистическое оценивание – это анализ выборочных характеристик. Его преимуществами являются:

• результаты выборочного исследования объективны и обоснованны, поскольку определение объема выборки основано на точно сформулированных статистических принципах;

• метод выборочного исследования позволяет заранее определить объем выборки;

• метод позволяет оценить ошибку выборочного исследования;

• этот подход можно применять для более точной оценки параметров, поскольку исследование большой генеральной совокупности может занять много времени и даже сопровождаться значительными ошибками нестатистического характера;

• Метод выборочного исследования позволяет объективно оценить результаты проверки, поскольку его точность известна заранее.

Случайная выборка из n элементов — это такой отбор, при котором элементы извлекаются по одно­му из всей генеральной совокупности и каждый из них имеет равный шанс быть отобранным. Требо­вание случайности обеспечивается отбором по таб­лицам случайных чисел или по жребию. Такая выборка называется собственно-случайной. Одним из примеров использования собственно-случайной выборки является проведение тиражей выигрышей денежно-вещевых лотерей, при которых обеспечи­вается равная возможность попадания в тираж лю­бого номера лотерейного билета.

По способу отбора элементов различают два типа случайных выборок: собственно-случайная повтор­ная (схема возвращенного шара); собственно-случай­ная бесповторная (схема невозвращенного шара).

Выбор схемы отбора зависит от характера изучае­мого объекта. При повторном отборе единица наблюдения после извлечения из генераль­ной совокупности регистрируется и вновь возвраща­ется в генеральную совокупность, откуда опять мо­жет быть извлечена случайным образом. При бес­повторном отборе элемент в выборку не возвращает­ся. Следует отметить, что независимо от способа орга­низации выборки она должна представлять собой уменьшенную копию генеральной совокупности, т.е. быть представительной (репрезентативной).

Числовые характеристики генеральной совокуп­ности, как правило, неизвестны (математическое ожидание, диспер­сия и др.), называются параметрами генеральной совокупности. Их обозначают:μ, 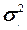. Доля единиц, обладающих тем или иным при­знаком в генеральной совокупности, называется ге­неральной долейи обозначается буквой р.

По данным выборки рассчитывают числовые характеристики, которые называют статистиками. Обозначим выборочные статистики для среднего арифметического, дисперсии и доли соответственно через 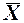, 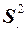и р_n.Одноименные статистики, получаемые по раз­личным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из вы­борки, является только оценкойнеизвестного пара­метра генеральной совокупности. Оценка парамет­ра — это определенная числовая характеристика, по­лученная из выборки.Желательно, чтобы оценки параметров генеральной совокупности обладали свойствами несмещенности, состоятельности и эффективности.

Несмещенная оценка означает свойство, состоящее в том, что математическое ожидание оценки (например, средняя выборочного распределения) равно параметру генеральной совокупности (М(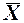 )=μ). При соблюдении этого свойства в результате осуществления множества выборок для определения оценки одни выборочные показатели будут больше параметра генеральной совокупности, другие меньше, но среднее значение будет равно параметру генеральной совокупности. Напротив, при смещенной оценке среднее значение будет больше или меньше параметра генеральной совокупности.

Состоятельность – это свойство оценки, согласно которому дисперсия оценки уменьшается до нуля с увеличением объема выборки до бесконечности.

Оценки, которые одновременно и несмещенные, и имеют наименьшую дисперсию, называются эффективными оценками.

Когда оценка определяется одним числом, ее называют точечной оценкой.

В качестве точечных оценок параметров генераль­ной совокупности используются соответствующие выборочные характеристики. Теоретическое обосно­вание возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чи­сел. Смысл его результатов заключается в том, что при осреднении большого числа (n) случайных слагаемых все менее ощуща­ется характерный для случайных величин неконтролируемый разброс в их значениях, так что в пределепри этот разброс исчезает вовсе или, как принято говорить, случайная величина вырождается в неслучай­ную. Однако при любом конечном числе слагаемых пслучайный разброс у среднего арифметического этих слагаемых остается. Поэтому возникает вопрос исследования характера этого разброса.

Выборочная средняя является точечной оценкой генеральной средней, т.е.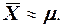

Генеральная дисперсия имеет 2 точечные оцен­ки: σ²_выб. — выборочная дисперсия; S²— исправлен­ная выборочная дисперсия[4]. σ²_выб исчисляется при п > 30, a S² — при п < 30. Причем в математичес­кой статистике доказывается, что

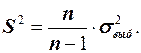
При больших объемах выборки σ²_выб и S² практи­чески совпадают.

Поскольку выборочная совокупность представля­ет собой лишь часть генеральной совокупности, то вполне естественно, что выборочные характеристи­ки не будут точно совпадать с соответствующими генеральными. Ошибка репрезентативности может быть представлена как разность между генераль­ными и выборочными характеристиками изучаемой совокупности: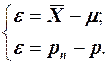

Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала и оценивается по формуле:

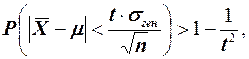(1)

 

где 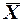— среднее арифметическое по совокупности выбранных еди­ниц;

μ — среднее арифметическое по генеральной совокупности;

σ_ген — среднее квадратическое отклонение в гене­ральной совокупности;

t – коэффициент доверия.

В дальнейшем нижний индекс при обозначении среднего квадратического отклонения в гене­ральной совокупности будем опускать, а среднее квадратическое отклонение по выборке обозначать через S.

Согласно центральной предельной теореме, выборочные распределения статистик (при п > 30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная со­вокупность. Следовательно,

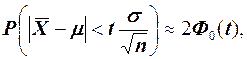(2)

где Ф₀(t) — функция Лапласа. Эта функция часто используемся для вычисления вероятности попадания случайной величины Х, распределеннойпо нормальному закону 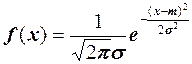в интервал от значения α до значения β:

.

 

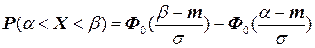Выражение (2) показывает, что о величине расхождения между 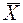и μ можно судить лишь с определенной вероятностью, значение которой зависит от стандартной ошибки (standard error) выборочных средних 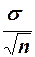и показателя t. Поэтому в теории статистического анализа для оценки характеристик генеральной совокупности помимо точечных оценок используются и интервальные оценки.

При выборочном исследовании генеральной совокупности и формулировании статистических выводов часто возникают этические проблемы. Основная из них — как согласуются доверительные интервалы и точечные оценки выборочных статистик. Публикация точечных оценок без указания соответствующих доверительных интервалов (как правило, имеющих 95%-ный доверительный уровень) и объема выборки, на основе которых они получены, может породить недоразумения. Это может создать у пользователя впечатление, что точечная оценка — именно то, что ему необходимо, чтобы предсказать свойства всей генеральной совокупности. Таким образом, необходимо понимать, что в любых исследованиях во главу угла должны быть поставлены не точечные, а интервальные оценки. Кроме того, особое внимание следует уделять правильному выбору объемов выборки. Чаще всего объектами статистических манипуляций становятся результаты социологических опросов населения по тем или иным политическим проблемам. Чтобы доказать обоснованность полученных точечных оценок, необходимо указывать объем выборки, на основе которой они получены, границы доверительного интервала и его уровень значимости.

Интервальной оценкой называют оценку, кото­рая определяется 2 числами — концами интерва­ла, который с определенной вероятностью накры­вает неизвестный параметр генеральной совокуп­ности. Интервал, содержащий оцениваемый пара­метр генеральной совокупности, называют дове­рительным интервалом.

Для его определения вы­числяется предельная ошибка выборки, позволя­ющая установить предельные границы, в которых с заданной вероятностью (надежностью) должен на­ходиться параметр генеральной совокупности.

Предельная ошибка выборки равна t - кратному числу средних ошибок выборки. Коэффициент tпозволяет установить, насколько надежно выска­зывание о том, что заданный интервал содержит параметр генеральной совокупности. Если мы вы­берем коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% — неправильным, то мы говорим: со статистичес­кой надежностью в 95% доверительный интервал выборочной статистики содержит параметр гене­ральной совокупности.Статистической надежности в 95% соответствует доверительная вероятность — 0,95. В 5% случаев утверждение «параметр принадлежит доверительному интервалу» будет неверным, т. е. 5% задает уровень значимости(α),или вероятность ошибки равна 0,05. Обычно в статистике уровень значимости выбирают таким, чтобы он не превы­сил 5% (α < 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания (см. рис.1).

 

Доверительный уровень равный 95%, интерпретируется следующим образом:

если из генеральной совокупности извлечь все выборки, имеющие объем п, и вычислить их выборочные средние, то 95% доверительных интервалов, построенных на их основе, будут содержать математическое ожидание генеральной совокупности, а 5% — нет.

 

 

Рис. 1. Доверительный интервал и предельная ошибка выборки