 |
|
Способи задання площини
РОЗДІЛ 1. Теоретичні відомості до модуля «Площина в просторі»
Поняття площини та її рівняння
В курсі елементарної геометрії площина не визначається, так як вона є основним, неозначуваним геометричним об’єктом. Основні властивості площини задаються аксіомами, а інші виводяться з них логічним шляхом. Однак, користуючись поняттям компланарності векторів, можна задати геометричне місце всіх точок простору, що належать площині. Дійсно, якщо М0 — довільна точка площини  , а
, а 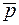 і
і  — неколінеарні вектори, паралельні цій площині, то точка М належить площині
— неколінеарні вектори, паралельні цій площині, то точка М належить площині  тоді і тільки тоді, коли вектори
тоді і тільки тоді, коли вектори 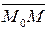 ,
, 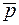 і
і  компланарні. Іншими словами, якщо
компланарні. Іншими словами, якщо  — множина всіх точок, що належать площині
— множина всіх точок, що належать площині  , то
, то  –– геометричне місце точок М простору, що задовольняють умові: вектори
–– геометричне місце точок М простору, що задовольняють умові: вектори  ,
, 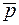 і
і  компланарні. Ця властивість може бути використана для складання рівняння геометричного місця точок
компланарні. Ця властивість може бути використана для складання рівняння геометричного місця точок  , тобто рівняння площини.
, тобто рівняння площини.
Способи задання площини
- Площина задається точкою і направляючим підпростором
Вектори, які лежать в одній площині, називаються направляючим двовимірним векторним підпростором трьохвимірного векторного простору.
 Нехай
Нехай  – довільна площина,
– довільна площина,  – точка, що належить площині
– точка, що належить площині  , а вектори
, а вектори  і
і  визначаютьнаправляючий підпростір даної площини (рис. 1). Візьмемо в площині
визначаютьнаправляючий підпростір даної площини (рис. 1). Візьмемо в площині  довільну точку
довільну точку  . Оскільки вектори
. Оскільки вектори  ,
, 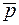 і
і  компланарні, то виконується умова:
компланарні, то виконується умова:
 (1)
(1)
Рівняння (1) є рівнянням площини, що задається точкою і направляючим підпростором.
2. Рівняння площини, що проходить через три точки, які не лежать на одній прямій
Нехай маємо три точки  ,
, 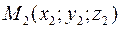 ,
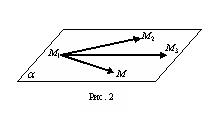
,  , які не лежать на одній прямій (рис. 2).
, які не лежать на одній прямій (рис. 2).
Розглянемо вектори 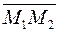 ,
,  . Ці вектори не колінеарні, а тому довільна точка
. Ці вектори не колінеарні, а тому довільна точка  лежить на одній площині з точками
лежить на одній площині з точками 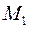 ,
,  ,
, 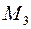 тоді й тільки тоді, коли вектори
тоді й тільки тоді, коли вектори 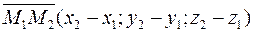 ;
;  ;
; 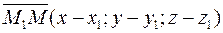 будуть компланарними. Якщо вектори компланарні, то їх мішаний добуток дорівнює нулю:
будуть компланарними. Якщо вектори компланарні, то їх мішаний добуток дорівнює нулю:

Запишемо цю умову у вигляді:
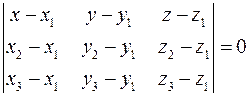 (2)
(2)
Рівняння (2) називається рівнянням площини, що проходить через три дані точки.
3. Рівняння площини у відрізках
Нехай площина  відтинає на осях координат відрізки
відтинає на осях координат відрізки  Тоді
Тоді  ,
,  ,
,  – точки перетину площини
– точки перетину площини  з осями координат (рис. 3). Якщо
з осями координат (рис. 3). Якщо  – довільна точка даної площини, то виконується умова компланарності векторів
– довільна точка даної площини, то виконується умова компланарності векторів  ,
,  ,
,  :
:


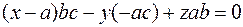

 (3)
(3)
Рівняння (3) називається рівнянням площини у відрізках.
4. Параметричні рівняння площини
Нехай площина  задана точкою
задана точкою  і направляючими векторами
і направляючими векторами  та
та  . Оскільки вектори
. Оскільки вектори 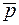 і
і  не колінеарні, то вектор
не колінеарні, то вектор  єдиним чином можна розкласти по векторах
єдиним чином можна розкласти по векторах 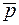 і
і  , тобто для будь-якої точки
, тобто для будь-якої точки  площини
площини  існують числа
існують числа  та
та  такі, що
такі, що
 (4)
(4)
Запишемо рівність (4) в координатній формі:
 або
або  (5)
(5)
Рівняння (5) називаються параметричними рівняннями площини.
5. Загальне рівняння площини
 Нехай площина
Нехай площина  проходить через точку
проходить через точку  перпендикулярно до вектора
перпендикулярно до вектора  (рис. 4).
(рис. 4).
Цими умовами визначається єдина площина у просторі. Вектор 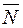 називається нормальним вектором площини
називається нормальним вектором площини  . Візьмемо в площині
. Візьмемо в площині  довільну точку
довільну точку  . Тоді вектор
. Тоді вектор  буде перпендикулярним до вектора
буде перпендикулярним до вектора  . Значить, скалярний добуток цих векторів дорівнює нулю, тобто
. Значить, скалярний добуток цих векторів дорівнює нулю, тобто 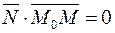 .
.
Одержане рівняння запишемо в координатній формі:


Рівняння площини, записане у вигляді
 (6)
(6)
(де 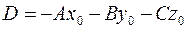 ), називається загальним рівнянням площини.
), називається загальним рівнянням площини.