 |
|
Способы вычисления поверхностных интегралов
В общем случае от поверхностного интеграла второго рода можно перейти к поверхностному интегралу первого рода по следующей формуле: 
, где 
– сторона поверхности 
, которая обращена в сторону положительного направления оси 
.
– вектор нормали к поверхности , который состоит из направляющих косинусов. Если поверхность задана уравнением 
, то направляющие косинусы могут быть вычислены по формулам: 
; 
; 
, где 
. Знак «+» перед радикалом ставим в случае взятия интеграла по поверхности .
Другой способ вычисления поверхностных интегралов второго рода заключается в проектировании на координатные плоскости. Так если поверхность имеет проекции 
, 
, 
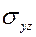на координатные плоскости 
, 
, 
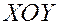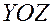соответственно, а уравнение поверхности выражается как 
, 
, 
, то справедлива формула перехода от поверхностного интеграла второго рода к сумме трёх двойных:
.
Если – замкнутая поверхность, то интеграл по внешней её стороне обозначается через 
, а по внутренней: 
.
Пример
Вычислить поверхностный интеграл второго рода. 
, где задаётся неравенством: 
.
Проекция на координатную плоскость 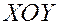представляет собой круг 
. Перейдём к двойному интегралу для вычисления которого лучше перейти к полярным координатам: 
, 
, 
. Так как мы интегрируем по части цилиндра, расположенной ниже координатной плоскости 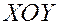, то перед двойным интегралом поставим знак минус. Получаем:
.
Ответ: 
.
Вычислить поверхностный интеграл второго рода. 
, где – внешняя сторона эллипсоида, расположенная в первом октанте. задаётся уравнением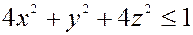 
.
Данный эллипсоид проектируется на координатные плоскости следующим образом: на координатную плоскость 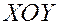: – это часть эллипса 
, расположенная в первой координатной четверти, на координатную плоскость : – это часть круга 
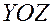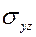, расположенная в первой координатной четверти, на координатную плоскость : – это часть эллипса 
, расположенная в первой координатной четверти.
где: 
– численно равен площади эллипса с полуосями 
, 
, т.е. 
.
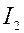лучше всего вычислить, перейдя к полярным координатам: , , . Следовательно, получаем: 
.
.
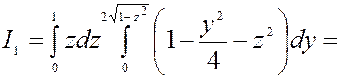
Отсюда: 
.
Ответ: 
.
Вычислить поверхностный интеграл второго рода. 
, где – внешняя сторона поверхности тетраэдра 
, ограниченного плоскостями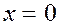 
, 
, 
, 
.
Поверхность имеет вид: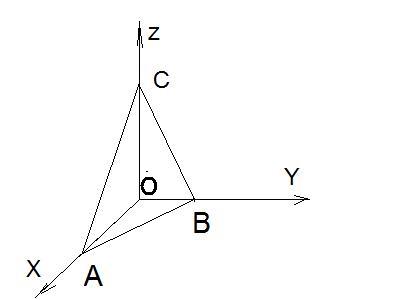 
Проекция на координатную плоскость есть 
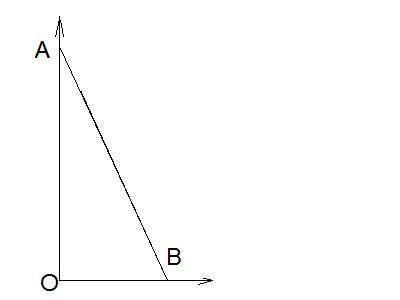
В данном случае 
. Отсюда, 
. 
. Получаем:
.
Здесь был вычислен интеграл только по одной грани: 
. По трём остальным граням вычислять не нужно, так как их проекции на координатные плоскости – отрезки, а, значит, интеграл по ним равен нулю.
Ответ: 
.