Главная | Обратная связь

Поверхности второго порядка

 

Общий вид уравнения поверхности в пространстве:

F(x,y,z)=0 или z=f(x,y)

(в декартовой системе координат).

Поверхностями второго порядка называются такие поверхности, уравнения которых в декартовой системе координат являются уравнениями второй степени относительно x,y,z, т.е. имеют вид:

Ax²+2By²+Cz²+Dxy+Exz+Fyz+Gx+Hy+Kz+L=0.

Примером поверхностей второго порядка является сфера:

(x--x₀)²+(y --y₀)²+(z --z₀)²=R² или

x²+y²+z²--2x₀x--2y₀y--2z₀z+(x₀²+ y₀²+ z₀²-R²)=0.

I. Эллипсоид.

Эллипсоидом называется поверхность, уравнение которой в декартовой системе координат имеет вид (рис.30):

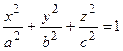
Рис. 30.

Исследуем форму этой поверхности методом сечений.

1. х =0 (плоскость Оуz): (эллипс)

2. у =0 (плоскость Охz): 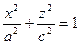(эллипс)

3. z=0 (плоскость Оxy): 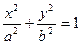(эллипс)

Плоскость z=h (параллельна плоскости Оxy ) . Если , то точек пересечения поверхности и плоскости нет. Если , то в сечениях получаются эллипсы:

Если h=0, то полуоси эллипса и имеют наибольшее значение a и b.

Если a=b, то эллипсоид получен вращением эллипса 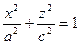вокруг оси Оz.

Если a=b=c, то получаем сферу.

z

II. Однополостный гиперболоид.

0

y

x

Однополосным гиперболоидом называется поверхность, уравнение которой в декартовой системе координат имеет вид (рис.31):

Рис. 31.

Исследуем форму поверхности методом сечений.

1. х =0 (плоскость Оуz): - гипербола с действительной осью Оу

2. у =0 (плоскость Охz): - гипербола с действительной осью Ох.

3. z =0 (плоскость Оxy): 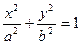- эллипс.

z=h (плоскость, параллельная плоскости Оxy ):

или - эллипсы. При увеличении полуоси эллипсов возрастают.

Если a=b, то поверхность называется однополосным гиперболоидом вращения. Её можно получить вращая гиперболу вокруг оси Oz.

III. Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид (рис. 32):

 

.

 

Рис. 32.

Исследуем форму поверхности методом сечений:

1. х=0 (плоскость Оyz): - гипербола с действительной осью Oz.

2. у=0 (плоскость Оxz): - гипербола с действительной осью Oz.

3.z=h (плоскость, параллельная плоскости Оху): .

Если , то поверхность не пересекается с плоскостью.

Если , то - эллипсы.

При увеличении полуоси эллипсов возрастают.

Если a=b, то получаем двуполостный гиперболоид вращения:

.

Его можно получить, вращая гиперболу вокруг оси Oz.

IV. Эллиптический параболоид.

Эллиптическим параболоидом называется поверхность, определяемая в декартовых координатах уравнением (рис. 33):

(p>0, q>0)

 

Исследуем форму методом сечений: Рис. 33.

1. х=0 (плоскость Оyz): или - парабола с осью Oz.

2. y=0 (плоскость Оxz): или - парабола с осью Oz.

3. z=h (плоскость, параллельная плоскости Оху): .

Если h<0, то точек пересечения нет.

Если h>0, то - эллипс.

Если p=q, то поверхность называется параболоидом вращения. Её можно получить, вращая параболу 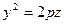вокруг оси Oz.

V. Гиперболический параболоид.

Гиперболический параболоидом называется поверхность, определяемая в декартовой системе координат уравнением:

 

 

Рис.34.

(p>0, q>0).

Исследуем форму методом сечений:

1. у=0 (плоскость Оxz): или парабола АОА₁.

2. х=0 (плоскость Оyz): или (парабола ВОВ₁, z<0).

3. z=h (плоскость параллельная плоскости Оху) .

Если h>0, то получаем гиперболы с вещественной осью, параллельной Ох (D₁D₂ и D₃D₄).

Если h<0, то ось гипербол параллельна оси Оу.

VI. Конус второго порядка.

Конусом второго порядка называется поверхность, уравнение которой в декартовой системе координат имеет вид (рис. 35):

.

 

Рис. 35.

Исследуем форму методом сечений:

1. х=0 (плоскость Оуz): - пара прямых, проходящих через начало.

2. y=0 (плоскость Охz): 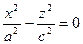- пара прямых, проходящих через начало координат.

3. z=h (плоскость параллельная плоскости Оху) 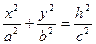(эллипсы).

6.Цилиндрические поверхности.

 

Поверхность называется цилиндрической, если она может быть образована перемещением прямой параллельно самой себе вдоль некоторой линии L.

 

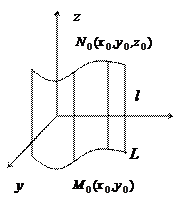l-образующая цилиндрической поверхности, а L – на-

правляющая.

 

.

x

Пусть кривая L в плоскости Оху задана уравнением:

F(x,y)=0. (19)

 

Рис. 36.

Покажем, что уравнение (19) в пространстве Oxyz определяет цилиндрическую поверхность с образующей параллельной оси Oz и направляющей L. Рассмотрим соответствующую цилиндрическую поверхность S.

Возьмём на кривой L произвольную точку M₀(x₀,y₀) и восстановим из неё перпендикуляр к плоскости Оху, и на нём возьмём точку N₀(x₀,y₀,z₀).

Пусть , тогда и её координаты удовлетворяют уравнению (19):

F(x₀,y₀)=0.

Так как (19) не содержит z, то ему удовлетворяют и координаты точки N₀. Координаты точек не удовлетворяют уравнению (19), так как эти точки проектируются на плоскость Оху вне кривой L.

Рассмотрим цилиндры второго порядка, т.е. цилиндры, направляющими L которых служат кривые второго порядка

А). Эллиптический цилиндр:

Рис. 37.

Если a=b=R, то имеем круговой цилиндр:

Б). Гиперболический цилиндр .

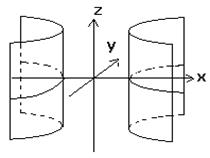
Рис. 38.

В сечении плоскостью z=h – гиперболы.

 

 

В). Параболический цилиндр: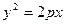

Рис. 39.

В сечении плоскостью z=h – параболы.