Косвенные измерения

Обычно приходится вычислять искомую величину по результатам измерений других величин, связанных с этой величиной определенной функциональной зависимостью. Такие измерения называются косвенными. Например, плотность тела (пластины) ρ определяется через массу тела и его объем:

где L, b, h - линейные размеры пластины.

Величины m, L, b, h можно измерить, а затем вычислить плотность ρ.

Итак, чаще всего искомая величина является функцией нескольких переменных:

A = f(x, y, z, …) (0.15)

Если величины х, у, z,... случайны, то А тоже будет случайной величиной.

Из теории вероятностей известно, что среднее значение функции случайной величины приближенно равно функции от средних значений ее аргументов при условии, что погрешности измерений аргументов ∆х, ∆y, ∆z,... малы по сравнению с величинами х, у, z,..., то есть

, (0,16)

где - среднее значение величины А, - средние значения величин x, y, z, …(см.формулу 0.1).

Для оценки доверительной границы случайной погрешности косвенного измерения применяют формулу:

(0.17)

где ∆x_гр, ∆y_гр, ∆z_гр, … доверительные границы случайных погрешностей величин х, у, z,... при одинаковой w; , , 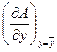, … - частные производные функции А по х, у, z,..., вычисленные при , , , …

Относительная величина случайной погрешности косвенного измерения определяется в этом случае как

. (0.18)

Если распределения величин x_i, y_i, z_i, … нормальные (i - порядковый номер измерения), то распределение величины А_i тоже будет нормальным, поэтому для определения доверительной границы случайной погрешности косвенного измерения ∆А_гр можно применить метод обработки случайных погрешностей прямых измерений.

Для этого найдем значения

и (0.19)

для каждого номера измерений.

Аналогично формуле (0.2) находят величины ∆А_i:

(0.20)

Оценкой средней квадратической погрешности величины А аналогично формулам (0.8) и (0.10) будет

, (0.21)

если случайные погрешности заведомо больше приборных.

Доверительная погрешность ∆A_i при малом числе измерений (расчетов):

(0.22)

где - коэффициенты Стьюдента (см. табл.0.1) для заданных w и n.

Результат косвенного измерения величины А представляется в форме

A; ∆A от до ; w. (0.23)

После этого по формуле (0.18) находится относительная величина случайной погрешности.

В случае, если А = f(x, у, z,...) - логарифмируемая функция, то относительная погрешность может быть определена из следующих соображений: так как , то

(0.24)

Расчет погрешностей при графической обработке результатов измерений

В лабораторных работах 1, 2, 3, 11, 22, 23, 27, 44, 45 значения определяемых величин рассчитываются по угловому коэффициенту наклона к прямолинейного графика, построенного по экспериментальным точкам, к оси абсцисс. Прямую проводят таким образом, чтобы точки находились как можно ближе к ней. Соответствующая процедура в статистике называется линейной регрессией и сводится к определению коэффициентов к и b линейной зависимости вида у = кх + b по совокупности результатов наблюдений x₁, y₁; x₂, y₂; … x_n, y_n.

Расчет коэффициентов выполняется с помощью метода наименьших квадратов по формулам

(0.25)

(0.26)

Здесь , - средние арифметические значения величин х и у (см. формулу (0.1)), , и для n измерений могут быть рассчитаны следующим образом

; .

Для графика, построенного по коэффициентам, найденным по формулам (0.25) и (0.26), сумма квадратов расстояний по ординате от прямой до точек с координатами x_i и y_i оказывается наименьшей. При вычислении этой суммы индекс i последовательно принимает значения от 1 до n, где n - количество пар x_i , y_i результатов наблюдений.

Если графическая обработка результатов проведена достаточно аккуратно, то построенный график оказывается близким к оптимальному, а угловой коэффициент наклона графика мало отличается от коэффициента к, рассчитанного по методу наименьших квадратов. В этом случае для оценки погрешностей углового коэффициента наклона графика (к) и ординаты точки пересечения его с вертикальной осью (b) допустимо использовать выражения, применяемые при статистической обработке результатов по методу наименьших квадратов.

Среднее квадратическое отклонение углового коэффициента наклона графика к и коэффициента b

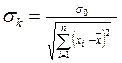(0.27)

(0.28)

Здесь , а y₀ - оценка среднего квадрата отклонения по ординате результатов наблюдений y_i от величин, рассчитанных по формуле y = kx + b с помощью вычисленных по методу наименьших квадратов коэффициентов:

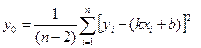. (0.29)

При графической обработке y₀ - это сумма квадратов вертикальных отклонений результатов наблюдений от построенной прямой, деленная на (п-2). Если делить на число наблюдений п, то получается заниженная, т.е. смещенная оценка среднего квадрата отклонения. Величина y₀ не зависит от количества наблюдений п, а , как следует из выражения (0.27), должна уменьшаться с возрастанием п. Для уменьшения погрешности величины к следует стремиться к увеличению ширины интервала значений х, это видно из формулы (0.27).

Если график отличается от оптимального, то сумма квадратов отклонений экспериментальных точек от прямой не будет наименьшей, возрастут величины y₀ и , как того и следует ожидать.

Доверительная граница случайной погрешности и относительная погрешность вычисляются по известным формулам (0.10) и (0.12):

; , (0.30)

где - коэффициент Стьюдента, определяемый по табл.0.1.

В некоторых работах требуется по графику определить координату хо точки пересечения графика с горизонтальной осью. Если коэффициенты k, b и их граничные погрешности определены, то рассчитывается, как погрешность косвенных измерений:

. (0.31)

Суммируя вышесказанное, приведем краткие рекомендации по расчету погрешностей графического метода определения коэффициентов к и b линейной зависимости у = кх + b.

1. Выбрать масштабы по осям так, чтобы разность максимальных и минимальных значений каждой величины была не менее 10 см.

2. Изобразить экспериментальные данные на графике точками, кружками или крестиками и провести прямую между точками так, чтобы расстояния от нее до экспериментальных точек были как можно меньше.

3. Выбрать на построенной прямой две достаточно удаленные друг от друга точки с координатами x_l, y_l, x_h, y_h и рассчитать коэффициент к по формуле:

4. Если необходимо, определить коэффициенты b и x₀- ординату и абсциссу точек пересечения прямой с OY и ОХ.

5. Измерить вертикальные отклонения экспериментальных точек от графика с учетом масштаба и определить величину у₀ по формуле (0.29).

6. Рассчитать среднее отклонение найденного углового коэффициента наклона к по формуле (0.27) и его граничную погрешность по формуле (0.30).

7. Если требуется, определить погрешности коэффициентов b и x₀ по формулам (0.28) и (0.31).

Правила приближенных вычислений

При физических измерениях принято писать только значащие Цифры, особенно в окончательном результате. При этом принято считать, что разряд сомнительной цифры числа совпадает с разрядом первой значащей цифры его абсолютной погрешности.

Числовые результаты удобно представлять следующим образом: ставить запятую после первой отличной от нуля цифры, а все число умножить на соответствующую степень десяти. Например: 21 000 = 2,1 10⁴; 0.00015 = 1,5∙10^-4.

Нуль в последнем разряде после запятой следует сохранять, если это верная или сомнительная цифра, незначащие нули отбрасывают.

Чтобы приближенно найти количество значащих цифр в числах, необходимо пользоваться следующими правилами:

1. Сложение и вычитание. Разряд сомнительной цифры суммы совпадает со старшим из разрядов сомнительных цифр всех слагаемых.

2. Умножение, деление, возведение в степень и извлечение корня. Результат любого из этих действий содержит столько значащих цифр, сколько их в исходном данном с наименьшим количеством значащих цифр.

3. Логарифмирование. Некоторое число и мантисса его логарифма содержат одинаковое количество значащих цифр.

4. Округление. Перед тем, как приступить к выполнению действия, нужно при помощи правил 1...3 определить количество значащих цифр (или разряд сомнительной цифры) результата и округлить исходные данные. После выполнения действия необходимо округлить результат, сохранив в нем только значащие цифры.

5. Правило запасной цифры. Чтобы по возможности уменьшить ошибки округления, рекомендуется в тех исходных данных, которые это позволяют, а также и в результате, если он будет использоваться в дальнейших вычислениях, сохранить по одной лишней (запасной) цифре сверх того, что требуют правила 1...4.