 |
|
пара параллельных плоскостей пара сливающихся плоскостей
ПП 7.5. Поверхности второго порядка
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
Эллипсоид
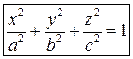
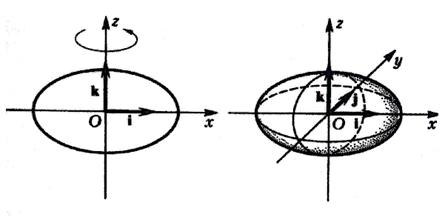
Гиперболоиды
Однополостный гиперболоид
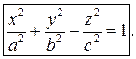

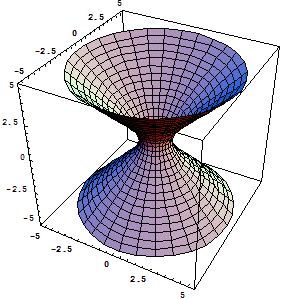
Двуполостный гиперболоид



Конус

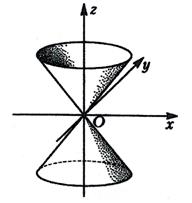

Эллиптический параболоид
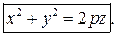
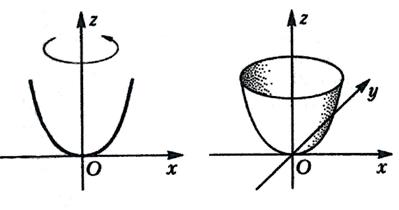
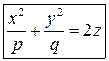

Гиперболический параболоид
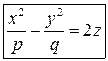


Цилиндры
Эллиптический
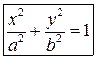
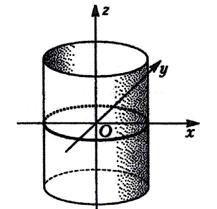
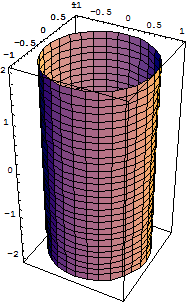
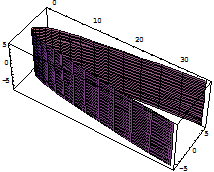
гиперболический  , параболический
, параболический 

.
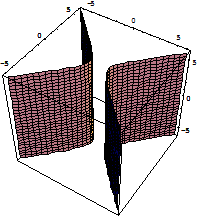
Пары плоскостей
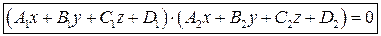

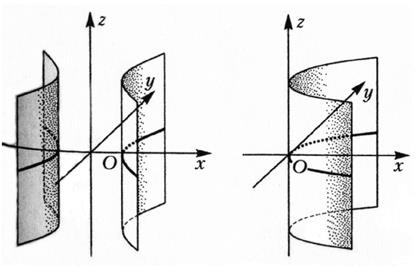
Пара пересекающихся плоскостей


пара параллельных плоскостей пара сливающихся плоскостей
| ПП 7.5. Поверхности второго порядка | ||
| ПП 7.5. №1. | Установите тип поверхности, заданной уравнением 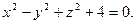 Решение:
Перенесем константу в правую часть уравнения и разделим обе части уравнения на число 4. Получим
Решение:
Перенесем константу в правую часть уравнения и разделим обе части уравнения на число 4. Получим
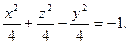 Это уравнение задает двуполостный гиперболоид вращения с осью OY.
Это уравнение задает двуполостный гиперболоид вращения с осью OY.
| Дву-полостный гиперболоид |
| ПП 7.5. №2. | Установите тип поверхности, заданной уравнением 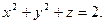 Решение:
Преобразуем уравнение к виду
Решение:
Преобразуем уравнение к виду
 являющемуся канонической формой уравнения параболоида вращения с осью OZ, вершина которого находится в точке (0;0;2), а выпуклость обращена вверх.
являющемуся канонической формой уравнения параболоида вращения с осью OZ, вершина которого находится в точке (0;0;2), а выпуклость обращена вверх.
| Параболоид |
| ПП 7.5. №3. | Установите тип указанной поверхности и постройте ее:
1)  ;
2) ;
2) 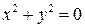 ;
3) ;
3) 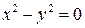 ;
4) ;
4)  ;
5) ;
5)  . .
| 1) параболоид вращения;
2) ось oz;
3) две пересекаю-щиеся плоскости 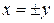 ;
4) две плоскости ;
4) две плоскости 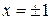 , параллельные плоскости zoy;
5) круговой цилиндр с образующей, параллельной оси oy. , параллельные плоскости zoy;
5) круговой цилиндр с образующей, параллельной оси oy.
|
| ПП 7.5. №4. | Составьте уравнения проекций на координатные плоскости сечения эллиптического параболоида
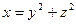 плоскостью
плоскостью
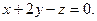 Решение:
Сечение параболоида плоскостью задается системой уравнений
Решение:
Сечение параболоида плоскостью задается системой уравнений
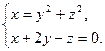 Этой системе соответствует некоторая линия в пространстве. Чтобы найти проекцию этой линии на координатную плоскость OXY, следует исключить из этой системы переменную z. В результате получаем
Этой системе соответствует некоторая линия в пространстве. Чтобы найти проекцию этой линии на координатную плоскость OXY, следует исключить из этой системы переменную z. В результате получаем 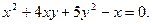 Аналогично находятся остальные проекции.
На плоскость OXY: Аналогично находятся остальные проекции.
На плоскость OXY: 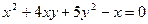 ; На плоскость OXZ: ; На плоскость OXZ: 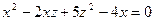 ; На плоскость OYZ: ; На плоскость OYZ:  . .
| 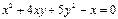  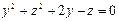
|
| ПП 7.5. №5. | Составьте уравнение поверхности, образованной вращением кривой
 вокруг оси OX.
Решение:
Сечение искомой поверхности плоскостью
вокруг оси OX.
Решение:
Сечение искомой поверхности плоскостью 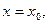 перпендикулярной оси вращения, есть окружность с центром в точке перпендикулярной оси вращения, есть окружность с центром в точке 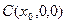 радиусом радиусом 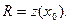 Уравнение этой окружности Уравнение этой окружности 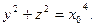 Для произвольного Для произвольного  получаем уравнение поверхности вращения получаем уравнение поверхности вращения 
| 
|
| ПП 7.5. №6. | Найдите общие точки поверхности  и прямой и прямой 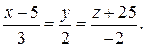 Решение:
Выделим полные квадраты переменных в уравнении поверхности и увидим,
что она представляет собой сферу
Решение:
Выделим полные квадраты переменных в уравнении поверхности и увидим,
что она представляет собой сферу  .
Перейдем к параметрическим уравнениям прямой .
Перейдем к параметрическим уравнениям прямой 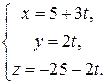 Подстановка этих значений переменных в уравнение поверхности приводит к квадратному уравнению для t c отрицательным дискриминантом. Следовательно, действительных значений t не существует, и поверхность не имеет общих точек с прямой, которая проходит вне сферы.
Подстановка этих значений переменных в уравнение поверхности приводит к квадратному уравнению для t c отрицательным дискриминантом. Следовательно, действительных значений t не существует, и поверхность не имеет общих точек с прямой, которая проходит вне сферы.
| Нет |
| ПП 7.5. №7. | Найдите общие точки поверхности 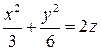 и плоскости и плоскости 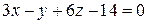 .
Решение:
Общие точки поверхностей удовлетворяют системе .
Решение:
Общие точки поверхностей удовлетворяют системе 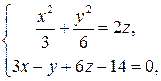 Приравнивая значения 2z , выраженные из этих уравнений, получим, что
Приравнивая значения 2z , выраженные из этих уравнений, получим, что 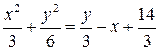 . Выделение полных квадратов переменных приводит к уравнению эллипса . Выделение полных квадратов переменных приводит к уравнению эллипса 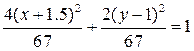 , который является линией пересечения эллиптического параболоида и плоскости. , который является линией пересечения эллиптического параболоида и плоскости.
| 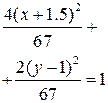
|
| ПП 7.5. №8. | Составьте уравнение цилиндра, образующие которого параллельны вектору 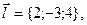 а направляющая задана уравнениями а направляющая задана уравнениями
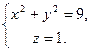 Решение:
Множество точек искомой поверхности образовано точками, лежащими на прямых, проходящих через некоторую точку направляющей параллельно вектору
Решение:
Множество точек искомой поверхности образовано точками, лежащими на прямых, проходящих через некоторую точку направляющей параллельно вектору 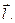 Составим канонические уравнения этих прямых: Составим канонические уравнения этих прямых:  Здесь M(x;y;z) - произвольная точка прямой, а N(X;Y;1) – фиксированная точка направляющей, через которую проходит прямая, называемая образующей. Отсюда Здесь M(x;y;z) - произвольная точка прямой, а N(X;Y;1) – фиксированная точка направляющей, через которую проходит прямая, называемая образующей. Отсюда
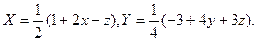 Подставим эти выражения в уравнение Подставим эти выражения в уравнение 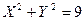 , которому удовлетворяют координаты точек направляющей и получим искомое уравнение цилиндрической поверхности: , которому удовлетворяют координаты точек направляющей и получим искомое уравнение цилиндрической поверхности: 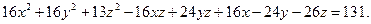
| 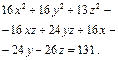
|
| ПП 7.5. №9. | Составьте уравнение конуса с вершиной в точке S(0;0;5) и направляющей
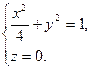 Решение:
Множество точек искомой поверхности образовано точками, лежащими на прямых, проходящих через некоторую точку направляющей и точку S. Составим канонические уравнения этих прямых
Решение:
Множество точек искомой поверхности образовано точками, лежащими на прямых, проходящих через некоторую точку направляющей и точку S. Составим канонические уравнения этих прямых  Здесь M(x;y;z) - произвольная точка прямой, а N(X;Y;0) – фиксированная точка направляющей, через которую проходит прямая, называемая образующей. Отсюда Здесь M(x;y;z) - произвольная точка прямой, а N(X;Y;0) – фиксированная точка направляющей, через которую проходит прямая, называемая образующей. Отсюда  Подставим эти выражения в уравнение Подставим эти выражения в уравнение 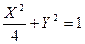 , которому удовлетворяют координаты точек направляющей, и получим искомое уравнение конической поверхности: , которому удовлетворяют координаты точек направляющей, и получим искомое уравнение конической поверхности: 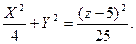
| 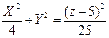
|
| ПП 7.5. №10. | Найдите общие точки поверхности 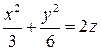 и плоскости и плоскости 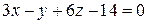 .
Решение:
Общие точки поверхностей удовлетворяют системе .
Решение:
Общие точки поверхностей удовлетворяют системе 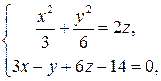 Приравнивая значения 2z , выраженные из этих уравнений, получим, что
Приравнивая значения 2z , выраженные из этих уравнений, получим, что 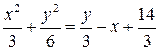 . Выделение полных квадратов переменных приводит к уравнению эллипса . Выделение полных квадратов переменных приводит к уравнению эллипса 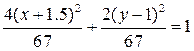 , который является линией пересечения эллиптического параболоида и плоскости. , который является линией пересечения эллиптического параболоида и плоскости.
| 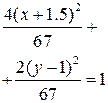
|
| ПП 7.5. №11. | Составьте уравнение сферы с центром в точке (3,-5,-2), если плоскость  касается сферы.
Решение:
Расстояние от центра сферы до касательной плоскости равно радиусу сферы: касается сферы.
Решение:
Расстояние от центра сферы до касательной плоскости равно радиусу сферы:
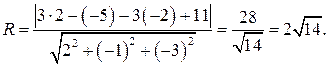 Уравнение сферы:
Уравнение сферы: 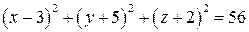 . .
| 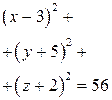
|
| ПП 7.5. №12. | Составьте уравнение сферы, проходящей через точки 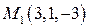 , , 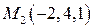 , , 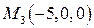 , центр которой лежит на плоскости , центр которой лежит на плоскости 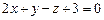 .
Решение:
Запишем уравнение сферы в виде .
Решение:
Запишем уравнение сферы в виде  и подставим в него координаты точек; кроме того, учтем, что центр сферы лежит на плоскости: и подставим в него координаты точек; кроме того, учтем, что центр сферы лежит на плоскости:
 Раскрывая скобки, получаем
Раскрывая скобки, получаем
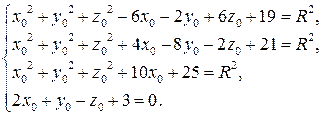 Вычитая из третьего уравнения второе и из второго первое, для координат центра сферы получаем равносильную систему
Вычитая из третьего уравнения второе и из второго первое, для координат центра сферы получаем равносильную систему
 откуда
откуда  и и  . Уравнение сферы . Уравнение сферы  . .
| 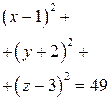
|
| ПП 7.5. №13. | Методом сечений исследуйте поверхность, заданную уравнением
 .
Решение:
Перепишем уравнение поверхности в виде .
Решение:
Перепишем уравнение поверхности в виде
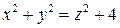 и рассмотрим сечения поверхности плоскостями
и рассмотрим сечения поверхности плоскостями 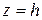 . В сечении получаются окружности с центром на оси . В сечении получаются окружности с центром на оси 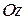 и радиусом и радиусом 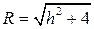 . Это позволяет заключить, что поверхность является поверхностью вращения с осью . Это позволяет заключить, что поверхность является поверхностью вращения с осью 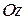 , и точки поверхности существуют при любых значениях , и точки поверхности существуют при любых значениях 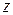 . Рассмотрим осевое сечение плоскостью . Рассмотрим осевое сечение плоскостью 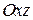 (или (или 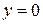 ): ):
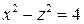 .
Приводя к каноническому виду, имеем .
Приводя к каноническому виду, имеем
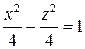 – уравнение гиперболы,
– уравнение гиперболы,  – действительная ось, – действительная ось, 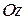 – мнимая ось.
Итак, поверхность может быть получена вращением гиперболы относительно ее мнимой оси, т.е. поверхность – однополостный гиперболоид вращения, – мнимая ось.
Итак, поверхность может быть получена вращением гиперболы относительно ее мнимой оси, т.е. поверхность – однополостный гиперболоид вращения, 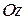 – ось симметрии, – ось симметрии, 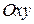 – плоскость симметрии. – плоскость симметрии.
| Однопо-лостный гиперболоид вращения |
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.