 |
|
Пусть искомая величина является функцией величин
Общая физика
Методические указания к выполнению лабораторных работ «Введение в теорию погрешностей измерений»
для студентов всех специальностей
Брянск 2004
Министерство образования РФ
Брянская государственная инженерно-технологическая академия
Кафедра физики
Утверждено научно-методическим советом БГИТА Протокол № от 2004 г.
Общая физика
Методические указания к выполнению лабораторных работ
«Введение в теорию погрешностей измерений»
для студентов всех специальностей
Брянск 2004
Составитель: Царьковская Н.И., к.т.н., доцент, кафедры физики
Сахаров Ю.Г. к.ф.-м.н., доцент кафедры физики
Рецензент: Баранова И.М., к.ф.-м.н., доцент, зав. кафедрой математики
Рекомендовано редакционно-издательской комиссией строительного факультета, протокол № от 2004 г.
1.ВВЕДЕНИЕ
Важнейшей задачей физического практикума является обучение будущих инженеров обработке результатов эксперимента. Значение любой величены, определенной опытным путем, содержит большую или меньшую погрешность. В науке и технике невозможно использовать численные значения величин без знания их погрешностей. Поэтому очень важно научиться правильно рассчитывать погрешность измеряемой величины, уметь анализировать условия измерения, находить источники погрешностей, оценивать возможности используемого измерительного оборудования. Это тем более важно, что точность измерений является одной из характеристик технического уровня производства. Важно планировать и проводить эксперимент так, чтобы точность окончательного результата соответствовала его цели.
Настоящее пособие является кратким руководством по математической обработке результатов измерений. Желающие ознакомиться с этим вопросом более подробно могут сделать это с помощью указанной в приложении литературы.
2.КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ И ИХ ПОГРЕШНОСТЕЙ
Измерение – это нахождение значения физической величены опытным путем с помощью специальных технических средств или путем расчетов.
Различают прямое и косвенное измерения физической величены.
Прямое измерение - измерение, при котором искомое значение величены находят опытным путем с помощью измерительных приборов.
Примерами прямых измерений могут служить: измерение длины с помощью линейки, штангенциркуля, микрометра; измерение временных интервалов секундомером; измерение силы электрического тока амперметром; измерение температуры термометром, термопарой.
Косвенное измерение – измерение, при котором для получения искомой величины требуется проведение математических операций над результатами прямых измерений, т.е. когда искомая величина задана в виде функции y = f (a, b, c …), где a, b, c… - независимые переменные, значения которых определяются прямыми измерениями.
Пример: В работе №2 необходимо определить величину ускорения, с которым движутся грузы под действием постоянной силы.
Для этого используют зависимость между величиной пути (S), ускорением движения грузов (а) и временем движения (t):

 ; (2.1)
; (2.1)

из нее получают формулу для ускорения


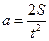 . (2.2)
. (2.2)
В результате прямых измерений определяют величину пути и время, за которое грузы проходят этот путь. По результатам прямых измерений (S и t) рассчитывают величину ускорения. Таким образом, в данной работе ускорение является величиной, найденной в результате косвенного измерения.
Результаты прямых измерений никогда не совпадают с истинным значением измеряемой величены. Это обусловлено принципиальными возможностями измерительных приборов, методов измерений, природой измеряемых объектов и воздействием окружающей среды. Поэтому любое прямое измерение проводят с определенной погрешностью.
Под погрешностью измерения понимают отклонение результата измерения от истинного значения измеряемой величины. По способу числового выражения различают абсолютные погрешности Δа, выраженные в единицах измеряемой величины, и относительные δ, выраженные в процентах. Погрешности вычисляются по следующим формулам:

ΔАi = аi - А (2.3)
 (2.4)
(2.4)
где аi – измеренное значение величины, А – истинное ее значение.
Погрешности делятся на три основных вида: систематические, случайные и промахи.
Систематические погрешности – погрешности, постоянные или изменяющиеся по определенному закону в зависимости от вызывающих их причин. Источниками систематических погрешностей обычно являются неправильная юстировка приборов, плохо обученный оператор, проводящий измерения, закономерно изменяющиеся внешние факторы, неправильный учет сопутствующих эффектов. Для выявления и исключения систематических погрешностей необходимо предварительно изучить источники погрешностей, провести контрольные проверки мер и измерительных приборов, обучить оператора правилам пользования измерительными средствами, использовать поправочные формулы, кривые, таблицы, исключить, если это возможно, источник той или иной погрешности (установить указатель прибора перед проведением измерений в нулевое положение, устранить источник температурных и других влияний).
Случайные погрешности – погрешности, неопределенные по значению и знаку, возникающие в результате совокупного действия различных случайных величин. Этот вид погрешностей обнаруживается при многократном измерении одной и той же величины в одинаковых условиях с помощью одних и тех же средств. Числовые результаты, получаемые при измерениях, всегда несколько отличаются друг от друга. Случайные погрешности нельзя исключить, их влияние на результат измерений следует учитывать методами теории вероятностей и математической статистики.
Промахи – результаты, резко выделяющиеся из данной серии измерений. Они возникают из-за неисправностей измерительной аппаратуры, ошибок в измерительных схемах, неправильных действий наблюдателя (неправильные записи наблюдений, неверный отсчет показаний измерительных приборов) и других причин. Результаты измерений, содержащие промахи, должны быть отброшены как недостоверные. Во избежание промахов перед проведением измерений нужно исключить создающие их причины и обращать особое внимание на соблюдение аккуратности и тщательности в работе с приборами и записями отсчетов.
3. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
ПРЯМЫХ ИЗМЕРЕНИЙ
3.1. Основы метода
Из опытных данных следует, что случайные погрешности определения физической величины в большинстве случаев подчиняются нормальному закону распределения (закону распределения Гаусса):
 (3.1)
(3.1)
где f(a) – функция плотности вероятности или функция распределения,
А – истинное значение измеряемой величины,
аi – значение измеряемой величины, полученное при i-том измерении,
σ2 – дисперсия распределения (является мерой рассеивания случайных величин),
σ – стандартное отклонение.
Общие свойства этого распределения:
1. Погрешности измерений могут принимать непрерывный ряд значений.
2. Вероятность появления случайных погрешностей, равных по абсолютной величине, но противоположных по знаку, одинакова.
3. Вероятность появления малых случайных погрешностей больше вероятности появления значительных (малые погрешности встречаются чаще, чем большие).
Вид функции f(а) показан на рис. 3.1.
Оценка случайной погрешности прямых измерений
Пусть величину А измеряли n раз и наблюдали при этом значения а1, а2, а3, …, аi, …, аn. Случайная абсолютная погрешность отдельного измерения
ΔАi = аi – А. (3.2)
Истинное значение А измеряемой величины почти всегда неизвестно, и поэтому определить погрешность каждого отдельного измерения по разности (3.2) не представляется возможным. Если число измерений n достаточно велико, то вместо значения А берут наиболее достоверное значение – среднее арифметическое серии измерений:
 (3.3)
(3.3)
Рис. 3.1. Распределение Гаусса
Зная среднее арифметическое значение, можно по аналогии с разностью (3.2) определить разность
 (3.4)
(3.4)
где Δаi – отклонение результата отдельного измерения от среднего значения. Это отклонение может быть вычислено для каждого измерения.
Из сравнения выражений (3.4) и (3.2) следует, что погрешности Δаi отличаются от случайных погрешностей ΔАi так, как отличается среднее арифметическое значение ряда измерений от истинного А – значения их близки друг к другу, но, как правило, не равны. Степень приближения Δаi к ΔАi будет тем больше, чем больше n, при n → ∞ можно считать, что
Δаi = ΔАi (3.5)
Следовательно при бесконечно большом числе измерений истинное значение измеряемой величины А равно среднему арифметическому ряда измерений А̃:
А = А̃. (3.6)
Однако при ограниченном числе измерений (n ≠ ∞) среднеарифметическое значение А̃ будет отличаться от А.
Задача состоит в том, чтобы каким-то образом оценить величину расхождения между средним значением измеренной величины и ее истинным значением, т.е. вместо равенства (3.6) записать:
А̃ - Δа ≤ А ≤ А̃ + Δа. (3.7)
Величина Δа – оценка абсолютной погрешности результата серии измерений остается пока неопределенной. Назовем доверительным интервалом интервал (А̃ - Δа; А̃ + Δа), в который, по определению, попадает истинное значение измеряемой величины с заданной вероятностью. Вероятность того, что среднее значение А̃ отличается от истинного на величину не более, чем Δа, называется доверительной вероятностью α (или коэффициентом надежности).
Это принято записывать в виде:
Р(А̃ - Δа< А <А̃ + Δа) = α. (3.8)
Из выражения (3.8) следует, что чем больше доверительный интервал, тем вероятнее, что результаты измерения не выйдут за его пределы и надежность будет выше. Очевидно, что при этом допустимая погрешность будет больше (точность измерения уменьшается).
Таким образом, для характеристики случайной ошибки необходимо задать два числа, а именно: величину самой ошибки (или полуширину доверительного интервала Δа) и величину доверительной вероятности (коэффициент надежности α), так как указание только погрешности делает результат неопределенным. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.
На практике степень надежности проводимых измерений зависит от их характера. При большенстве обычных измерений можно ограничиться доверительной вероятностью 0,9 или 0,95, если не требуется более высокая степень надежности. Вероятность определяется законом распределения погрешностей. Для нормального закона распределения средней квадратической ошибке, равной σ, соответствует значение доверительной вероятности 0,683; ошибке 2σ – 0,954; ошибке 3σ – 0,997.
Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратической ошибки. Средней квадратической ошибкой отдельного измерения называется величина:
 (3.9)
(3.9)
Для оценки погрешности результата всей серии из n измерений с заданным значением надежности α вводят понятие средней квадратической ошибки среднего арифметического S(А̃), определяемой по формуле:
 . (3.10)
. (3.10)
При малом числе измерений n закон распределения случайных величин несколько отличается от нормального (Гауссовского) и описывается распределением Стьюдента (псевдоним английского статистика Госсета). Для нахождения доверительного интервала Δа, в котором лежит результат серии измерений необходимо найденное значение S(А̃) умножить на коэффициент Стьюдента tαn:
Δа = tα,nS(А̃) (3.11)
Значение коэффициента Стьюдента tαn зависят от заданной доверительной вероятности α и числа измерений n и определяются по таблицам Стьюдента-Фишера.
Таблица 3.1
Значения коэффициентов Стьюдента для α = 0,95
| n | |||||||||
| tαn | 12,7 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,36 | 2,31 | 2,26 |
3.3. Доверительные границы неисключенной систематической погрешности результата измерения в соответствии с ГОСТ-8.207-76
Неисключенная систематическая погрешность результата образуется в общем случае из составляющих, в качестве которых могут быть неисключенные систематические погрешности: метода, средств измерений. В качестве границ неисключенной систематической погрешности в работах лабораторного практикума принимают пределы погрешностей средств измерений. Погрешность прибора указывают в паспорте прибора или ее можно вычислить, исходя из класса точности прибора.
Все электроизмерительные приборы разделяются на несколько классов точности:
0,05; 0,1; 0,2; 0,5; 1,0 и др.
Принадлежность прибора к данному классу точности характеризуется наибольшим допустимым значением приведенной погрешности γ, которая определяется по формуле
 , (3.12)
, (3.12)
где γ - приведенная погрешность в процентах,
аmax – максимальное значение показаний прибора (предел измерения),
Δаn – максимальная допустимая абсолютная погрешность прибора.
Абсолютная погрешность Δаn считается одинаковой для всей шкалы измерительного прибора, величину ее можно определить по формуле (3.12), зная предел измерения прибора и класс точности. Чем меньше отклонение стрелки прибора, тем выше относительная погрешность измеренной величины.
Пример: Миллиамперметром на 75мА измерен ток 3мА.Класс точности прибора 0,2, т.е. приведенная погрешность 0,2%.Это значит, что при измерении любого тока в пределах 0-75мА максимальная абсолютная погрешность равна:
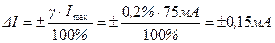 (3.13)
(3.13)
Следовательно, относительная погрешность измерения
 (3.14)
(3.14)
I - значение измеряемой величины.
Граница неисключенной систематической погрешности θ вычисляется по формуле :
 (3.15)
(3.15)
где k-коэффициент, определяемый принятой доверительной вероятностью. При доверительной вероятности α=0,95 коэффициент k принимают равным 1,1.
Для приборов, измеряющих механические величины, за неисключенную систематическую погрешность принимается половина цены деления шкалы. Например, шкала нониуса штангенциркуля имеет цену деления 0,05 мм. Следовательно, неисключенная систематическая погрешность определения линейных размеров будет составлять Δа = 0,025 мм
3.4 Границы погрешности результата измерения
В случае, если  , неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата
, неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата
 (3.16)
(3.16)
Если  , то случайной погрешностью по сравнению с систематической пренебрегают и принимают, что граница погрешности результата
, то случайной погрешностью по сравнению с систематической пренебрегают и принимают, что граница погрешности результата
Δ = θ. (3.17)
В том случае, если приведенные выше неравенства не выполняются, т.е.  необходимо учитывать вклады случайной и систематической погрешностей и границы погрешности результата измерения Δ вычисляют по формуле:
необходимо учитывать вклады случайной и систематической погрешностей и границы погрешности результата измерения Δ вычисляют по формуле:
Δ = КSΣ (3.18)
где К – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей и определяемый по формуле:
 (3.19)
(3.19)
SΣ – оценка суммарного среднего квадратичного отклонения результата измерения, вычисляемая по формуле:
 . (3.20)
. (3.20)
3.5. Форма записи результата измерения
Результат измерения следует представить в форме:
А = А̃ ± Δа при α = 0,95 (3.21)
При этом численное значение доверительного интервала не должно содержать больше двух значащих цифр, а числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δа.
3.6. Порядок операций при выполнении прямых измерений
При обработке результатов прямых измерений предлагается следующий порядок операций:
1. Результат каждого измерения записать в таблицу.
2. Вычислить среднее арифметическое значение из n измерений
 . (3.22)
. (3.22)
3. Найти погрешности отдельных измерений
∆ai = ai - Ã (3.23)
4. Вычислить среднюю квадратическую ошибку отдельного измерения
 (3.24)
(3.24)
5. Вычислить среднюю квадратическую погрешность серии измерений
 (3.25)
(3.25)
6. Произвести оценку наличия промахов в приведенной серии измерений, для чего среднюю квадратическую ошибку отдельного измерения умножить на коэффициент vi, значение которого зависит от заданной доверительной вероятности и числа измерений.
Таблица 3.2
Значения коэффициента vi в зависимости от числа опытов n
при доверительной вероятности α = 0,95
| n | ||||||||
| vi | 1,41 | 1,69 | 1,87 | 2,00 | 2,09 | 2,17 | 2,24 | 2,29 |
Величина отдельного результата измерений ai, лежащая за пределами интервала (А̃ ± vi · Sn) считается промахом и исключается. После этого необходимо уточнить значение среднего арифметического А̃ (п. 2) и повторить расчеты по пунктам 3, 4.
7. Задается значение доверительной вероятности α и при данном числе n измерений по таблице определить коэффициент Стьюдента tα,n.
8. Найти границы доверительного интервала по формуле (3.11); это и есть случайная погрешность серии измерений
Δа = tα,n· S(Ã). (3.26)
9. Произвести учет погрешности прибора:
а) найти абсолютную погрешность прибора
- для электроизмерительных приборов:
 (3.27)
(3.27)
- для штангенциркуля, микрометра и аналитических весов:
 , (3.28)
, (3.28)
где ЦД – цена деления шкалы прибора.
б) найти границы неисключенной систематической погрешности прибора
θ = кΔаn, к = 1,1 (3.29)
в) если  , то неисключенными систематическими погрешностями по сравнению со случайными пренебрегаем и граница погрешности результата определяется как
, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегаем и граница погрешности результата определяется как
Δа = tα,n · S(Ã) (3.30)
г) если  , то случайной погрешностью по сравнению с систематической пренебрегают, что граница погрешности результата
, то случайной погрешностью по сравнению с систематической пренебрегают, что граница погрешности результата
Δа = к·Δаn (3.31)
д) если приведенные в п.п. в) и г) неравенства не выполняются, учитывают вклады случайной и систематической погрешностей, и границы погрешности результата измерения вычисляют по формуле:
Δа = К·SΣ (3.32)
где 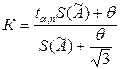 (3.33)
(3.33)
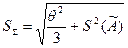 (3.34)
(3.34)
10. При определении массы взвешивание произвести 1 раз и за погрешность массы Δm взять произведение 0,5 массы наименьшего разновеса mmin на к (к = 1,1),
 (3.35)
(3.35)
11 Окончательный результат записывается в виде: а = А̃ ± Δа с доверительной вероятностью α = 0,95.
12 Оценить относительную погрешность результата измерений
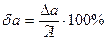 . (3.36)
. (3.36)
4. ОЦЕНКА ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
4.1. Теория метода
При косвенном измерении искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, поэтому само косвенное измерение не сопровождается появлением погрешностей. Величина погрешности косвенного измерения обусловлена «переносом» погрешностей результатов прямых измерений.
Пусть искомая величина является функцией величин
y = y(a1, a2, … an), (4.1)
где a1, a2, … an – аргументы, значения которых определяются прямыми измерениями;
Δa1, Δa2, … Δan – погрешности прямых измерений.
Необходимо оценить погрешность косвенных измерений Δy, зная погрешности прямых измерений Δаi с определенной надежностью α.
Абсолютная погрешность результата косвенных измерений определяется по формуле (которую приводим без вывода):
 (4.2)
(4.2)
или в более компактной форме:
 (4.3)
(4.3)
частные производные  в приведенном выражении вычисляются при средних значениях измеренных величин; Δаi (i = 1, 2, …, n) – величины погрешностей непосредственных измерений, вычисленные по формулам (3.30), (3.31), (3.32).
в приведенном выражении вычисляются при средних значениях измеренных величин; Δаi (i = 1, 2, …, n) – величины погрешностей непосредственных измерений, вычисленные по формулам (3.30), (3.31), (3.32).
Пример на применение формулы (3.30). Необходимо вычислить объем цилиндра
 (4.4)
(4.4)
Непосредственно определяется диаметр d и его высота h со своими погрешностями. Кроме того, π – иррациональное число, при округлении которого мы допускаем некоторую погрешность округления Δπ. В теории ошибок рекомендуется брать в постоянных столько знаков, чтобы ошибка округления была значительно меньше ошибок прямых измерений. Критерием служит следующее: относительная ошибка округления должна быть на порядок меньше относительной ошибки прямых измерений:

В этом случае погрешностью констант пренебрегают.
Предположим, что мы взяли π с таким числом знаков, что указанное условие выполняется.
По формуле (4.3) определяем ошибку измерения объема цилиндра:
 (4.5)
(4.5)
 (4.6)
(4.6)
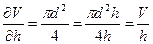 (4.7)
(4.7)
 (4.8)
(4.8)
Относительная погрешность объема цилиндра определяется по формуле:
 (4.9)
(4.9)
где δd и δh – относительные погрешности прямых измерений.
Допустим, что в результате прямых измерений мы получили значения:
| d = 12,8 ± 0,1 мм | при | α = 0,95 |
| h = 38,7 ± 0,1 мм | при | α = 0,95 |
Подставляя значения d̃ и h̃ в формулу (4.4) получим среднее арифметическое значение объема:

Рассчитываем:


Относительную погрешность 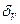 определим по формуле (4.9):
определим по формуле (4.9):




Окончательный ответ:

Часто в формулу косвенного измерения входят величины, которые берутся из справочников. Например: ускорение свободного падения, плотность веществ, удельные теплоемкости, заряд электрона и т.д. В справочниках даются обычно все верные цифры, поэтому ошибка округления равна половине следующего за последней цифрой разряда. Например, плотность стали ρ = 7.8 г/см3. Следовательно, Δρ = 0,05 г/см3 и относительная ошибка  . Если относительная ошибка справочных величин на порядок меньше относительной ошибки непосредственно измеренных величин, то ее подсчитывать не нужно. Рекомендуется пользоваться такими справочными данными, чтобы это условие выполнялось.
. Если относительная ошибка справочных величин на порядок меньше относительной ошибки непосредственно измеренных величин, то ее подсчитывать не нужно. Рекомендуется пользоваться такими справочными данными, чтобы это условие выполнялось.
4.2. Порядок операций при обработке косвенных измерений
1. Для всех непосредственно измеряемых величин, входящих в формулу для определения искомой величины, обработка проводится по п. 3.6. При этом для всех измеряемых величин задают одно и то же значение доверительной вероятности α.
2. Рассчитывается искомая величина
 (4.10)
(4.10)
при средних значениях непосредственно измеренных параметров  .
.
3. Оцениваются границы доверительного интервала для результата косвенных измерений по формуле (4.3):
 (4.11)
(4.11)
где производные  вычисляются при
вычисляются при  и т.д.
и т.д.
4. Окончательный результат записывается в виде
 (4.12)
(4.12)
при доверительной вероятности α = 0,95. Запись означает, что с вероятностью α истинное значение искомой величины y находится в интервале  .
.
5. Определяется относительная погрешность результата серии косвенных измерений
 . (4.13)
. (4.13)
5. ПОСТРОЕНИЕ ГРАФИКОВ
Аргумент (независимая переменная) откладывается вдоль оси х, функция (зависимая от х переменная) – вдоль оси y. Вначале нужно выбрать масштаб по осям координат. Масштаб выбирается таким образом, чтобы зависимости занимали практически все поле графика. Через каждые 10-20 мм наносятся на координатные оси масштабные деления данной физической величины кратные 1, 2, 5, 10 и т.д. Около каждой оси следует написать обозначение этой физической величины и ее размерность. Если численное значение данной физической величины имеет множитель  , то этот множитель необходимо вынести в обозначение оси. Например, в лабораторной работе №2 зависимость пути от времени при равноускоренном движении
, то этот множитель необходимо вынести в обозначение оси. Например, в лабораторной работе №2 зависимость пути от времени при равноускоренном движении 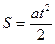 принимает линейный характер в осях S = f(t2). В лабораторной работе №9 чисто адиабатный процесс будет протекать при времени выпуска воздуха из баллона t = 0, что получается экстропаляцией линейного графика в осях lgh = f(t) к нулю времени, где h – показания U – образного манометра после выпуска воздуха. В лабораторной работе №49 проверка закона Столетова для фотоэффекта подтверждается линейным характером графика в осях
принимает линейный характер в осях S = f(t2). В лабораторной работе №9 чисто адиабатный процесс будет протекать при времени выпуска воздуха из баллона t = 0, что получается экстропаляцией линейного графика в осях lgh = f(t) к нулю времени, где h – показания U – образного манометра после выпуска воздуха. В лабораторной работе №49 проверка закона Столетова для фотоэффекта подтверждается линейным характером графика в осях  , где Iнас – максимальное значение фототока, r – расстояние от осветителя до фотоэлемента.
, где Iнас – максимальное значение фототока, r – расстояние от осветителя до фотоэлемента.
Экспериментальные точки наносятся в виде маленьких точек, обведенных кружком малого радиуса или треугольником, квадратиком и т.п. Линия графика внутри этих кружков не проводится. Если для экспериментальных точек известны погрешности измерения, то они указываются в виде вертикальных черточек соответствующей длины.
С помощью линейки, лекала или «от руки» между экспериментальными точками проводят гладкую кривую таким образом, чтобы примерно суммарное расстояние от точек до этой кривой было минимальным. Если имеются несколько кривых, то точки каждой кривой должны отличаться. Каждой кривой присваивается номер, а в подписи к графику указывают название, обозначение, цифровые значения и единицу измерения параметра, соответствующего этому номеру. Можно разные кривые чертить различным цветом. В качестве примера см. рис. 5.1, иллюстрирующий содержание данного параграфа на примере лабораторной работы №2 из физпрактикума.
Под графиком делается подпись, разъясняющая смысл этого графика. Многие физические законы на графиках с равномерными шкалами изображаются сложными кривыми. Для их упрощения, а чаще всего для их спрямления, применяют функциональные шкалы.
Рис. 5.1. График зависимости пути, пройденного грузом
от квадрата времени 
m1 = 5г; m2 = 10 г; m3 = 15 г.
Например, зависимость типа:  изображается прямой линией, если на оси абсцисс использовать равномерную шкалу для величины х, а на оси ординат – логарифмическую шкалу для величины y, тогда зависимость принимает вид
изображается прямой линией, если на оси абсцисс использовать равномерную шкалу для величины х, а на оси ординат – логарифмическую шкалу для величины y, тогда зависимость принимает вид  . Такая шкала называется полулогарифмической. Как видно из приведенного уравнения, на таком графике зависимость изобразится прямой линией, отсекающей на оси ординат отрезок, равный lnс, а тангенс угла наклона дает возможность определить постоянную α. Так же часто используются логарифмические шкалы, для определения степенной зависимости.
. Такая шкала называется полулогарифмической. Как видно из приведенного уравнения, на таком графике зависимость изобразится прямой линией, отсекающей на оси ординат отрезок, равный lnс, а тангенс угла наклона дает возможность определить постоянную α. Так же часто используются логарифмические шкалы, для определения степенной зависимости.
6. Метод наименьших квадратов
При проведении эксперимента часто измеряют пары величин х и у, при чем одна из них является функцией другой величины, например, у = f (х). Затем найденные значения откладывают на графике и пытаются найти кривую, соответствующую алгебраической функции у = f (х), которая проходила бы как можно ближе к точкам. Из теории вероятностей следует, что наилучшим приближением будет такая зависимость, для которой сумма квадратов расстояний по вертикали от каждой экспериментальной точки до кривой, будет минимальной.
Ограничимся случаем линейной зависимости у = kx+ b. Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно выбирают величины, откладываемые по осям, таким образом, чтобы получить прямую линию. Например, график пути от времени при равноускоренном движении строят в осях S = f (t2), частоту собственных колебаний струны от натяжения струны (Р) – в осях  , энергетическую светимость тела от его температуры (Т) – в осях Re = f(T4).
, энергетическую светимость тела от его температуры (Т) – в осях Re = f(T4).
Рассмотрим математическую сторону вопроса о нахождении наилучших значений углового коэффициента k и параматра b. При выводе предположим, что ошибки содержат только величины yi (такое предположение часто оправдывается на практике), иначе анализ весьма усложнится. Отклонение экспериментального значения yi от искомой линейной зависимости в i – том (i = 1, 2 … n) измерении, то есть при х = хi, составит
di = yi – (kxi + b) = yi – kxi – b (6.1)
Наилучшие значения k и b выбираются таким образом, чтобы сумма квадратов этих отклонений по всем n измерениям
 (6.2)
(6.2)
была минимальной; отсюда и наименование – метод наименьших квадратов. Для нахождения значения k и b, при которых величина S минимальна, приравниваем к нулю частные производные от S по k и b:
 , (6.3)
, (6.3)
 . (6.4)
. (6.4)
Искомые величины k и b получаются решением системы уравнений

Второе уравнение показывает, что наилучшая прямая проходит через точку с координатами
 (6.7)
(6.7)
то есть через центр тяжести всех экспериментальных точек. Из уравнений (6.5) и (6.6) находим угловой коэффициент k и параметр b:
 (6.8)
(6.8)
 (6.9)
(6.9)
Мера качества приближения – средние квадратичные отклонения величин k и b. Они имеют вид:
 (6.10)
(6.10)
 , (6.11)
, (6.11)
 . (6.12)
. (6.12)
Очевидно, что ручная обработка результатов с помощью приведенных формул достаточно трудоемка. Однако применение компьютеров при обработке позволяет использовать этот достаточно мощный метод. В программах к лабораторным работам №№ 3, 5, 9 применение метода наименьших квадратов позволяет строить графические зависимости и находить искомые значения с повышенной точностью. При построении графиков «вручную» метод наименьших квадратов используется интегрировано, на глаз проводится прямая между экспериментальными точками.
6. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
Ошибка результата определяется не только ошибкой измерений, но и ошибками вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого вспомним правила математических действий с приближенными числами.
Результаты измерений – приближенные числа. В приближенном числе все цифры должны быть верными. Последней верной цифрой приближенного числа считается та цифра, ошибка в которой не превышает одной единицы ее разряда. Все цифры от 1 до 9 и нуль, если он стоит в середине или в конце числа, называются значащими. В числе 6100 – четыре значащих цифры, а в 6,1·103 – только две, в числе 0,00209 – три, т.к. нули слева от двойки незначащие.
Запись 2,39 означает, что верны все знаки до второго после запятой, а запись 2,3900 – что верны также и третий и четвертый знаки. В числе 6,30 три значащие цифры и это значит, что при измерении мы учитывали не только единицы, но и десятые и сотые, в числе 6,3 – только две значащие цифры и это значит, что мы учитывали только целые и десятые и точность этого числа в десять раз меньше.