 |
|
Нахождение площади криволинейной трапеции
РАЗДЕЛ 1. ОпределЕнный интеграл
§ Основная задача интегрального исчисления –
нахождение площади криволинейной трапеции
Постановка задачи: Найти площадь фигуры, ограниченной снизу замкнутым промежутком оси абсцисс I = [a,b] (y= 0), слева – вертикальной прямой x = a , справа – вертикальной прямой x= b и сверху – дугой графика функции y = f (x). Такая фигура называется криволинейной трапецией опирающейся на промежуток I .
Несколько слов о понятии площади. Студенты с большим трудом и невнятно формулируют понятие площади. И не мудрено. В программе школьного образования не формулируется понятие площади, и оно остается чисто интуитивным. На самом деле площадь это некоторая функция 
, заданная на геометрических объектах 
и такая, что: 1) 
и 2) 
.
Теперь займемся решением поставленной задачи. Для этого поступим следующим образом:
А. Разобьём промежуток I на n частей, не обязательно равных по длине, точками 
: 
, и обозначим
– промежутки разбиения. Величину 
назовем диаметром промежутка разбиения, а величину 
– мерой промежутка разбиения.
При этом: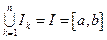 
и
. Для интервала понятие меры и диаметра не отличаются. Для произвольного множества самое большое из расстояний между элементами множеств, конечно, не всегда не совпадает с суммарной длиной интервалов, его составляющих.
Пусть 
– внутренность промежутка разбиения: =( 
) т.е. 
. При этом говорят: Задано разбиение Р = 
промежутка I = [a, b], а величина 
называется параметром разбиения Р.
Б. Теперь для каждого 
выберем точки 
т.е. 
.
Получаем 
разбиение с отмеченными точками.
В. Построим сумму площадей образовавшихся прямоугольников: 
, и перейдем к пределу при параметре разбиения, стремящемся к нулю. Если такой предел существует, то он называется определенным интегралом от функции 
по промежутку 
и для неотрицательной функции является площадью криволинейной трапеции.
.
Если функция является знакопеременной то определенный интеграл это, вообще говоря, не площадь а ориентированная площадь, когда считается, что фигуры лежащие выше оси абсцисс имеют положительную площадь, а фигуры лежащие ниже оси абсцисс имеют отрицательную площадь.
Свойства разбиений
Говорят, что разбиение Р мельче чем разбиение 
(или крупнее Р), (или Р следует за ) и записывают 
, если все точки разбиения содержатся среди точек разбиения Р. Отметим три важных свойства отношения «крупнее – мельче» для разбиений:
а) существуют разбиения со сколь угодным малым параметром:
I = [a, b]. Выбирая 
; k = 0,1,2,…,n. Тогда 
и выбирая 
достаточно большим, можно сделать параметр разбиения сколь угодно малым.
б) для двух любых разбиений 
существует третье разбиение, следующее за любым из них: 
с) транзитивность отношения «крупнее – мельче»:
и, что то же самое P1 É P2 Ù P2 É P3 Þ P1 É P3.
§ Определение определённого интеграла на языке 
.
Предел по базе
Def: Величина I (f ) называется определённым интегралом от функции f на промежутке [a, b] 
D(f ), если: 
.
Def: Если в множестве X задана система B подмножеств B множества X такая, что:
а) "BÎB B ¹ Æ; б) "B1, B2ÎB $B3ÎB B3 Ì B1∩B2,
то говорят, что в множестве X задана база.
Примеры.
1˚.Множество открытых окрестностей точки а образуют базу. Обозначим эту базу P 
.
2˚.Множество открытых проколотых окрестностей точки а образуют базу (P 
).
3˚.Множество открытых окрестностей точки а на плоскости образуют базу(P ).
4˚.Множество открытых проколотых окрестностей точки а на плоскости образуют базу(P ).
5˚.Множество всех разбиений промежутка [a, b] образуют базу (P 
)..
6˚.Множество всех разбиений промежутка [a, b] с параметром разбиения lP < d образуют базу.
7˚.Множество всех разбиений промежутка [a, b] с отмеченными точками образуют базу.
6˚.Множество всех разбиений промежутка [a, b] с отмеченными точками с параметром разбиения lP < d образуют базу. Последние три базы обозначают базу P 
или 
.
Def: 
. Пределом функции f (x) по базе B называется число А, такое, что:
. и тогда определение определенного интеграла может быть записано через предел по базе разбиений с отмеченными точками с параметром разбиения lP < d: 
.