 |
|
Критерий Дарбу интегрируемости функций по Риману
Т°. Функция f (x) интегрируема на промежутке [a, b], тогда и только тогда, когда её
верхний и нижний интегралы Дарбу равны между собой.
Û 
Û 
.
∆. а). Пусть функция 
интегрируема по Риману. Тогда
Û 
.
Следовательно: 
и, в силу того, что и верхняя и нижняя суммы Дарбу есть частные случаи сумм Римана, получим 
. Переходя к пределу при 
получаем, что 
, т.е.
.
б). Пусть верхний и нижний интегралы Дарбу совпадают. Принимая во внимание, что 
и используя теорему о двух милиционерах, переходим к пределу при : 
. ▲
Другие формулировки того же критерия:
*). Если интегрируема на 
, то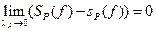 
.
*). Если интегрируема на , то 
.
Интегрируемость непрерывных и монотонных функций
Т°. Функция непрерывная на замкнутом промежутке интегрируема на нём.
.
Т°. Функция монотонная на замкнутом промежутке интегрируема на нём.
Þ .
∆ а). Пусть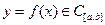 
т.е. непрерывна Þ равномерно непрерывна на . Тогда 
, и получим:
и по критерию Дарбу 
, что и требовалось доказать.
б). Пусть f (x) монотонна на [a, b]. Например, монотонно возрастающая: 
.
Тогда: 
, что и требовалось доказать.
Интегрируемость суммы, произведения и частного
Интегрируемых функций
1°. 
∆ Отметим, что f (x) и g(x) – ограничены на [a, b].
, 
.
Отсюда следует, что 
и, следовательно:
что, по критерию Дарбу, означает интегрируемость суммы двух (а значит и любого конечного числа) интегрируемых функций.
2°. 
.
∆ Пусть f (x), g(x) – ограничены.
= 
.
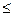
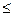
Значит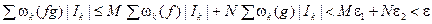 
, что, по критерию Дарбу, означает интегрируемость произведения двух (а значит и любого конечного числа) интегрируемых функций.
3°. 
и g(x) – отделена от нуля Þ 
.
∆ Достаточно доказать интегрируемость функции 
:
.
Здесь мы воспользовались тем, что g(x) отделена от нуля, т.е. | g(x) | ³ m > 0 и 
и, по критерию Дарбу, функция интегрируема.
Функция 
интегрируема, как произведение интегрируемых функций 
и 
.