 |
|
Критерий Лебега интегрируемости функции по Риману.
T°. Функция f (x) интегрируема по Риману на [a, b] тогда и только тогда, когда она
ограничена и непрерывна почти всюду на [a, b].(п.в. на [a, b]), т.е. множество её точек
разрыва имеет лебегову меру ноль.
Def: Множество М имеет лебегову меру ноль ( m(M) = 0 ) если существует не более чем счётная система промежутков, покрывающая множество М иимеющая сколь угодно малуюсуммарную меру т.е. "e > 0 ${In}nÎNÌℕ 
.
Промежутки In – будем считать открытыми, хотя это всё равно.
При этом:
1). Точка и конечное множество точек имеет лебегову меру ноль.
2).Счётное число точек имеет лебегову меру ноль. 
.
3). Всякое подмножество множества лебеговой меры ноль имеет лебегову меру ноль.
4). Объединение не более чем счётного числа множеств лебеговой меры ноль имеет лебегову
меру ноль.
5). Невырожденный промежуток не имеет лебеговой меры ноль и не может быть покрыт не более чем счётной системой промежутков с суммарной мерой меньшей его длины.
6). Множество лебеговой меры ноль не может иметь внутренних точек.
7). Существуют несчётные множества лебеговой меры 0.
D Для построения такого множества рассмотрим отрезок 
.
На первом шаге разделим отрезок на три равные части и удалим из отрезка средний интервал 
длиной 
. После первого шага останется два отрезка 
и 
. На следующем шаге с каждым из двух отрезков и поступим так же, как на первом шаге поступили с исходным отрезком т.е. выбросим еще два интервала длиной по 
. После второго шага останется четыре отрезка 
, 
, 
, 
. На рисунке изображены первые четыре шага построения искомого множества. Продолжим эту процедуру до бесконечности.
Множество точек, которые останутся после проведения описанной процедуры, называется канторовыммножеством.
Мера построенного канторового множества С равна 
. Итак, канторово множество имеет лебегову меру ноль. Докажем, что это множество не счетно.
Для этого представим каждое число, входящее в множество, в виде двоичной дроби, у которой целая часть равна нулю, первой цифрой после запятой является 1 или 3, в зависимости от того находится точка на левом или правом из трех промежутков, на которые разбит промежуток на первом шаге проделанной процедуры, вторая цифра после запятой это вновь 1 или 3, в зависимости от того находится точка на левом или правом из трех промежутков, на которые разбиты соответствующие подпромежутки на втором шаге проделанной процедуры, и т.д.
Тогда каждому элементу канторового множества поставлено в соответствие число вида 
, где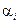 
это 1 или 3. Покажем что множество таких дробей не счетно. Доказательство проведем от противного. Допустим множество счетно, т.е. все его элементы можно занумеровать. Пусть эти числа занумерованы:
1). 
, 2). 
, 3). 
, 4). 
, …..
Здесь нижний индекс означает номер цифры после запятой, а верхний – номер, который получило число при данном способе нумерации. Тогда число 
, у которого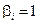 
, если 
и наоборот, не совпадает ни с одним из пронумерованных чисел, хотя и является числом того же типа. Противоречие доказывает что канторово множество не счетно. ▲