 |
|
Равномерная непрерывность функции на множестве.
Def: Величина 
называется колебанием функции 
на множестве М.
Def: Функция называется равномерно непрерывной на множестве М, если
.
Теорема Кантора: Функция непрерывная в ограниченной замкнутой области D равномерно непрерывна на D.
Δ. От противного. Возьмем числовую последовательность 
, такую что:
и ни одно из этих 
не годится для равномерной непрерывности.
Тогда 
, такая что 
, но 
. (*)
Получаем последовательность 
. Из этой последовательности выделим сходящуюся подпоследовательность 
. Для нее 
, в силу замкнутости области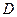 
. Так как 
, то при 
.
Значит, в силу непрерывности, 
, значит 
, что противоречит (*). ▲
Следствие:Если равномерно непрерывна в ограниченной замкнутой области D, то 
, таких, что 
– замкнуты, 
и 
выполнено: 
.
Δ В качестве 
достаточно взять это число из равномерной непрерывности.
Тогда 
. ▲
§. Компактные множества в Еn.
Def: Пусть 
и имеется система множеств 
= 
такая, что
. Тогда система множеств = называется покрытием множества М.
Тº. (Бореля). «Если ограниченное замкнутое множество D покрыто системой = открытых множеств, то из этого покрытия всегда можно выделить конечное.
Δ. От противного. Для наглядности иллюстрации и не ограничивая общности доказательство проведем в двухмерном пространстве. Пусть из существующего бесконечного покрытия нельзя выделить конечное. Проведем процедуру разбиения множества D на прямоугольники с последующим выбором из 4х прямоугольников одного, который не покрывается конечным покрытием…. Продолжая эту процедуру достаточно долго можно получить сколь угодно маленькие прямоугольники.
На некотором, к-ом шаге, мы придем к прямоугольнику Мк который содержит ту часть D, которая не покрыта конечным покрытием. Данная последовательность прямоугольников стягивается в точку 
. Эта точка 
, т.к. область D – замкнута. Тогда точка входит в одно из 
множеств покрытия. Так как - открытое множество, то входит в вместе с некоторой своей окрестностью.
В эту окрестность, при достаточно большом k, попадет и прямоугольник Мк, который нельзя покрыть конечным покрытием с одной стороны, а с другой стороны 
.▲
Def: Множество называется компактом, если из любого его бесконечного покрытия открытыми множествами можно выделить конечное покрытие.
Лемма Бореля показывает, что в Еn любое ограниченное замкнутое множество является компактом.