Главная | Обратная связь

Дифференциалы высших порядков.

 

Определение n дифференциала индуктивное: .

Пусть Тогда:

Найдем второй дифференциал. =

= =

=

= +

+ .

Для второго дифференциала получена формула:

В этой формуле выражение в квадратных скобках в правой части отсутствует, если – независимые переменные, и присутствует если

Это показывает, что форма второго дифференциала не инвариантна относительно замены переменных.

Формула для формального запоминания второго дифференциала для функции n независимых переменных имеет вид: .

а для дифференциала k^-го порядка:

 

Замечание: Обратим внимание на то, что если функции линейны т.е. имеют вид то второй дифференциал и более дифференциалы более высокого порядка инвариантны по форме.

 

Формула Тейлора.

 

Напоминание: Для функции одного переменного F(t) ранее была получена формула ее разложения в ряд Тейлора (по формуле Тейлора) в дифференциальной форме:

, где величина .

 

При этом, – в левой части и dt ­– в правой части совпадают.

В этом виде формула Тейлора справедлива и для функций нескольких переменных.

В дальнейшем, для упрощения письма ограничимся рассмотрением функции двух переменных .

 

Т°. Пусть u = f (x,y) определена и непрерывна в некоторой окрестности точки и имеет в этой окрестности непрерывные производные до (n+1)^-го порядка включительно. Пусть и таковы, что точка принадлежит указанной окрестности.

Тогда: =

= , где . При этом в левой части, совпадают с dx и dy в правой части.

 

Δ. Соединим точки Р и Р₀ прямолинейным отрезком, принадлежащим упомянутой в формулировке теоремы, окрестности: ; ; .

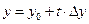Подставляя это в , получим .

Тогда: =

= , где .

 

При этом dt в правой части равенства равно Δt =1–0 =1.

 

Теперь воспользуемся тем, что при линейной замене переменных высшие дифференциалы инвариантны по форме. (*)

 

 

Аналогично для , ,…, и .

Подставляя в формулу (*) получаем требуемое. ▲