Главная | Обратная связь

Определение кратного интеграла

РАЗДЕЛ 10. Кратные интегралы.

НАЧАЛЬНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

 

Def. Пусть , , .

Множество называется замкнутым промежутком или замкнутым брусом в .

Множество называется открытым промежутком

или открытым брусом в .

Def. Мерой промежутков и называется величина:

( Точнее ).

Def. Если такое, что то промежуток называется вырожденным и .

Свойства меры промежутка:

а). Положительность: , причем тогда и только тогда, когда – вырожден.

б). Положительная однородность: .

в). Аддитивность:

* для таких, что Þ ;

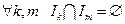* для и Þ .

г). Монотонность меры: .

 

Def. Диаметром бруса (промежутка) называется величина:

Отметим, что и – это не одно и тоже. Например, если – вырожден, то , a (вообще говоря).

При этом: * ;

* ; * .

Def. Совокупность подпромежутков промежутка называется разбиением промежутка , если: * ;

* ; * ; * ; * .

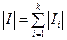Величина называется параметром разбиения P (при этом ).

 

Def. Разбиение называется измельчением разбиения 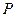, если все элементы разбиения получены разбиением элементов разбиения .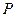

Обозначается: . Читается: мельче 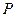или 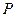крупнее .

Для отношения “ крупнее – мельче” справедливо:

*. транзитивность – ; *. ;

*. ; *. | .

 

Определение кратного интеграла

 

Пусть – брус (промежуток) в , – разбиение промежутка I. На каждом из промежутков разбиения отметим точку .

Получим 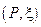разбиение с отмеченными точками для .

Величина называется интегральной суммой Римана для функции f (x) на промежутке I по разбиению с отмеченными точками .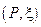

 

Def: = = .

 

Обозначая – множество функций интегрируемых на брусе I запишем:

Def: 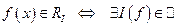ε > 0 δ > 0 < .

 

Если для функции f (x) на I и разбиения – обозначить через – наибольшее и наименьшее значение функции f (x) на I_k то величины = 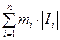и = называются нижней и верхней суммами Дарбу.

 

§. Критерий Дарбу существования кратного интеграла.

 

Т⁰. Чтобы функция была интегрируема на брусе (т.е. ) необходимо и достаточно, чтобы . Δ▲.

 

Определено интегрирование функции по брусу в евклидовом пространстве. А как функцию проинтегрировать по произвольному ограниченному множеству из евклидового пространства?

 

Определим интеграл от функции f по множеству .

Def: Пусть 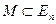и 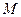– ограничено, т.е. . Функцию назовём характеристической функцией множества M .

Тогда: ≡ .

Определение интеграла по множеству не зависит от того, какой брус, содержащий М выбран, т.е. .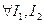

Это обозначает, что определение интеграла по множеству корректно.

 

Необходимое условие интегрируемости.Чтобы функция f (x) на М была интегрируемой необходимо, чтобы f (x) была ограниченной на М. Δ▲.