Главная | Обратная связь

ЗАМЕНА ПЕРЕМЕННЫХ В КРАТНЫХ ИНТЕГРАЛАХ.

1⁰.В одинарном интеграле: .

2⁰.В двойном интеграле:

.

3⁰.В тройном интеграле: =

= .

4⁰.В кратном интеграле: если , , и , то

.

Примеры:

1⁰. Вычислить двойной интеграл: .

Область интегрирования – круг единичного радиуса с центром в начале координат.

a). В декартовой системе координат: .

Недостатки: пределы интегрирования не красивые и, кроме того, интеграл не выражается через элементарные функции.

б). В полярной системе координат:

.

При переходе в полярную систему координат не только получился повторный интеграл с удобными пределами интегрирования, но, с учетом того, что внутренний интеграл не зависит от получилось даже произведение двух интегралов Римана.

 

2⁰. Вычислить , если область D – замкнутая часть плоскости ограниченная кривыми: {y = 2x; y = 4x; xy = 1; xy = 3}.

a). Расставлять пределы интегрирования в декартовой системе координат

расставлять очень не удобно. Поэтому сделаем по другому.

б). Сделаем замену переменных: u = xy, v = ; 1 ≤ u ≤ 3, 2 ≤ v ≤ 4.

Для выполнения замены переменных необходимо найти якобиан . Однако находить его неудобно. Поэтому воспользуемся соотношением: . Тогда 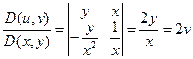. Якобиан положителен, следовательно, ориентация двух систем координат совпадает. И далее:

=…

 

3⁰. Вычислить интеграл .

I = Þ . Для нахождения полученного двойного интеграла перейдем в полярную систему координат.

= .

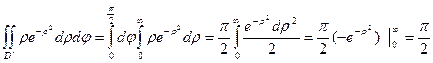
Тогда: . Пример показывает что не только двойной интеграл вычисляется с помощью перехода к повторным, но и наоборот.

 

§. Криволинейные интегралы 1^го рода.

Def : Если в Е₃ задана вектор-функция , и при этом x(t), y(t), z(t) C_[a,b], C¹_[a,b] , то говорят, что в Е₃ задана гладкая кривая L.

 

Пусть на кривой L задана скалярная функция f (x,y,z).

Замечание: Если t₁, t₂ такие, что x(t₁) = x(t₂), y(t₁) = y(t₂), z(t₁) = z(t₂), то кривая L имеет самопересечение, но, при этом f (x(t₁), y(t₁), z(t₁)) не обязательно совпадает с f (x(t₂), y(t₂), z(t₂)), поэтому, записывая f (x,y,z) мы будем иметь в виду f (x(t), y(t), z(t)).

 

Рассмотрим промежуток [a,b] изменения параметра t , и на [a,b] зададим разбиение P с отмеченными точками ξ, т.е. зададим (P,ξ).

Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривой L с отмеченными точками.

 

Рассмотрим: , где 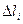– длина хорды, соединяющей концы соответствующего участка кривой. Если такой предел существует и конечен, то он называется криволинейным интегралом 1^го рода , и обозначается .

Физический смысл криволинейного интеграла 1^го рода – масса кривой L с линейной плотностью масс f (x, y, z).

Для нахождения элемента длины дуги будут полезны следующие формулы:

1⁰. Для плоской кривой, заданной в декартовых координатах:

dl = (по теореме Пифагора, см. рис. а).

В частных случаях различных способов задания кривой L получаем:

1а. Если y = y(x), то dl = ;

1б. Если x = x(y), то dl = ;

1в. Если x = x(t), y = y(t), то dl = ;

2⁰. Для плоской кривой, заданной в полярных координатах x = ρcosφ, y = ρsinφ:

dl = . Формула эта может быть получена и непосредственно из криволинейного треугольника (см. рис. б).

2а. Если , то dl = ;

2б. Если , то dl = ;

2в. Если , то dl = ;

3⁰. Для пространственной кривой, заданной в декартовых координатах:

dl = .

3а. Если , то dl = ;

 

4⁰. Если f (x, y, z) = 1 то криволинейный интеграл 1^го рода численно равен длине кривой и кривая называется спрямляемой.

5⁰. Криволинейный интеграл 1^го рода может быть сведен к обычному интегралу Римана. Пусть . Тогда

. При этом .

Формула следует из определения.

 

4⁰. Криволинейный интеграл 1^го рода не зависит от направления интегрирования:

.

 

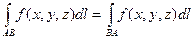Примеры:

1⁰.Вычислить: J= , где кривая L: .

Параметрическое уравнение эллипса: Þ

dl = .

Эллипс пробегается противчасовой стрелки, хотя это указывать не обязательно.

И тогда:

J = = =

= .

 

2⁰.Найти массу кривой L : y = ln x для , если ρ = x² линейная плотность кривой .

M = =

= = .

3⁰.Найти силу притяжения точки А массы mоднородной полуокружностью радиуса Rс центром в точке А. ( ).

Отметим, что сила притяжения это вектор , который из соображений симметрии направлен вверх. Найдем F_y (т.к. F_x = 0).

dF_y = , где G – гравитационная постоянная, dl = R dφ; Следовательно: F_y = .

 

§. Криволинейные интегралы 2^го рода.

Def : Пусть в Е₃ задана вектор-функция , и при этом x(t), y(t), z(t) C_[a,b], C¹_[a,b] , т.е. в Е₃ задана гладкая кривая L.

Пусть на кривой L задана векторная функция:

.

Рассмотрим промежуток [a,b] изменения параметра t , и на [a,b] зададим разбиение P с отмеченными точками ξ, т.е. зададим (P,ξ). Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривой L с отмеченными точками. И рассмотрим:

.

Если такой предел существует, то он называется криволинейным интегралом 2^го рода и обозначается: .

 

Геометрический смысл криволинейного интеграла 2^го рода – работа силового поля 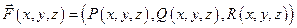вдоль кривой L.

 

1⁰.Если , и при этом x(t), y(t), z(t) C_[a,b], C¹_[a,b] ,

=

= .

 

Эта формула дает способ вычисления криволинейного интеграла 2^го рода сведением к интегралу Римана, и следует из определения, в котором в левой части фактически записана интегральная сумма для интеграла стоящего в правой части.

 

2⁰.Формула для вычисления криволинейного интеграла 2^-го рода:

.

Здесь – единичный вектор касательной к кривой, а – его направляющие косинусы.

3⁰. .

4⁰. Формула Грина. Пусть G – плоская область и γ – кусочногладкий контур, являющийся границей области G. Пусть в заданы P(x,y) и Q(x,y), непрерывные в G вместе с и . Тогда: .

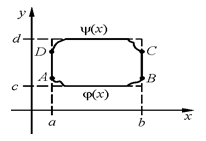Замечание: γ⁺ - означает, что контур γ проходится в положительном направлении – т.е. против часовой стрелки (при обходе контура левая рука все время находится в области.

 

Δ. Рассмотрим: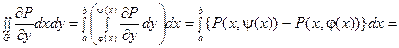

= .

Здесь учтено, что интегралы и равны нулю из-за того, что на промежутках BC и DA .

Таким образом: = . Аналогично: = .

После сложения двух полученных формул, получаем доказываемую формулу. ▲

 

Примеры :

1⁰. Вычислить , если кривая L соединяет точки от (0,0) до (1,1).

a. y = x ; б. y = x²; в. x = y² .

а). J = .

б). J = .

в). J = .

Выясняется, что интегралы получаются разные, т.е. значение интеграла зависит не только от начальной и конечной точек кривой, но и от самой кривой L.

2⁰. Вычислить вдоль тех же кривых, что и в предыдущей задаче.

a) J = . б) J = .

в) J = .

а в данной задаче на всех трех исследованных путях результат один и тот же. Это не означает, что и на других путях так будет, но…

г) Рассмотрим J = .

Проведенная выкладка показывает, что интеграл действительно не зависит от пути интегрирования (здесь нет никакого конкретного пути), а зависит только от начальной и конечной точки дуги.

Когда же будет наблюдаться такое явление?

 

§. Условия независимости криволинейного интеграла 2^го рода