 |
|
От пути интегрирования.
Т0. Пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) определены и непрерывны в
области G , лежащей на гладкой поверхности S, и γ – граница области G.
Тогда эквивалентны следующие условия:
A*). Для любого замкнутого контура γ в G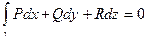 
;
B*). Для любых A,B є G 
не зависит от кривой, соединяющей
точки A и B, и лежащей в области G;
С*). Выражение Pdx + Qdy + Rdz в G является полным дифференциалом
некоторой функции U(x, y, z), т.е. 
U = U(x, y, z) такая,что dU = Pdx+Qdy+Rdz;
D*). Для функций P(x, y, z), Q(x, y, z), R(x, y, z) в области G выполняются условия:
; 
; 
.
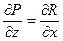При этом :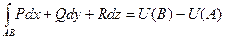 
(*)
Последнюю формулу можно назвать формулой Ньютона-Лейбница для криволинейных интегралов.
Замечание 1. (связь А* и В*).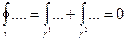 
не зависит от кривой L, соединяющей точки А и В.
Замечание 2. (связь С* и D*).
Если U(x, y, z) такая, что 
,
то 
, 
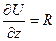Þ 
;
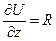
Þ 
; 
Þ 
.
Замечание 3. В случае независимости криволинейного интеграла от пути
интегрирования, U(x, y, z) такая что:
.
Физикиназывают функцию U(x, y, z) потенциалом векторного поля 
, а поле F – потенциальным – “ Работа равна разности потенциалов”.
Математики называют функцию U(x, y, z) первообразной для Pdx+Qdy+Rdz –
интеграл равен разности первообразных в конце и начале пути.
Примеры:
10.Вычислить 
для различных контуров γ.
а). Пусть контур γ ограничивающий область G таков, что 
не содержит т. (0,0). Для вычисления интеграла воспользуемся формулой Грина.
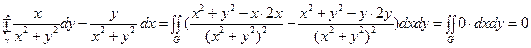где,
, 
, 
, 
.
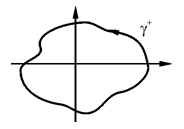
б). Пусть контур γ+ окружает точку (0,0). В этом случае нельзя применить формулу Грина ибо 
и 
в точке (0,0) не существуют.
Отметим, что все интегралы по таким контурам совпадают между собой.
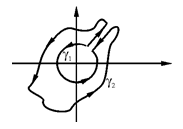Иллюстрация : 
Þ
Þ 
.
в). Тогда достаточно вычислить скажем, по окружности 
. 
.
г). Легко видеть, что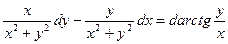 
.
Следовательно, 
, если контур не проходит через точку (0,0) т.к. начальная и конечная точки замкнутого контура совпадают.
20. Найти первообразную, если:
.
Проверка показывает, что условия ; ; 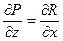выполняются.
Таким образом, задача о нахождении первообразной поставлена корректно. Тогда,
1). 
и интегрирование по 
дает: 
.
Отсюда 
. Но 
из условия задачи.
2). Тогда 
Þ 
.
Интегрирование по 
дает 
.
Значит: 
.
Отсюда 
. Но из условия задачи 
.
3) Тогда 
Þ 
.
Итог: 
. Первообразная найдена с точностью до произвольного постоянного слагаемого. Большего и желать не приходится.