 |
|
Примеры решения задач
ЗАДАЧА 1. Два точечных заряда  Кл и q2 = 1,5×10-8 Кл расположены на расстоянии r12 = 10 cм друг от друга. Найти силу, действующую на точечный заряд q = 10-9 Кл, помещенный на продолжение прямой r12 на расстоянии r23 = 2 см от заряда q2 (рис. 2.1.1).
Кл и q2 = 1,5×10-8 Кл расположены на расстоянии r12 = 10 cм друг от друга. Найти силу, действующую на точечный заряд q = 10-9 Кл, помещенный на продолжение прямой r12 на расстоянии r23 = 2 см от заряда q2 (рис. 2.1.1).
ДАНО:
 Кл Кл
 Кл Кл
 Кл Кл
 м м
 м м
|
| F – ? |
АНАЛИЗ. В задаче рассматривается взаимодействие точечных зарядов, поэтому для определения силы воспользуемся законом Кулона. Сила  , действующая на заряд q, складывается из сил, действующих на него со стороны полей первого и второго зарядов:
, действующая на заряд q, складывается из сил, действующих на него со стороны полей первого и второго зарядов:  .
.
 Рис. 2.1.1
Рис. 2.1.1
|
РЕШЕНИЕ. Направим ось ОХ по прямой, соединяющей заряды. Силы  и
и  являются центральными, они направлены по прямой, соединяющей заряды. Поэтому можно перейти к скалярному равенству:
являются центральными, они направлены по прямой, соединяющей заряды. Поэтому можно перейти к скалярному равенству:
F = F2 – F1 .
Этот переход совершен с учётом знаков зарядов. Величины сил F1 и F2 определяются по закону Кулона:

Таким образом,



Проверим размерность:
 . Подставим значения:
. Подставим значения:

ОТВЕТ: 
ЗАДАЧА 2. Найти силу, действующую на точечный заряд q = 10-9 Кл, расположенный в центре полукольца радиусом r0 = 5 см, со стороны этого полукольца, по которому равномерно распределён заряд Q = 3×10–7 Кл.
ДАНО:
 Кл Кл
 м м
 Кл Кл
|
| F – ? |
АНАЛИЗ. В задаче исследуется электростатическое взаимодействие равномерно заряженного полукольца и точечного заряда. Полукольцо нельзя рассматривать как точечный заряд, поэтому воспользоваться непосредственно законом Кулона невозможно. Однако этот закон можно применить, если рассматривать силу  , действующую на заряд q, со стороны достаточно малых равных элементов полукольца d
, действующую на заряд q, со стороны достаточно малых равных элементов полукольца d 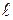 , на которые его можно разбить. Если заряд Q распределён по полукольцу равномерно, то заряд элемента d
, на которые его можно разбить. Если заряд Q распределён по полукольцу равномерно, то заряд элемента d 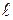 можно считать точечным и равным
можно считать точечным и равным  . Элементарная сила
. Элементарная сила  , действующая на точечный заряд q, направлена по прямой, соединяющей заряд q и заряд dQ (рис. 2.1.2). Модуль элементарной силы
, действующая на точечный заряд q, направлена по прямой, соединяющей заряд q и заряд dQ (рис. 2.1.2). Модуль элементарной силы  согласно закону Кулона равен:
согласно закону Кулона равен:

 Рис. 2.1.2
Рис. 2.1.2
|
Сила, действующая на заряд q со стороны полукольца, определяется как векторная сумма элементарных сил  :
:  – заряд распределён по полукольцу непрерывно, и операция суммирования переходит в операцию интегрирования.
– заряд распределён по полукольцу непрерывно, и операция суммирования переходит в операцию интегрирования.
При переходе от одного элемента к другому модуль элементарных сил изменяться не будет, а будет меняться лишь направление.
РЕШЕНИЕ. Поместим начало координат в точку, где расположен заряд q, тогда проекции элементарных сил на координатные оси зависят от переменного угла 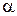 :
:
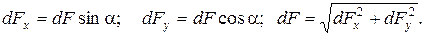
Чтобы найти проекции результирующей силы  на оси, проинтегрируем соответствующие проекции элементарных сил по полукольцу:
на оси, проинтегрируем соответствующие проекции элементарных сил по полукольцу:

Интеграл берется по полукольцу, что соответствует изменению угла от 0 до π.
Учитывая, что  получим:
получим:

Проверим размерность:  . Подставим значения:
. Подставим значения:  мН.
мН.
Направление силы  по оси ОХ и равенство нулю её проекции на ось ОY можно предсказать из соображений симметрии.
по оси ОХ и равенство нулю её проекции на ось ОY можно предсказать из соображений симметрии.
ОТВЕТ:  мН.
мН.
ЗАДАЧА 3. По тонкой нити длиной 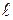 0 равномерно распределён заряд Q линейной плотностью τ. Найти напряженность поля в точке А, расположенной на расстоянии а от нити. Положение точки А определяется углами
0 равномерно распределён заряд Q линейной плотностью τ. Найти напряженность поля в точке А, расположенной на расстоянии а от нити. Положение точки А определяется углами  и
и  (рис. 2.1.3).
(рис. 2.1.3).
ДАНО:
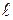 0 ,м
Q ,Кл
τ,Кл/м
а, м 0 ,м
Q ,Кл
τ,Кл/м
а, м
 ; ; 
|
| Е – ? |
АНАЛИЗ. Электростатическое поле образовано равномерно заряженной нитью. Для определения напряженности этого поля воспользуемся принципом суперпозиции электрических полей. На основании закона Кулона можно найти напряженность поля, созданного точечным зарядом. Разобьём нить на бесконечно малые элементы длиной  . Каждый такой элемент обладает зарядом
. Каждый такой элемент обладает зарядом  , который можно считать точечным. Модуль напряженности электрического поля, созданного зарядом, определяется по формуле
, который можно считать точечным. Модуль напряженности электрического поля, созданного зарядом, определяется по формуле
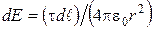 , (2.1.1)
, (2.1.1)
где r – расстояние от элемента  до точки А.
до точки А.
Элементарный вектор  направлен по прямой, соединяющей элемент
направлен по прямой, соединяющей элемент  и точку А, под углом
и точку А, под углом 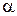 к оси Х. Результирующий вектор
к оси Х. Результирующий вектор  получим, суммируя элементарные векторы
получим, суммируя элементарные векторы  от всех элементов нити
от всех элементов нити

РЕШЕНИЕ. Спроектируем последнее равенство на координатные оси (рис. 2.1.3), при этом модуль вектора напряженности равен  ,
,

Из рис. 2.1.3 видно, что
 (2.1.2)
(2.1.2)
 Рис. 2.1.3
Рис. 2.1.3
|
При интегрировании по нити будут меняться значения 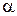 и r, поэтому все переменные следует выразить через одну – угол
и r, поэтому все переменные следует выразить через одну – угол 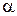 :
:
 (2.1.3)
(2.1.3)
Координата у элемента нити  равна
равна 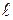 :
: 
 тогда
тогда
 . (2.1.4)
. (2.1.4)
Подставляя в (2.1.1) выражения (2.1.3) и (2.1.4), получим  .
.
Согласно равенствам (2.1.2),


или окончательно

Проверим размерность:  .
.
Рассмотрим частные случаи, вытекающие из полученных формул:
1. Точка А расположена на перпендикуляре, проведённом через середину нити, 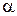 1 =
1 = 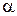 2 =
2 = 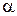 , тогда
, тогда

2. Точка А расположена на перпендикуляре, проведённом к нити через один из её концов, 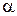 1 = 0 ,
1 = 0 , 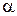 2 =
2 = 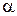 , тогда
, тогда

3. Бесконечная нить, 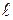 >>a,
>>a,  стремиться к
стремиться к 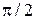 ,
,  стремиться к –
стремиться к – 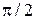 , тогда
, тогда  В этом случае силовые линии лежат в плоскостях, перпендикулярных заряженной нити и лучами расходятся от неё. При приближении исследуемой точки А к концам нити будет появляться составляющая
В этом случае силовые линии лежат в плоскостях, перпендикулярных заряженной нити и лучами расходятся от неё. При приближении исследуемой точки А к концам нити будет появляться составляющая
Eу , плоскорадиальная симметрия нарушается.
ОТВЕТ: 
ЗАДАЧА 4. В вакууме образовалось скопление зарядов в форме тонкого длинного цилиндра с постоянной объёмной плотностью ρ. Найти напряженность поля в точках, лежащих внутри и вне цилиндра.
| ДАНО: ρ, Кл/м3 R, м |
| Е – ? |
АНАЛИЗ. Электростатическое поле образовано бесконечно длинным равномерно заряженным цилиндром. Симметричное распределение зарядов позволяет для нахождения вектора  применять теорему Гаусса. Длина цилиндра
применять теорему Гаусса. Длина цилиндра 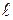 много больше его радиуса R (цилиндр бесконечно длинный), поэтому в средней части цилиндра силовые линии располагаются радиально, а поле обладает плоскорадиальной симметрией (рис. 2.1.4). Вспомогательной Гауссовой поверхности придадим форму цилиндрической, коаксиальной с заряженным цилиндром. Точка, в которой определяется поле, лежит на боковой поверхности вспомогательного цилиндра на расстоянии rА от оси цилиндра. Длина вспомогательной цилиндрической поверхности h произвольна, но много меньше длины самого цилиндра, h <<
много больше его радиуса R (цилиндр бесконечно длинный), поэтому в средней части цилиндра силовые линии располагаются радиально, а поле обладает плоскорадиальной симметрией (рис. 2.1.4). Вспомогательной Гауссовой поверхности придадим форму цилиндрической, коаксиальной с заряженным цилиндром. Точка, в которой определяется поле, лежит на боковой поверхности вспомогательного цилиндра на расстоянии rА от оси цилиндра. Длина вспомогательной цилиндрической поверхности h произвольна, но много меньше длины самого цилиндра, h << 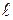 .
.
РЕШЕНИЕ. Решим задачу для случая r > R. По теореме Гаусса для поля в вакууме
 (2.1.5)
(2.1.5)
 Рис. 2.1.4
Рис. 2.1.4
|
Поток вектора напряженности через замкнутую цилиндрическую поверхность складывается из потоков через боковую поверхность и через основания вспомогательного цилиндра, поэтому интеграл в равенстве (2.1.5) следует разбить на три интеграла: по боковой поверхности Sбок, верхнему и нижнему основаниям S1, S2

Поскольку нормаль к основаниям цилиндра составляет угол 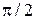 с вектором
с вектором  , то
, то

На поверхности Sбок угол  , и
, и 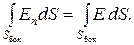
Боковая поверхность вспомогательного цилиндра симметрична относительно заряда, поэтому E = 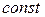 на всей поверхности Sбок и
на всей поверхности Sбок и  Очевидно,
Очевидно,  в результате получим
в результате получим
 (2.1.6)
(2.1.6)
Внутри поверхности интегрирования находится заряд, вырезаемый поверхностью  из заряженного цилиндра. По условию задачи ρ =
из заряженного цилиндра. По условию задачи ρ = 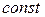 , поэтому
, поэтому
 . (2.1.7)
. (2.1.7)
Подставим выражения (2.1.6) и (2.1.7) в равенство (2.1.5): 
 (2.1.8)
(2.1.8)
Произведение  представляет заряд, приходящийся на единицу длины заряженного цилиндра, т. е. линейную плотность заряда. Следовательно, формуле (2.1.8) можно придать вид:
представляет заряд, приходящийся на единицу длины заряженного цилиндра, т. е. линейную плотность заряда. Следовательно, формуле (2.1.8) можно придать вид:

Проверим размерность:  .
.
Найдём напряженность поля в точках, лежащих внутри цилиндра, при r < R. Вспомогательную поверхность  выбираем в виде цилиндра радиусом rВ и высотой h (rВ< R). По теореме Гаусса
выбираем в виде цилиндра радиусом rВ и высотой h (rВ< R). По теореме Гаусса
 (2.1.9)
(2.1.9)
Внутри поверхности интегрирования находится заряд, вырезаемый поверхностью S  из заряженного цилиндра и равный
из заряженного цилиндра и равный

 . (2.1.10)
. (2.1.10)
При вычислении потока вектора напряженности через поверхность SВ следует повторить все рассуждения, которые были проведены для поверхности SA , тогда
 (2.1.11)
(2.1.11)
Подставим (2.1.10) и (2.1.11) в (2.1.9):  и
и  где r
где r  – текущий радиус.
– текущий радиус.
Проверим размерность выражения:  .
.
График зависимости E (r) представлен на рис. 2.1.5. Для r = R,ER =  .
.

Рис. 2.1.5
ОТВЕТ:  при r > R;
при r > R; 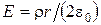 при r < R.
при r < R.
ЗАДАЧА 5. Электрическое поле создано тонкой бесконечно длиной нитью, равномерно заряженной с линейной плотностью τ= 30 нКл/м. На расстоянии а = 20 см от нити находится плоская круглая площадка радиусом r = 1 см. Определить поток вектора напряженности через эту площадку, если плоскость её составляет угол β = 30° с линией напряженности, проходящей через середину площадки (рис. 2.1.6).
| ДАНО: τ = 30×10–9 Кл/м а = 0,20 м r = 0,01 м β = 30° |
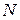 – ? – ?
|
АНАЛИЗ. Электростатическое поле, создаваемое бесконечной заряженной нитью, не является однородным – линии вектора напряженности радиально расходятся от нити, поэтому во всех точках площадки значения и направления вектора  различны. В этом случае поток вектора напряженности через площадку равен интегралу
различны. В этом случае поток вектора напряженности через площадку равен интегралу  где En – проекция вектора
где En – проекция вектора  на нормаль
на нормаль  к поверхности площадки dS,
к поверхности площадки dS, 
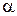 – угол между направлением
– угол между направлением  и нормалью
и нормалью  . Тогда
. Тогда
 .
.
 Рис. 2.1.6
Рис. 2.1.6
|
РЕШЕНИЕ. Размеры площадки малы, r << a, поэтому электрическое поле в пределах площадки можно считать однородным и равным полю в центре площадки:  В этом случае
В этом случае  Тогда
Тогда
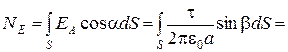

Проверим размерность:
 . Подставим значения
. Подставим значения 
ОТВЕТ: 
ЗАДАЧА 6. Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут заряды q1 = 1 нКл и q2 = – 0,5 нКл. Найти напряженность E поля в точках, отстоящих от центра сфер на расстояние r1 = 5 см , r2 = 9 см и r3 = 15 см. Построить график зависимости E(r).
| ДАНО: R1 = 0,06 м R2 = 10 м q1 = 1×10–9 Кл q2 = – 0,5×10–9 Кл r1 = 0,05 м r2 = 0,09 м r2 = 0,09 м |
| Е – ? |
АНАЛИЗ. Точки, в которых нужно найти напряженность, лежат в трёх областях (рис. 2.1.7): область I (r1< R1); область II (R1< r2 <R2); область III (r3 >R2). Симметричное распределение зарядов позволяет для решения задачи применить теорему Гаусса.
 Рис. 2.1.7
Рис. 2.1.7
|
РЕШЕНИЕ. 1. Найдем напряженность электростатического поля в области I. Для этого проведём вспомогательную сферическую поверхность S1 радиусом r1. Внутри этой поверхности зарядов нет, поэтому по теореме Гаусса

Из соображений симметрии
E1 = E1n = 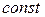 ,
,
следовательно,  Очевидно,
Очевидно,  , поэтому E1 = 0 – напряженность поля во всех точках, удовлетворяющих условию r < R1 , равна нулю.
, поэтому E1 = 0 – напряженность поля во всех точках, удовлетворяющих условию r < R1 , равна нулю.
2. Определим напряженность E2 в области II. Построим вспомогательную сферическую поверхность радиусом r2. По теореме Гаусса  . Из условий симметрии E2 = En =
. Из условий симметрии E2 = En = 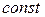 , тогда
, тогда  Ясно, что
Ясно, что
 поэтому
поэтому 
Проверим размерность этого выражения:
 .
.
Подставим значения: 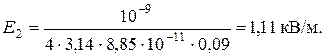
3. Вычислим напряженность поля в области III. Проведём вспомогательную сферическую поверхность радиусом r3 . Эта поверхность охватывает зарядq1 + q2 , следовательно, по теореме Гаусса  Учитывая, что E3 = En =
Учитывая, что E3 = En = 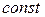 и
и  получим:
получим: 
Правильность формулы по размерности очевидна. Подставим значения:

Построим график зависимости E = E(r). При r < R1 (область I) E1 = 0.
В области II 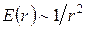 , в точке А
, в точке А  ,
,  В/м, в точке В r = R2,
В/м, в точке В r = R2,  В/м – слева.
В/м – слева.
В области III  , причем при
, причем при  справа
справа  В/м, т. е. в точке
В/м, т. е. в точке  функция E(r) терпит разрыв. График функции E = E(r) представлен на рис. 2.1.8.
функция E(r) терпит разрыв. График функции E = E(r) представлен на рис. 2.1.8.

Рис. 2.1.8
ОТВЕТ: E1 = 0; 

ЗАДАЧА 7. 
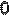 Заряд Q равномерно распределен по кольцу радиусом R. Найти потенциал относительно бесконечности и напряженность на оси кольца как функцию расстояния h от центра кольца. Построить графики зависимостей E(h) и j(h).
Заряд Q равномерно распределен по кольцу радиусом R. Найти потенциал относительно бесконечности и напряженность на оси кольца как функцию расстояния h от центра кольца. Построить графики зависимостей E(h) и j(h).
| ДАНО: Q, Кл R, м |
| E (h) – ? j(h) – ? |
АНАЛИЗ. Электростатическое поле создано равномерно заряженным кольцом, которое нельзя считать точечным зарядом. Для определения потенциала этого поля воспользуемся принципом суперпозиции электрических полей, разбив кольцо на элементарные заряды и определив потенциал поля каждого такого точечного заряда. Суммарный потенциал, очевидно, равен сумме этих потенциалов. При непрерывном распределении зарядов операция суммирования переходит в операцию интегрирования:
 Рис. 2.1.9
Рис. 2.1.9
|

Для определения напряженности поля следует воспользоваться связью напряженности и потенциала

РЕШЕНИЕ. Разобьём кольцо на элементарные заряды  (рис. 2.1.9).
(рис. 2.1.9).
Потенциал поля, создаваемый каждым элементарным зарядом  в точке А, лежащей на расстоянии h от центра кольца, равен
в точке А, лежащей на расстоянии h от центра кольца, равен 
Из рис. 2.1.9 видно, что  Заряд элемента d
Заряд элемента d 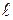 кольца равен
кольца равен  . Тогда
. Тогда

Проверим размерность:  .
.
Связь напряженности и потенциала дает:  ;
;
 ;
; 
Проверим размерность:  .
.
Построим зависимость j(h) (рис. 2.1.10). При h = 0 (в центре кольца)  , при
, при 
 .
.
График симметричен относительно оси j. При 
 . Для j(h) это точка перегиба. Зависимость E(h) представлена на рис.2.1.11. При h = 0 E = 0;
. Для j(h) это точка перегиба. Зависимость E(h) представлена на рис.2.1.11. При h = 0 E = 0;  –экстремумы функции E(h).
–экстремумы функции E(h).


Рис. 2.1.10 Рис. 2.1.11
ОТВЕТ: 

ЗАДАЧА 8. Электрическое поле образовано положительно заряженной бесконечной нитью с линейной плотностью заряда τ = 2×10-9 Кл/см. Какую скорость получит электрон под действием этого поля, приблизившись к нити с расстояния r1 = 1 см до расстояния r2 = 0,5 см.
| ДАНО: τ = 2×10-11 Кл/м r1 = 0,01 м r2 = 0,005 м |
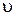 – ? – ?
|
АНАЛИЗ. Электростатическое поле образовано заряженной нитью. Зависимость напряженности этого поля от расстояния до нити можно считать известной (см. задачу 3). Потенциальное электрическое поле совершает работу по перемещению электрона с зарядом –е. В результате потенциальная энергия поля WP убывает. Она переходит в кинетическую энергию электрона WK , причем ∆WK = – ∆WP , где ∆WK – приращение кинетической энергии электрона. Очевидно, убыль потенциальной энергии 
Разность потенциалов найдем, пользуясь связью напряженности и потенциала.
РЕШЕНИЕ. Приращение кинетической энергии равно  причем
причем  поэтому
поэтому  Очевидно, скорость электрона равна
Очевидно, скорость электрона равна
 . (2.1.12)
. (2.1.12)
Для нахождения разности потенциалов в неоднородном поле, создаваемом положительно заряженной нитью, воспользуемся выражением для напряжённости поля нити
 (2.1.13)
(2.1.13)
и связью напряженности и потенциала  . Заряд движется вдоль силовой линии, поэтому
. Заряд движется вдоль силовой линии, поэтому 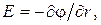 и
и 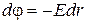 . Проинтегрировав, получаем
. Проинтегрировав, получаем
 .
.
Подставляя значение E из (2.1.13) получим
 .
.
Найденные значения разности потенциалов подставим в формулу (2.1.12):

Проверим размерность:
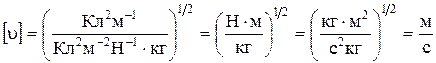 , подставим значения
, подставим значения

ОТВЕТ: 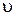 = 2,97×107 м/с.
= 2,97×107 м/с.
ЗАДАЧА 9. Показать, что векторное поле  потенциально. Найти, как распределен заряд, создающий поле в этой области.
потенциально. Найти, как распределен заряд, создающий поле в этой области.
ДАНО:

|

|
АНАЛИЗ. Поле является потенциальным, если rot  = 0. Для определения распределения заряда следует воспользоваться дифференциальной формой теоремы Гаусса
= 0. Для определения распределения заряда следует воспользоваться дифференциальной формой теоремы Гаусса  .
.
РЕШЕНИЕ. Найдем ротор вектора  :
:

Подставив значения  получим:
получим:

Следовательно,  – рассматриваемое поле потенциально.
– рассматриваемое поле потенциально.
Объёмную плотность заряда ρ найдем из теоремы Гаусса 
Для данного поля в исследуемой области  тогда
тогда

– поле представляет собой потенциальное электрическое поле в области, свободной от зарядов.
Правильность формулы по размерности очевидна.
ОТВЕТ: 
ЗАДАЧА 10. Задано двумерное электрическое поле, напряженность которого определяется формулами: E = ρ0a2/ 2ε0 в области I, где r > a, E = ρ0r / 2ε0 в области II, где r < a,при ρ0 = 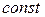 в каждой из областей. Найти объёмную плотность заряда в областях I и II. Показать, что поле потенциально. Привести конкретный пример распределения заряда, создающего такое поле.
в каждой из областей. Найти объёмную плотность заряда в областях I и II. Показать, что поле потенциально. Привести конкретный пример распределения заряда, создающего такое поле.
| ДАНО: E = r0a2 /2ε0 при r > a E = r0r /2ε0 при где r < a;ρ0= сonst |
| r–? |
АНАЛИЗ. Для определения объемной плотности заряда следует воспользоваться дифференциальной формой теоремы Гаусса.
Чтобы показать потенциальный характер поля, необходимо найти rot  и убедиться, что он равен нулю.
и убедиться, что он равен нулю.
РЕШЕНИЕ. Из теоремы Гаусса следует, что
 .
.
Задача сводится к нахождению дивергенции поля в областях I и II. В прямоугольной системе координат 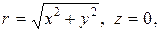 т. к. поле двумерно.
т. к. поле двумерно.
Проекции вектора  на оси X,Y,Z в области I, где r > a, соответственно равны:
на оси X,Y,Z в области I, где r > a, соответственно равны:

В области II, где r < a ,

Для области I



Таким образом, в области I дивергенция  и объёмная плотность заряда r = 0 (область свободна от зарядов).
и объёмная плотность заряда r = 0 (область свободна от зарядов).
Для области II

Следовательно, r = r0. Правильность формулы по размерности очевидна. В области II  плотность заряда ρпостоянна и определяется величиной r0.
плотность заряда ρпостоянна и определяется величиной r0.
Исследуемое поле потенциально, т. к. ротор его и в области I и в области II равен нулю:
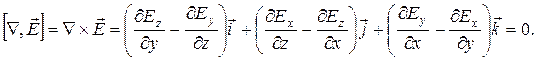
Подобное поле легко представить. Это поле, создаваемое бесконечно длинным круговым цилиндром радиусом а, заполненным положительным зарядом, распределенным с объемной плотностью r0. Ось симметрии совпадает с осью Z .
Заряд за пределами цилиндра отсутствует, внутри цилиндра во всех точках он постоянен и равен ρ0.
ОТВЕТ: При r > a r = 0;при r < a r = r0 .
ЗАДАЧА 11. Потенциал поля в некоторой области пространства зависит только от координаты x: 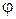 = ах3+b, где а (В/м3), b (В) – некоторые постоянные. Найти распределение объемного заряда ρ(х).
= ах3+b, где а (В/м3), b (В) – некоторые постоянные. Найти распределение объемного заряда ρ(х).
ДАНО:
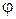 = ах3 + b
а,В/м3
b,В = ах3 + b
а,В/м3
b,В
|
 (х) – ? (х) – ?
|
АНАЛИЗ. Связь объемной плотности заряда с потенциалом дает уравнение Пуассона  .
.
РЕШЕНИЕ. Функция 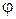 зависит только от переменной х, поэтому
зависит только от переменной х, поэтому
 . Тогда
. Тогда  , и
, и  , или
, или 
Проверим размерность:  .
.
ОТВЕТ: 
ЗАДАЧА 12. Три точечных заряда q1, q2, q3 образуют электрически нейтральную систему, причём q1 = q2 = 10 нКл. Заряды расположены в вершинах равностороннего треугольника. Определить максимальные значения напряженности Emaxи потенциала  поля, создаваемого этой системой зарядов на расстоянии r = 1 м от центра треугольника, если длина стороны а = 10 см.
поля, создаваемого этой системой зарядов на расстоянии r = 1 м от центра треугольника, если длина стороны а = 10 см.
| ДАНО: r = 1 м а = 0,10 м q1 = q2 = 10×10–9 Кл q1+q2+q3 = 0 |
Emax– ?
 – ? – ?
|
АНАЛИЗ. Нейтральную систему, состоящую из трех точечных зарядов, можно представить в виде диполя (рис.2.1.12 а). Действительно, «центр тяжести» зарядов q1 и q2лежит на середине отрезка прямой, соединяющей эти заряды (точка В на рис. 2.1.12 а), и можно считать, что в точке В находится заряд q = q1 + q2. Из условия нейтральности системы зарядов имеем: q1 + q2 + q3= 0,
 или q3 = – (q1 + q2) = – q.
или q3 = – (q1 + q2) = – q.

а) б)
Рис. 2.1.12
Расстояние 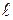 между зарядами q3 и –q много меньше r (
между зарядами q3 и –q много меньше r ( 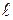 << r), следовательно, систему этих двух зарядов можно считать электрическим диполем, (рис. 2.1.12 б), дипольный момент которого
<< r), следовательно, систему этих двух зарядов можно считать электрическим диполем, (рис. 2.1.12 б), дипольный момент которого 
 , где
, где  – плечо диполя.
– плечо диполя.
Напряженность поля диполя выражается формулой 
где 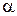 – угол между векторами
– угол между векторами  и
и  (рис. 2.1.12б).
(рис. 2.1.12б).
Потенциал поля диполя равен  . Очевидно, максимальные значения напряженности и потенциала достигаются при
. Очевидно, максимальные значения напряженности и потенциала достигаются при 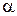 = 0.
= 0.
РЕШЕНИЕ. Из рис. 2.1.12 а видно, что модуль плеча диполя (q3; –q)равен  тогда
тогда

Тот же результат можно получить, если систему из трех зарядов представить двумя диполями с электрическими моментами  и
и  , (рис. 2.1.13), причем их модули соответственно равны р1 = q1 a; р2 = q2 a.
, (рис. 2.1.13), причем их модули соответственно равны р1 = q1 a; р2 = q2 a.
 Электрический момент
Электрический момент  системы зарядов равен векторной сумме
системы зарядов равен векторной сумме  Из рис. 2.1.13 видно, что
Из рис. 2.1.13 видно, что  , и
, и  ,
,
тогда  – результат совпадает с найденным ранее значением.
– результат совпадает с найденным ранее значением.
Напряженность будет иметь максимальное значение при 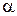 = 0, поэтому
= 0, поэтому
 .
.
Проверим размерность  .
.
Подставим значения 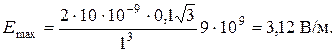
Потенциал поля диполя максимален при 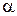 = 0,
= 0,

Проверим размерность: 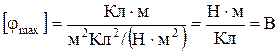 . Подставим значения
. Подставим значения 
ОТВЕТ: 

ЗАДАЧА 13. Диполь с электрическим моментом р = 2 нКл×м находится в однородном электрическом поле напряженностью E = 30 кВ/м. Вектор  составляет угол a0= 60° с направлением силовых линий поля. Определить произведённую внешними силами работу А поворота диполя на угол β = 30°.
составляет угол a0= 60° с направлением силовых линий поля. Определить произведённую внешними силами работу А поворота диполя на угол β = 30°.
| ДАНО: р = 2×10–9 Кл×м E = 30×103 В/м a0= 60° β = 30° |
| А – ? |
АНАЛИЗ. Из исходного положения (рис. 2.1.14 а) диполь можно повернуть на угол β = 30° =  двумя способами:
двумя способами:
– по часовой стрелке до угла a1 = a0 – β =  (рис. 2.1.14 б);
(рис. 2.1.14 б);
– против часовой стрелки до угла a2 = a0 + β = 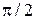 (рис.2.1.14в).
(рис.2.1.14в).
В первом случае диполь будет поворачиваться под действием сил поля, и работа внешних сил отрицательна. Во втором случае поворот может быть произведен только действием внешних сил, работа внешних сил положительна.
РЕШЕНИЕ. Работу, совершаемую при повороте диполя, можно вычислить двумя способами.



а) б) в)
Рис. 2.1.14
1 способ. Элементарная работа при повороте диполя на угол daравна 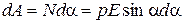 где N – момент внешних сил. Полная работа при повороте диполя на угол (a – a0) равна
где N – момент внешних сил. Полная работа при повороте диполя на угол (a – a0) равна
 .
.
Правильность формулы по размерности очевидна.
При повороте диполя по часовой стрелке  , подставив значения, получаем
, подставив значения, получаем 
Против часовой стрелки  Подставим значения
Подставим значения

2 способ. Работа совершается внешними силами за счет уменьшения потенциальной энергии диполя  .
.
Потенциальная энергия диполя в электрическом поле в начальном и конечном состояниях равна: 
Тогда работа  – мы пришли к той же формуле, что и в первом способе.
– мы пришли к той же формуле, что и в первом способе.
ОТВЕТ:  мкДж,
мкДж,  мкДж.
мкДж.