Главная | Обратная связь

Задача использования ресурсов

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Контрольные работы и методические указания для студентов заочного отделения

 

Введение

При решении практических задач в экономике, производственном менеджменте часто возникает необходимость нахождения максимальной прибыли, минимальных затрат при выполнении некоторых экономических, природных и т. п. ограничений. С математической точки зрения, вышесказанное может означать необходимость нахождения максимума или минимума некоторой функции многих переменных:

, (1)

когда на эти переменные накладываются некоторые ограничения вида:

(2)

Задачи подобного рода называются задачами математического программирования. Функция (1) называется целевой функцией. Функции f и – есть некоторые заданные функции. В формуле (2) 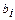есть заданные константы.

Существует множество разделов математического программирования, которые решают свой класс задач, зависящий от типа функций (1) и (2).

Если целевая функция (1) и все функции в (2) являются линейными, то задача (1), (2) решается методами линейного программирования.

Если целевая функция (1) и (или) хотя бы одна из функций в (2) являются нелинейными, то задача (1), (2) решается методами нелинейного программирования.

Если требуется, чтобы решение задачи (1), (2) выражалось целыми числами, то применяют методы целочисленного программирования.

Если в (1) или в (2) содержатся случайные величины, то задача решается методами стохастического программирования.

Также еще существует выпуклое, параметрическое и динамическое программирование.

В данной работе «Методы и модели в экономике» мы рассмотрим некоторые разделы линейного программирования.

 

Часть I. Геометрический метод. Симплекс-метод

Задача использования ресурсов

Предположим, что предприятие выпускает два вида продукции P1 и P2, используя для их производства 3 вида ресурсов S1, S2, S3. Запас ресурсов и количество единиц ресурса, используемых на производство единицы продукции, приводятся в следующей таблице:

 

Ресурс	Запас ресурса	Количество единиц ресурса, затрачиваемых на изготовление единицы продукции
P1	P2
S1
S2
S3			–

 

В этой таблице, например, значение 2 в последнем столбце есть количество единиц первого ресурса S1, используемых на производство единицы продукции P2.

Реализация одной единицы продукции P1 приносит прибыль в 5 у.е., P2 соответственно – 7 у.е. Необходимо выяснить, какое количество каждого вида продукции нужно выпустить для того, чтобы суммарная прибыль была наибольшей.

Прежде чем решать подобные задачи, необходимо составить так называемую экономико-математическую модель задачи, т. е. записать на математическом языке условия задачи. Для этого введем следующие обозначения.

Обозначим через план производства каждого вида продукции. Из первой строки таблицы видно, что на выполнение плана производства нам необходимо затратить ресурс S1 в количестве , ресурс S2 в количестве , и ресурс S3 в количестве . В силу ограниченности ресурсов должна выполнятся следующая система неравенств:

Количество произведенной продукции каждого вида не может быть отрицательным. Следовательно

Общая прибыль, которую мы получим после реализации всего количества произведенной продукции, запишется:

Таким образом, задача заключается в нахождении 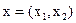, удовлетворяющего вышеуказанным системам неравенств, при котором функция F принимает максимальное значение.

Обобщим указанный пример на произвольный случай. Предположим, что предприятие производит n видов продукции и при этом использует m видов ресурсов . На изготовление одной единицы продукции затрачивается ресурса в количестве . Запас ресурсов предприятия ограничен значениями . Прибыль от реализации единицы продукции каждого вида равна .

Необходимо выяснить, какое количество каждого вида продукции требуется выпустить для того, чтобы суммарная прибыль была наибольшей.

Обозначим через план производства каждого вида продукции. Составим экономико-математическую модель. Необходимо найти , удовлетворяющего системе ограничений:

 

,

такого, что функция:

принимает максимальное значение.