Главная | Обратная связь

Примеры решения задач

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

 

Сила постоянного тока

I = q/t,

где q – заряд, прошедший через поперечное сечение проводника за время t.

Плотности тока

j = I/S,

где S – площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью <υ> направлен­ного движения заряженных частиц

j = qn<υ>,

где q – заряд частицы; n – концентрация заряженных частиц.

Закон Ома:

а) для участка цепи, не содержащего ЭДС, где φ₁ – φ₂ = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;

б) для участка цепи, содержащего ЭДС, где – ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) для замкнутой (полной) цепи, где R – внеш­нее сопротивление цепи; R_i – внутреннее сопротивление цепи.

Законы Кирхгофа:

а) ∑ I_i = 0 – первый закон;

б) ∑ I_iR_i = ∑ – второй закон,

где ∑ I_i – алгебраическая сумма сил токов, сходящихся в узле; ∑ I_iR_i – алгебраическая сумма произведений сил токов на сопротивление уча­стков; ∑ e_i – алгебраическая сумма ЭДС.

Сопротивление R и проводимость G проводника

R = ρl/S, G=γS/l,

где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.

Сопротивление системы проводников:

а) R = ∑ R_i при последовательном соединении;

б) 1/R = ∑(1/R_i) при параллельном соединении, где R_i – сопро­тивление i-го проводника.

Работа тока

A = IUt, A = I²Rt, A = U²t/R.

Первая формула справедлива для любого участка цепи, на кон­цах которого поддерживается напряжение U, последние две – для уча­стка, не содержащего ЭДС.

Мощность тока

P = IU, P = I²R, P=U²/R.

Закон Джоуля – Ленца

Q = I²Rt.

Закон Ома в дифференциальной форме

= γ ,

где γ – удельная проводимость; – напряженность электрического поля; –плотность тока.

 

Примеры решения задач

Пример 1. На тонком стержне длиной l = 20 см находится рав­номерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится то­чечный заряд q₁ = 40 нКл, который взаимодействует со стержнем с си­лой F = 6 мкН. Определить линейную плотность τ заряда на стержне.

Р е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом q₁ зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 1) малый участок dr с зарядом dq = τdr. Этот заряд можно рас­сматривать как точечный. Тогда, согласно закону Кулона,

Интегрируя это выражение в пределах от до + , полу­чаем

 

откуда

Проверим, дает ли расчетная формула единицу линейной плот­ности электрического заряда. Для этого в правую часть формулы вме­сто символов величин подставим их единицы:

 

Найденная единица является единицей линейной плотности заряда.

Произведем вычисления:

Пример 2.По тонкому кольцу равномерно распределен заряд q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напря­женность электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстоянии, равное половине радиуса.

 

 

Р е ш е н и е. Совместим координатную плоскость xOy с плос­костью кольца, а ось Oz – с осью кольца (рис. 2). На кольце выделим малый участок длиной dl. Так как заряд dq=τdl, находящийся на этом участке, можно считать точечным, то напряженность d электриче­ского поля, создаваемого этим зарядом, может быть записана в виде

 

где – радиус-вектор, направленный от элемента dl к точке А.

Разложим вектор d на две составляющие: d ₁, перпендику­лярную плоскости кольца (сонаправленную с осью Oz), и d ₂, парал­лельную плоскости кольца (плоскости xOy), т. е.

.

Напряженность электрического поля в точке А найдем интегрированием:

где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dq и dq` (dq = dq`), расположен­ных симметрично относительно центра кольца, векторы d ₂ и d ₂` в точке А равны по модулю и противоположны по направлению: d <sub>2</sub> = - d <sub>2</sub>`. Поэтому векторная сумма (интеграл) Составляю­щие d ₁ для всех элементов кольца сонаправлены с осью Oz (единич­ным вектором ), т. е. d ₁= dE₁. Тогда

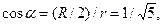Так как и то

Таким образом,

Из соотношения q = 2πRτ определим радиус кольца R = q/(2πτ). Тогда

Модуль напряженности

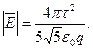(1)

Проверим, дает ли правая часть полученного равенства еди­ницу напряженности (В / м):

Выразим физические величины, входящие в формулу (1), в единицах СИ (τ = 5·10^-8 Кл/м, q=4·10^-8 Кл, ε₀ = 8,85·10^-12 Ф/м) и произ­ведем вычисления:

 

Пример 3.Две концентрические проводящие сферы радиу­сами R₁ = 6 см и R₂ = 10 см несут соответственно заряды q₁ = 1нКл и q₂ = - 0,5нКл. Найти напряженность Е поля в точках отстоящих от цен­тра сфер на расстояниях r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить гра­фик E(r).

 

Р е ш е н и е. Заметим, что точки, в которых требуется найти напря­женности электрического поля, лежат в трех областях (рис. 3): об­ласти I (r₁<R₁), области II (R₁<r₂<R₂), области III (r₂>R₂).

1. Для определения напряженности Е₁ в области I проведем гаус­сову поверхность S₁ радиусом r₁ и воспользуемся теоремой Остроград­ского – Гаусса:

(так как суммарный заряд, находящийся внутри гауссовой поверхно­сти, равен нулю). Из соображений симметрии E_n=E₁=const. Следова­тельно, и Е₁ (напряженность поля в области I) во всех точ­ках, удовлетворяющих условию r₁<R₁, будет равна нулю.

2. В области II гауссову поверхность проведем радиусом r₂. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум))

(так как внутри гауссовой поверхности находится только заряд q₁).

Так как E_n = E = const, то Е можно вынести за знак интеграла:

или ES₂ = q₁/ .

Обозначив напряженность Е для области II через Е₂, получим

Е₂ = q₁/( S₂),

где S₂ = 4πr₂² – площадь гауссовой поверхности. Тогда

(1)

3. В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность Е области III через Е₃ и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен q₁ + q_2. Тогда

Е₃ = (q₁+q₂)/4π r₃².

Заметив, что q₂<0, это выражение можно переписать в виде

(2)

Убедимся в том, что правая часть равенства (1) и (2)дает единицу на­пряженности:

Выразим все величины в единицах СИ (q₁ = 10^-9 Кл, q₂= - 0,5·10^-9 Кл, r₁=0,09 м, r₂=0,15 м, 1/(4πε₀)=9·10⁹ м/Ф) и произведем вычисления:

Построим график E(r). В области I(r₁<R₁) Е = 0. В области II (R₁ r<R₂) E₂(r) изменяется по закону 1/r². В точке r = R₁ напряжен­ность E₂(R₁) = q₁/(4π R₁²)=2,25 кв/м. В точке r = R₂ (r стремится к R₂ слева) E₂(R₂) = q₁/(4π R₂²) = 0,9 кВ/м. В области III (r>R₂) E₃(r) изменяется по закону 1/r², причем в точке r = R₂ (r стремится к R₂ справа) E₃(R₂) = (q₁ - |q₂|/(4π R₂²) = 0,45 кВ/м. Таким образом, функ­ция E(r) в точках r = R₁ и r = R₂ терпит разрыв.

График зависимости E(r) представлен на рис. 4.

 

 

Пример 4.Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии ₁ = 0,5 см и ₂ = 2 см от поверхности цилиндра, в средней его части.

Р е ш е н и е. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и измене­нием потенциала: = -grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

E = - dφ/dr, или dφ = - Edr.

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r₁ и r₂ от оси цилиндра:

(1)

 

 

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженно­сти поля можно воспользоваться формулой напряженности поля, соз­даваемого бесконечно длинным цилиндром:

E = τ/(2π r).

Подставив выражение Е в (1), получим

или

φ₁ – φ₂ = τ/(2π )ln(r₂/r₁). (2)

Произведем подстановку, учитывая, что величины r₁ и r₂, входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r₁ = R + = 1,5 см r₂ = R + = 3 см):

φ₁ – φ₂ = 2 · 10 ^–8 ·1,8 · 10¹⁰ ln(3/1,5) = 3,6 ·10² · 2,3 ln2 В = 250 В.

 

Пример 5.Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности потенциалов U₁ = 40 В. После отключения от источника тока конденсатор соединили с другим незаряженным конденсатором емко­стью С₂ = 5 мкФ. Какая энергия израсходуется на образование искры в момент присоединения второго конденсатора?

Р е ш е н и е. Энергия, израсходованная на образование искры,

= W₁ – W₂, (1)

где W₁ – энергия, которой обладает первый конденсатор до присоеди­нения к нему второго конденсатора; W₂ – энергия, которую имеет ба­тарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

W = ½СU², (2)

где С – емкость конденсатора или батареи конденсаторов.

Выразив в формуле (1) энергии W₁ и W₂ по формуле (2) и при­няв во внимание, что общая емкость параллельно соединенных кон­денсаторов равна сумме емкостей отдельных конденсаторов, получим

= ½ C₁U₁² – ½( C₁ + C₂)U₂², (3)

где U₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденса­тора остался прежним, выразим разность потенциалов U₂ следующим образом:

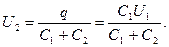
Подставив выражение U₂ в (3), найдем

или

Произведем вычисления:

Пример 6Потенциометр сопротивлением R = 100 Ом под­ключен к батарее с ЭДС e = 150 В и внутренним сопротивлением R_i = 50 Ом. Определить: 1) показание вольтметра между сопротивлением R_v = 500 Ом, соеди­ненного с одной из клемм потенциометра и подвижным контактом, установленным посе­редине потенциометра; 2) разность потен­циалов между теми же точками потенцио­метра при отключении вольтметра.

 

Р е ш е н и е. 1. Показание вольт­метра, подключенного к точкам А и В (рис. 12), определим по формуле

U₁ = I₁R₁,

где R₁ – сопротивление параллельно соединенных вольтметра и поло­вины потенциометра; I₁ – суммарная сила тока в ветвях этого соедине­ния (она равна силе тока в неразветвленной части цепи).

Силу тока I₁ найдем по закону Ома для полной цепи:

I₁ = e /(R_e +R_i), (1)

где R_e – сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:

R_e = R/2 +R₁. (2)

Сопротивление R₁ найдем по формуле параллельного соедине­ния проводников откуда

Подставив в (1) выражение R_e по (2), найдем

В данном случае решение задачи в общем виде было бы гро­моздким. Поэтому удобно вычисление величин провести раздельно:

U₁ = 1,03·45·5 В = 46,9 В.

2. Разность потенциалов между точками А и В при отключен­ном вольтметре равна произведению силы тока I₂ на половину сопро­тивления потенциометра:

U₂ = I₂ ·R/2, (3)

где I₂ – сила тока в цепи при отключенном вольтметре. Ее определим по формуле

I₂ = e /(R + R_i).

Подставив выражение I₂ в (3), найдем

U₂ = e / (R + R_i)·R/2.

Произведем вычисления:

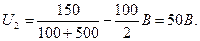
Пример 7Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I₀ = 0 до I = 6 А (рис 13). Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение q₁/q₂.

 

 

Р е ш е н и е. Закон Джоуля – Ленца в виде Q = I²Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон спра­ведлив для бесконечно малого интервала времени и записывается в виде

dQ = I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В данном случае

I = kt, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

С учетом (2) формула (1) примет вид

dQ = k²Rt²dt. (3)

Для определения теплоты, выделившейся за конечный интер­вал времени Δt, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

Произведем вычисления:

Q₁ = 1/3 · 3² · 20(1 – 0) Дж = 60 Дж;

Q₂ = 1/3 · 3² · 20(8 – 1) Дж = 420 Дж.

Следовательно,

Q₂ / Q₁ = 420 / 60 = 7,

т. е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

 

Пример 8Пространство между пластинами плоского конден­сатора имеет объем V = 375 см³ и заполнено водородом, который час­тично ионизирован. Площадь пластин конденсатора S = 250 см². При каком напряжении U между пластинами конденсатора сила тока I, про­текающего через конденсатор, достигнет значения 2мкА, если концен­трация n ионов обоих знаков в газе равна 5,3 · 10⁷ см^–3. Принять под­вижность ионов b₊= 5,4 · 10 ^–4 м² / (В · с), b_-=7,4 · 10^-4 м²/(В · с).

Р е ш е н и е. Напряжение U на пластинах конденсатора свя­зано с напряженностью Е электрического поля между пластинами и расстоянием d между ними соотношением

U = Ed. (1)

Напряженность поля может быть найдена из выражения плот­ности тока

j = qn(b₊ + b_-)E,

где q – заряд иона.

Отсюда

Расстояние d между пластинами, входящее в формулу (1), най­дем из соотношения

d = V/S.

Подставив выражения Е и d в (1), получим

(2)

 

 

Проверим, дает ли правая часть полученной расчетной фор­мулы единицу напряжения:

Подставим в формулу (2) значения величин и произведем вы­числения:

ЭЛЕКТРОМАГНЕТИЗМ

 

Связь магнитной индукции с напряженностью магнитного поля

=μ μ ,

где μ — магнитная проницаемость изотропной среды; μ — магнитная постоянная. В вакууме μ =1, и тогда магнитная индукция в вакууме

.

Закон Био-Савара-Лапласа

d = или d= d,

где — магнитная индукция поля, создаваемого эле­ментом про­вода длиной dl с током ; - радиус-вектор, направленный от эле­мента проводника к точке, в которой определяется магнитная индук­ция; α — угол между ра­диусом-вектором и направлением тока в эле­менте про­вода.

Магнитная индукция в центре кругового тока

,

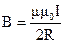где R — радиус кругового витка.

Магнитная индукция на оси кругового тока

,

 

где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

, ,

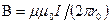где — расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (см. рис.1, а и пример 1),

Обозначения ясны из рисунка.

Направление вектора магнитной индукции обозначено точкой —это значит, что направлен перпендикулярно плоскости чертежа к нам.

При симметричном располо­жении концов провода относи­тельно точки, в которой опреде­ляется магнитная индукция (рис.1,б), , тогда

Магнитная индукция поля соле­ноида ,

где n — отношение числа витков соле­ноида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера),

, или ,

где l — длина провода; гол между направлением тока в проводе и вектором магнитной индукции . Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в от­дельности:

.

Магнитный момент плоского контура с током

,

где — единичный вектор нормали (положительной) к плоскости контура; I — сила тока, протекающего по кон­туру; S — площадь кон­тура.

Механический (вращательный) момент, действующий на контур с то­ком, помещенный в однородное магнитное поле,

 

, или ,

 

где α - угол между векторами и .

Потенциальная энергия (механическая)* контура с током в магнитном поле

 

, или .

 

Отношение магнитного момента 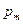к механическому L (мо­менту импульса) заряженной частицы, движущейся по крутой орбите,

 

,

 

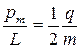где q - заряд частицы; m — масса частицы.

Сила Лоренца

 

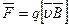, или ,

где— скорость заряженной частицы; — угол между векторами и .

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхно­сти

 

, или Φ = B S,

 

где S — площадь контура; α — угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

 

Ф = B dS

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток)

 

Ψ = ΝΦ.

 

Эта формула верна для соленоида и тороида с равномер­ной намоткой плотно прилегающих друг к другу N вит­ков.

Работа по перемещению замкнутого контура в магнитном поле

 

А = .

 

ЭДС индукции

.

Разность потенциалов на концах провода, движущегося со скоростью в магнитном поле,

 

,

 

где — длина провода; α — угол между векторами и . Заряд, протекающий по замкнутому контуру при из­менении магнитного по­тока, пронизывающего этот контур,

, или ,

 

где R — сопротивление контура.

Индуктивность контура

.

ЭДС самоиндукции

.

Индуктивность соленоида

,

где n — отношение числа витков соленоида к его длине; V — объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопро­тивлением R и индуктивностью L:

а) (при замыкании цепи), где — ЭДС источника тока; t — время, прошедшее после замыкания цепи;

б) (при размыкании цепи), где - сила тока в цепи при t =0; t — время, прошедшее с момента размыкания цепи.

Энергия магнитного поля

.

Объемная плотность энергии магнитного поля (отно­шение энергии магнитного поля соленоида к его объему)

=ВH/2, или = /(2 ), или = ,

где В — магнитная индукция; H — напряженность маг­нитного поля.

 

Пример 1. По отрезку прямого провода длиной l = 80 см течет ток Определить магнитную индукцию поля, создаваемого этим током, в точке A, равноудаленной от концов отрезка провода и находящейся на расстоянии = 30 см от его середины.

Решение. Для решения задач воспользуемся законом Био-Савара-Ла­пласа и принципом суперпо­зиции магнитных полей. Закон Био-Савара-Лапласа позволяет определить магнитную индукцию d, создавае­мую элементом тока Id. Заметим, что вектор dв точ­ке А направлен за плоскость чертежа. Принцип суперпозиции позволяет для определе­ния воспользоваться геометрическим суммированием (интегрированием):

= , (1)

где символ l означает, что интегрирование распространяется на всю длину провода.

Запишем закон Био-Савара-Лапласа в векторной форме:

,

где – магнитная индукция, создаваемая элементом провода дли­ной с током I в точке, определяемой радиусом-вектором ; – магнитная постоянная; – магнитная проницаемость среды, в кото­рой находится провод (в нашем случае ). Заметим, что векторы от различных элементов тока сонаправлены (рис. 2), поэтому выраже­ние (1) можно переписать в скалярной форме:

,

где

dB = dl.

В скалярном выражении закона Био-Савара-Лапласа угол α есть угол ме­жду элементом тока Idи радиусом-вектором .Таким образом,

 

(2)

 

Преобразуем подынтегральное выра­жение так, чтобы была одна перемен­ная – угол α. Для этого выразим длину элемента провода dl через угол

dα: dl = r dα/sin α (рис.2).

 

 

Тогда подынтегральное выраже­ние dl запишем в виде . Заметим, что пере­менная 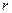также зависит от α, (r=r_o/sin ); следовательно,

= .

Таким образом, выражение (2) можно пе­реписать в виде

,

где 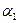и – пределы интегрирования. Выполним интегрирование:

 

. (3)

Заметим, что при симметричном расположении точки А относительно

отрезка провода С учетом этого формула (3) при­мет вид

. (4)

Из рис. 2 следует

Подставив выражение cos 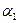в формулу (4), получим

. (5)

Произведя вычисления по формуле (5), найдем В = 26,7 мкТл.

Направление вектора магнитной индукции поля, создаваемого пря­мым током, можно определить по правилу буравчика (правилу правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рис. 3) и по касательной к ней в интересующей нас точке проводим вектор . Вектор магнитной индукции в точке А (см. рис. 2) направлен перпендикулярно плоскости чертежа от нас.

Пример 2. По тонкому проводящему кольцу радиусом R=10 см течет ток I = 80 А. Найти магнитную индукцию в точке A, равноудален­ной от всех точек кольца на расстояние r =20 см.

Решение. Для решения задачи воспользуемся законом Био-Савара-Ла­пласа:

,

где – магнитная индукция поля, создаваемого элементом тока в точке, определяемой радиусом-вектором .

Выделим на кольце элемент и от него в точку А проведем радиус-вектор (риc. 4). Вектор направим в соответствии с пра­вилом буравчика.

Согласно принципу суперпозиции магнитных полей,

магнитная индукция в точке А определяется интегрированием

,

где интегрирование ведется по всем элементам кольца.

Разложим вектор на две составляющие: , перпендику­лярную плоскости кольца, и d_║ , параллельную плоскости кольца, т. е.

 

.

 

Тогда

.

Заметив, что из соображений симметрии и что векторы от различных элементов сонаправлены, заменим векторное суммирование (интегрирование) скалярным:

,

где и (поскольку перпендикуля­рен и, следовательно, ). Таким образом,

.

После сокращения на 2π и замены cos β на (рис. 5) получим

Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл):

Здесь мы воспользовались определяющей формулой для магнитной индукции:

Тогда

.

Выразим все величины в единицах СИ и произведем вычисле­ния:

или В = 62,8 мкТл.

Вектор направлен по оси кольца (пунктирная стрелка на рис. 4) в соответствии с правилом буравчика.

 

Пример 3. Бесконечно длинный провод изогнут так, как это изобра­жено на рис. 5. Радиус R дуги окружности равен 10см. Определить магнитную индукцию поля, создаваемого в точке О током , текущим по этому проводу.

Решение. Магнитную индукцию в точке О найдем, используя прин­цип суперпозиции магнитных полей: В нашем случае про­вод можно разбить на три части (рис. 6): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружно­сти (2) радиуса R. Тогда

,

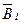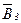где , и – магнитные индукции в точке О, создаваемые то­ком, текущим соответственно на первом, втором и третьем участках провода.

Так как точка О лежит на оси провода 1, то и тогда

Учитывая, что векторы ₂ и ₃ направлены в соответствии с прави­лом буравчика перпендикулярно плоскости чертежа от нас, то геомет­рическое суммирование можно заменить алгебраическим:

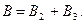
Магнитную индукцию В₂ найдем, воспользовавшись выраже­нием для магнитной индукции в центре кругового тока:

В нашем случае магнитное поле в точке О создается лишь половиной такого кругового тока, поэтому

Магнитную индукцию В₃ найдем, воспользовавшись соотно­ше­нием (3), выведенным в примере 1:

В нашем случае ( ), ,

тогда

Используя найденные выражения для В₂ и В₃, получим

или

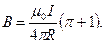
Произведем вычисления:

Тл = Тл,

или

В = 331 мкТл.

 

 

Пример 4. Протон, прошедший ускоряю­щую разность потенциалов U = 600 В, вле­тел в однородное магнитное поле с индук­цией В = 0,3 Тл и начал двигаться по ок­ружности. Вычислить радиус R окружности.

 

Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной ин­дукции

Так как сила Лоренца перпендикулярна вектору , то она сообщит частице (протону) нормальное ускорение .

Согласно второму закону Ньютона,

, (1)

где m – масса протона.

На рис. 7 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора . Силу Лоренца направим перпендикулярно вектору к центру окружности (векторы и сонаправлены). Используя правило левой руки, определим направле­ние магнитных силовых линий (направление вектора ).

Перепишем выражение (1) в скалярной форме (в проекции на радиус):

. (2)

В скалярной форме В нашем случае и , тогда Так как нормальное ускорение то выражение (2) перепишем следующим образом:

 

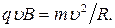
Отсюда находим радиус окружности

.

Заметив, что есть импульс протона (p), это выражение можно записать в виде

. (3)

Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. , или

где – ускоряющая разность потенциалов (или ускоряющее напряжение U); Т₁ и Т₂ – начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией протона и выразив кинетическую энергию Т₂ через импульс p, получим

Найдем из этого выражения импульс и подставим его в формулу (3):

или

(4)

Убедимся том, что правая часть равенства дает единицу длины (м):

Подставим в формулу (4) числовые значения физических вели­чин и произведем вычисления:

мм.

 

Пример 5. Электрон, влетев в однородное магнитное поле (В = 0,2 Тл), стал двигаться по окружности радиуса R = 5см. Определить магнитный момент эквивалентного кругового тока.

 

Ρ е ш е н и е. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. На рис.8 линии маг­нитной индукции перпендикулярны плоскости чертежа и направлены «от нас» (обозначены крестиками).

Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением

где 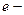заряд электрона; Т- период его обращения.

Период обращения можно выразить через скорость электрона и путь, проходимый электроном за период Тогда

. (1)

Зная найдем магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается со­отношением

(2)

где S – площадь, ограниченная окружностью, описываемой электроном

Подставив 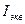из (1) в выражение (2), получим

Сократим на и перепишем это выражение в виде

(3)

В полученном выражении известной является скорость элек­трона, которая связана с радиусом R окружности, по которой он дви­жется, соотношением (см. пример 4). Заменив q на найдем интересующую нас скорость и подставим ее в формулу (3):

Убедимся в том, что правая часть равенства дает единицу маг­нитного момента :

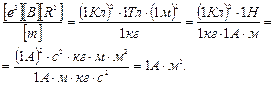
Произведем вычисления:

 

Пример 6. Электрон движется в однородном магнитном поле (В = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость υ.

Решение. Электрон будет двигаться по винтовой линии, если он вле­тает в однородное магнитное поле под некоторым углом ( ) к линиям магнитной индукции. Разложим, как это показано на рис.9, скорость электрона на две составляющие: параллельную вектору и перпендикулярную ему ( 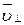). Скорость в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль си­ловой линии. Скорость 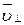в результате действия силы Лоренца будет изменяться только по направлению ( ) (в отсутствие парал­лельной составляющей ( ) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным сило­вым линиям). Таким образом, электрон будет участвовать одновре­менно в двух движениях: равномерном перемещении со скоростью и равномерном движении по окружности со скоростью .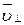

Период обращения электрона связан с перпендикулярной со­ставляющей скорости соотношением

. (1)

Найдем отношение 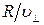. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение . Согласно второму закону Ньютона можно написать

или

(2)

где

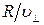Сократив (2) на выразим соотношение ( ) и подставим его в формулу (1):

Убедимся в том, что правая часть равенства дает единицу вре­мени (с):

Произведем вычисления:

Модуль скорости 12Следующая ⇒