Главная | Обратная связь

Тестовые задания по дисциплине

"Вычислительная математика"

1. Для заданной таблицы определить максимальный порядок j для конечной разности Δ^j x(t=1)

Варианты ответа:

1. j=1; 2. j=_2; 3. j=3.

__________________________________________________________________________________________

2. Для заданной таблицы определить максимальный порядок j для разделенной разности Δ^j x(t=1)

Варианты ответа:

1. j=1; 2. j=_2; 3. j=3.

____________________________________________________________________________________________

3. Для заданной сеточной функции построить таблицу разделенных разностей

Варианты ответа:

1_

i	ti	xi	x(ti, ti+1)	x(ti,ti+1,ti+2)	x(ti,ti+1,ti+2,ti+3)
	-2		1/3	-7/12	1/72
			3/2	-5/8
	-1		-1
		-1

2.

i	ti	xi	x(ti, ti+1)	x(ti,ti+1,ti+2)	x(ti,ti+1,ti+2,ti+3)
	-2		-1/3	-7/12	-1/72
			3/2	-5/8
	-1		-1/2
		-1

3.

i	ti	xi	x(ti, ti+1)	x(ti,ti+1,ti+2)	x(ti,ti+1,ti+2,ti+3)
	-2		1/3	7/12	-1/72
			3/4	-5/8
	-1
		-1

 

________________________________________________________________________________

4.Для заданной таблицы определить степень алгебраического интерполяционного полинома

Ответ: 1, 3, 2, 5.

________________________________________________________________________________

5.

Варианты ответа:

1_. ;

2. ;

3.

__________________________________________________________________________________

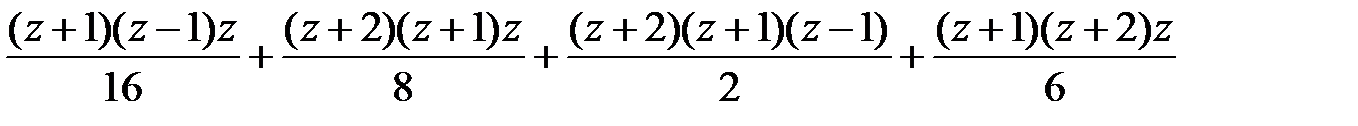
6. По формуле Ньютона построить интерполяционный полином для табличной функции x_i = f(t_i)

Варианты ответа:

1._ ;

2. ;

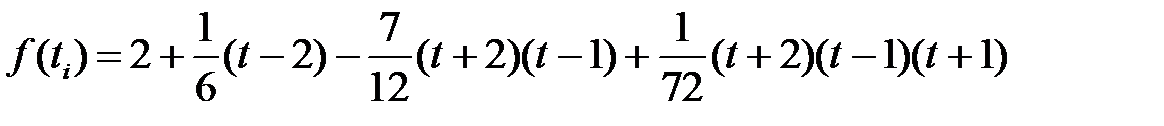3. .

____________________________________________________

7.(3)

Ответ: у₁=(2,1,0,0)^T; у₂=(1/5,-2,1,0)^T. у₃=(-1/6,1,1/6,1)^T

у₁=(2,1,0,0)^T; у₂=(1/5,5,1,0)^T. у₃=(-1/6,1,6,1)^T

у₁=(2,1,0,0)^T; у₂=(1/5,-2/5,1,0)^T. у₃=(-1/6,1/3,1/6,1)^T

______________________________________________________

8.(3)

Ответ: ψ₁=2k₁, ψ₁=k₂( x-1/2), ψ₁=k₃( x² – 4x+25/6);

ψ₁=1*k₁, ψ₁=k₂( x-3/2), ψ₁=k₃( x² – 5x+25/6);

ψ₁=1*k₄, ψ₁=k₂( x-5/2), ψ₁=k₃( x² – 5x+25/6);

k₁, k₂, k₃ – произвольные числа.

____________________________________________________

9.(2)

Ответ: 0,6+2x

0,5+1,95x

1+3x

_____________________________________________________

10.(1)

Ответ: 1 – 0,4x

2, 1 – 0,4x

1 – 1,4x

_____________________________________________________

11. n – число отрезков

Ответ: 1,2; 2,0;1,75; 2,6.

___________________________________________

12. n – число отрезков(2)

Ответ: 0,25; 0,26; 0,2; 0,8.

____________________________________________

13. n – число отрезков(2)

Ответ: 4,3; 5; 5,2; ;4,8.

____________________________________________

14. n – число отрезков(1)

Ответ: 2,5; 3; 2; 1,7.

__________________________________________________________

15.Найти линейно независимые решения однородной системы Ax=0,

Ответ: x=c(1 3,5 1 0)^T

x=c(1,5 3,5 1 0)^T

x=c(0,5 3,5 1 1)^T

c – произвольная числовая константа. (2)

_____________________________________________________________

16.Определить геометрическую кратность собственных чисел матрицы А.

Характеристическое уравнение матрицы

( + 5)³ = 0.

Ответ: 1; 2: 3. (1)

______________________________________________________________

17. Найти Жорданову форму матрицы А.

Характеристическое уравнение матрицы

³ = 0.

Ответ:

1._ ; 2. ; 3. .

________________________________________________________________________________

18.Рассчитать матрицу S преобразования в Жорданову форму J исходной матрицы А: J = S^-1AS.

 

,

Характеристическое уравнение матрицы A

( + 5)³ = 0.

,

Правильность результата подтвердить проверкой условий

det(S) ≠ 0, AS=SJ.

_____________________________________________________

19.Вычислить матричную экспоненту e^At, t – cкаляр.

,

Жорданова форма J = S^-1AS:

,

Матрица S:

.

Правильность расчета проверить с помощью встроенной функции Matlab expm(A).

_____________________________________________________________________

20. Определить условия совместности системы Ax = b, где

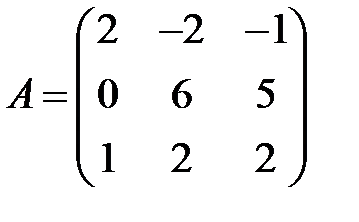, b = (b₁ b₂ b₃)^T.

Ответ: (1)

-b₁ + 2b₂ - b₃ = 0

-b₁ + b₂ - b₃ = 0-b₁ + 2b₂ - b₃ = 0

-b₁ - 2b₂ - b₃ = 0

__________________________________________________________________________

21. Используя метод Гаусса, решить систему линейных алгебраических уравнений Ax = b.

, b =(10 3 8)^T.

Ответ: (2)

x =(1 3 8)^T

x =(1 1 1)^T

x =(1 3 2)^T

___________________________________________________________________________

22. Рассчитать матрицы P, L. U в LU разложении A = PLU.

.

Правильность расчетов подтвердить перемножением PLU.

____________________________________________________________________________

23. Решить систему линейных алгебраических уравнений Ax = b.

, b =(13 12 13)^T, используя известное LU разложение матрицы A;

L =

1 0 0

1/10 1 0

1/10 81/151 1

U =

10 9 -6

0 151/10 -22/5

0 0 900/151

P =

1 0 0

0 1 0

0 0 1

Ответ: (2)

x =(1 3 8)^T

x =(1 1 1)^T

x =(1 3 2)^T

_____________________________________________________________________________

24. В разложении A = QR матрицы Q и R обладают следующими свойствами.

Варианты ответов: 1.Q ортогональная, R верхняя треугольная.

2.Q нижняя треугольная, R верхняя треугольная.

3. Q ортогональная, R треугольная с единицами на главной диагонали.

_______________________________________________________________________________

25.Решить систему линейных алгебраических уравнений Ax = b.

, b =(13 12 13)^T, используя известное QR разложение матрицы А.

_{Q =}

_{-201/203 844/6301 -961/23544}

_{-201/2030 -1157/1321 -2883/6104}

_{-201/2030 -1166/2515 1525/1732}

_R=

_{-2030/201 -4623/406 6673/1087}

_{0 -3515/207 1573/720}

_{0 0 5059/964}

Ответ: (2)

x =(1 3 8)^T

x =(1 1 1)^T

x =(1 3 2)^T.

__________________________________________________________________________________

26.Используя функцию eig из символьного пакета Matlab рассчитать собственные числа матрицы А.

Определить алгебраическую и геометрическую кратности каждого собственного числа.

.

______________________________________________________________________________________________________________________________

27. Используя язык программирования Matlab, записать программу, реализующую QR алгоритм. С её помощью найти собственные числа матрицы А.

.

_______________________________________________________________________________________________________________________________

28. Определить минимальный многочлен матрицы А, используя функцию eig из символьного пакета Matlab.

.

Убедится в правильности расчетов подстановкой матрицы А в найденный многочлен.

_________________________________________________________________________________________________

29.Воспользовавшись многочленом Лагранжа – Сильвестра, вычислить f(At) = e^At для матрицы

с минимальным многочленом ψ(λ) = (λ – 1)² (λ – 2).

___________________________________________________________________________________________________

30. Заменить дифференциальное уравнение

12y'''(t)+106y''(t)+5y'(t)+y = 10; н. у.: y(0) = y'(0) = y''(0) = 0; t ∈ [0,200].

эквивалентной системой дифференциальных уравнений первого порядка.

____________________________________________________________________________________________________

31. Используя функцию ode45 Matlab, найти решение задачи Коши для дифференциального уравнения

12y'''(t)+106y''(t)+5y'(t)+y(t) = 10; н. у.: y(0) = y'(0) = y''(0) = 0; t ∈ [0,200].

Построить график y(t).

_____________________________________________________________________________________________________

 

32. Система дифференциальных уравнений устойчива (неустойчива)?

Варианты ответов: 1. по Ляпунову; 2.Асимптотически; 3. Неустойчива.

_______________________________________________________________________________________

33. Система разностных уравнений устойчива (неустойчива)?

Варианты ответов: 1. по Ляпунову; 2.Асимптотически; 3. Неустойчива.

___________________________________________________________________________________________

34. Преобразовать уравнение x⁵ – x+x³ – 0.2 = 0 к виду, пригодному для решения методом простых итераций.

Варианты ответов: 1. x⁵ = x - x³ – 0.2 ; 2. x⁵ – x+x³ = 0.2 -x⁵ + x; 3. x = x⁵ +x³ – 0.2 .

____________________________________________________________________________________________

35. Условия сходимости при решении системы уравнений x = φ(x) имеет вид?

Варианты ответов 1. 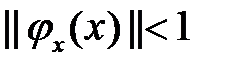; 2 : 3. .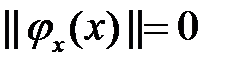

_____________________________________________________________________________________________________________________

36. Используя язык программирования Matlab, составить программу, реализующую метод Ньютона решения системы нелинейных уравнений.

Решить систему

x²y² – 3x³ – 6y³ + 8 = 0

x⁴ – 9y +2 = 0

ε ≤ 10^-4.

______________________________________________________________________________________________________________________

37.Используя средства системы Matlab решить систему уравнений

.

Указание: применить функцию svd – сингулярное разложение.