Главная | Обратная связь

Требуется из круговых секторов данного периметра 2р найти такой, площадь которого была бы наибольшей.

Решение

Пусть х – длина дуги сектора. По периметру и длине дуги сектора легко найти радиус, он равен ½(р-х). Площадь сектора выражается функцией S=¼(2р-х)х или S= - ¼х²+ ½рх. По теореме об экстремумах квадратичной функции найдём, что при х₀=р получившаяся функция принимает наибольшее значение следовательно, из всех круговых секторов с данным периметром 2р наибольшую площадь, равную ¼р², имеет сектор, дуга которого равна полупериметру ( а значит и сумме двух радиусов).

 

Обратимся к функции третьей степени у=ах³+вх+сх+с², где а, в, с и d- действительные числа и а≠0. Чтобы найти локальные экстремумы этой функции, введем в рассмотрение прямую у= h. При различных значениях h эта прямая может иметь с графиком данной функции третьей степени одну точку пересечения, или три, или наконец одну точку пересечения и одну точку касания нас интересует последняя возможность. Имея систему уравнений,

у=ах³+вх²+сх+d

у= h

получаем уравнение:

h =ах³+вх²+сх+d ,или

ах³+вх²+сх+d- h=0.

Если через х₀ обозначить абсциссу точки пересечения графика рассматриваемой функции и прямой у= h ,то х₀ является корнем уравнения ах³+вх²+сх+d- h=0 и поэтому можно понизить степень уравнения. Разделив ах³+вх²+сх+d- h=0 на х-х₀, получим частное ах²+(ах₀+в)х+ах₀²+вх₀+с и остаток ах₀³+вх₀²+сх₀+d-h. Так как х₀ – корень уравнения, то остаток должен быть равен 0, то есть ах₀³+вх₀²+сх₀+d-h=0. Частное же должно иметь два равных корня, так как нас интересует точка касания. Корни частного таковы

Чтобы они оказались равными, должно быть

. Откуда

При этих значениях х₀ абсцисса точки касания (х₁=х₂) будет равна

или (*)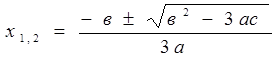

 

То обстоятельство, что нашлись два значения для х₀ и два значения абсцисс точек касания, объясняется тем, что прямая у=h касается графика данной функции дважды (Значит, если функция третьей степени имеет локальные экстремумы, то их обязательно два и один из них максимум, а другой минимум. Если а>0, то максимум будет при х, равном меньшей дроби (*), а минимум – большей. Если же а<0, то наоборот.

 

Применение производной к решению задач на экстремумы

Общий метод решения задач на экстремум опирается на теорему Ферма.

 

Если функция y=f(x) (имеющая производную) при х=х₀принимает локальный максимум или минимум, то производная от этой функции при х=х₀обращается в ноль.

Эта теорема является лишь необходимым условием существования экстремума. Производная может быть равна нулю, но при этом значении х функция может и не иметь экстремума. На пример, производная функции y=x³ при х=0 обращается в ноль, но при х=0 экстремума не имеет. Значит, уравнение f ’(x)=0 даёт лишь «подозрительные» на экстремум значения.

Для случая когда функция f не только непрерывна на отрезке [a;b], но имеет на этом отрезке лишь конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значения f .

Предположим сначала, что f не имеет на отрезке [a;b] критических точек. Тогда она возрастает или убывает на этом отрезке, и, значит наибольшее и наименьшее значение принимает на концах отрезка.

Пусть теперь функция f имеет на отрезке [a;b] конечное число критических точек. Эти точки разбивают отрезок на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значение функции f на таких отрезках принимается в их концах, т.е. в критических точках функции или в точках a и b.

Таким образом, чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.

Поскольку общий метод включает в себя отыскание производных, то им могут пользоваться лишь учащиеся старших классов, знакомые с дифференцированным исчислением.

При формировании у учащихся понятия о решении задач на наибольшее и наименьшее значение, при использовании основного метода можно воспользоваться решёнными ранее задачами, и показать на их примере применение общего метода.

Например, задача о тоннеле наибольшей пропускной способности.

Уже известно, что функция которая задаёт формализацию этой задачи имеет вид y=-(2+p/2)x²+2px.

Найдём производную этой функции y=-(4+p)x+2p приравняем её к нулю, получим -(4+p)x+2p=0 или

Задача 12