Главная | Обратная связь

Интеграция различных способов решения задач

Большинство школьных задач на отыскание наибольших и наименьших значений геометрических величин сводится к исследованию функции от одной переменной. Учащиеся с интересом решают экстремальные задачи на уроках и внеклассных занятиях. Их часто предлагают и на вступительных экзаменах в высшие учебные заведения.

При решении задачи на экстремум учащиеся нередко испытывают трудности в составлении аналитической записи функции, описывающей условие задачи. Причиной этому часто бывает нерациональный выбор независимой переменной. Ее желательно выбрать так, чтобы более коротким путем получить аналитическое выражение искомой функции и чтобы это выражение было по возможности более простым. Полезно показать учащимся на конкретном примере, что при удачном выборе аргумента функции удается сократить вычисления и упростить решение задачи.

а)В окружность радиуса R вписана трапеция ABCD, основание АВ которой является диаметром окружности. Какова должна быть длина боковой стороны трапеции, чтобы трапеция имела наибольшую площадь?

Решение 1

В задаче требуется найти длину боковой стороны трапеции, при которой площадь трапеции будет наибольшей. Площадь трапеции ABCD можно найти по формуле: , где DН – высота трапеции, или, так как трапеция равнобочная и , - по формуле: S=BH×DH.

Исходя из поставленной задачи, можно боковую сторону АD принять за независимую переменную х, затем через неё и радиус R окружности выразить площадь трапеции. Треугольник ABD прямоугольный, поэтому AD²=АВ×АН, откуда АН=х²/2R.

По теореме Пифагора , а так как , то .

По смыслу задачи 0<x<R . При x=R трапеция вырождается в равнобедренный треугольник.

Функция g(x)=8x(4R²-x²)³x² отличается от функции S² лишь постоянным множителем и имеет наибольшее значение одновременно с функцией S. Найдем производную g^’(x). В результате некоторых преобразований получим: g^’(x)=8х(4R²-x²)²(R²-x²).

В промежутке (0; R ) производная обращается в нуль лишь при х=R, меняя при этом знак плюс на минус. Значит, при х=R функция g(x) имеет наибольшее значение. Таким образом, площадь трапеции будет наибольшей при АD= R. Легко заметить, что искомая трапеция имеет форму половины правильного шестиугольника, площадь которого равна .

 

Ответ: R.

Решение 2

 

Обозначим через х высоту DH трапеции. Из прямоугольного треугольника ОDH (О – центр окружности) находим: . Значит, , и получим: , где 0<x<R.

 

Решение 3

 

Пусть ВН=х. Тогда АН= 2R-x. Согласно свойству высоты прямоугольного треугольника АВD имеем:

DН= .

Следовательно: , R<x<2R.

Производная функции S²=2Rx³-x⁴ находится проще, чем при решении задачи первым и вторым способом.

Заметим, что 3S²=(6R-3x) ×х×х×х.

Правая часть этого равенства представляет собой произведение переменных, сумма которых постоянна и равна 6R. Следовательно, это произведение принимает наибольшее значение в случае их равенства, т.е. х=6R-3x, откуда х=3R/2. При этом АН= R/2 и АD= ОD = R.

 

Решение 4

 

Пусть ÐВАD=х. Тогда ВD=2 Rsin x, BH=2Rsin²x, DH=2Rsin x×cos x.

Далее находим: S=4R²sin³x×cos x, где 45°<x<90°.

S¢=0 при tg x= , т.е. при х=60°. Остается сравнить значение функции S в критической точке со значениями на концах промежутка [45°;90°].

 

 

Решение 5

Введем независимую переменную ÐАОD=х. Площадь трапеции равна сумме площадей трех треугольников АОD, ВОС и СОD. Следовательно:

, 0°<x<90°.

Таким образом, задача легко сводится к нахождению наибольшего значения функции:

g(x)=2sin x+sin 2x.

Ее производная g¢(x)=2cos x+2cos 2x.

Критические точки получим, решив уравнение cos x+cos 2x=0 при 0°<x<90°.

Таким же способом можно решить более общую задачу:

б) Пусть в окружность вписан произвольный четырехугольник ABCD так, что АВ – диаметр окружности. Доказать, что площадь четырехугольника ABCD будет наибольшей, когда стороны ВС, CD и AD равны.

 

Решение

Обозначим ÐАОD=a, ÐВОС=b и ÐСОD=g. Тогда a+b+g=180°. В силу известного неравенства имеем:

sin a+sinb+sing£ .

Причем равенство достигается лишь при a=b=g=60°. Следовательно, площадь S будет наибольшей, когда ВС=СD=АD= R.

После разбора различных способов решения первой задачи учащимся можно предложить обобщение этой задачи.

 

в)В окружность радиуса R вписана трапеция ABCD с основанием АВ. При какой длине стороны AD площадь трапеции будет наибольшей, если ÐАОВ=a, где О – центр окружности?

 

Решение

Пусть ÐАОD=ÐВОС=х. Площадь треугольника АОВ равна . Выразим таким же образом площади треугольников АОD, СОD и ВОС.

Учитывая, что ÐСОD=360°-(a+2х), получим:

.

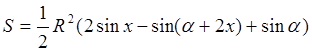Проведем диаметр MN окружности параллельно основанию АВ трапеции. Легко установить, что площадь трапеции не может быть наибольшей, если хорды АВ и CD будут лежать по одну сторону от MN. Поэтому следует считать, что 90°£х+a/2£180°, где 0<a£180°/

Функция S имеет наибольшее значение одновременно с функцией , где 90°-a/2£х£180°-a/2.

Найдем производную этой функции:

.

Учитывая границы изменения х, получаем:

или, несколько расширяя границы эти промежутков:

Следовательно, при всех допустимых значениях х имеем: и g¢(x)=0 тогда и только тогда, когда , откуда .

Итак, в промежутке [90°-a/2, 180°-a/2] функция g(x) имеет единственную критическую точку х₀, в которой производная меняет знак плюс на минус. Значит, в этой точке функция имеет максимум. Одновременно получаем и искомое наибольшее значение. Таким образом, площадь трапеции ABCD будет наибольшей в том случае, когда дуги ВС, СD и АD равны и АD=2Rsin(60°-a/6).

 

Нужно отметить, что при решении последней задачи для общего случая вычисления значений функции g(x) в граничных точках и сравнения их со значением в критической точке затруднительно, поскольку в выражение входит параметр a, но совсем легко доказать, что в критической точке производная меняет знак плюс на минус.

Как известно, решение задачи на отыскание наибольшего или наименьшего значения геометрической величины с помощью общего метода, основанного на применении производной, не всегда является лучшим. Иногда к цели можно прийти быстрее и более коротким путем, используя элементарные методы и приемы. «Следует иметь в виду, что бывают случаи, когда задача решается проще чисто геометрическим путем». [Гусев В.А., Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике. Геометрия. 2-е изд., перераб. и доп. М.: Просвещение, 1992]

 

г)Куб, ребро которого равно а, пересекается плоскостью, проходящей через его диагональ. Какую наименьшую площадь может иметь сечение и при каком угле наклона сечения к плоскости основания?

 

Решение 1

 

Пусть плоскость, проходящая через диагональ B₁D куба, пересекает его ребро AA₁ в точке K.Тогда она пересечет ребро CС₁ в точке L, симметричной K относительно центра куба. В сечении получится параллелограмм B₁KDL, площадь которого равна удвоенной площади треугольника B₁KD. Проведем высоту KM треугольника B₁KD. Введем обозначения: B₁D=d, DM=y, AK=x.

Площадь сечения определяется формулой: S=dh, где d=a . Следовательно, задача сводится к нахождению наименьшего значения h. Из прямоугольных треугольников B₁KM и DKM, выразив по теореме Пифагора двумя способами KM, получим уравнение:

(a²+x²)-y²=a²+(a-x)²-(d-y)²,

откуда y= .

Следовательно, .

Применив способ выделения полного квадрата, находим:

 

, где 0£ х£а.

Отсюда сразу следует, что h принимает наименьшее значение при х=а/2, равное , наименьшее значение площади сечения равно .

Угол j между плоскостью этого сечения и плоскостью основания ABCD куба найдем по формуле cos j=S_осн: S_сеч. Получим cos j= .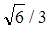

 

Ответ:

 

 

В пособии Гусева В.А. и др. (с.328-330) дано такое же по форме решение. Только площадь сечения вычисляется по формуле:

S_сеч=В₁K×KD×sina, где a=Ð В₁KD, а наименьшее значение площади сечения находится с помощью производной. Решение задачи оказывается более громоздким. Геометрическое решение в пособии не приводится.

 

Решение 2

 

Задача сводится к нахождению кратчайшего расстояния h между скрещивающимися прямыми AA₁ и B₁D . Так как ребро AA₁ параллельно плоскости BDB₁, т.е. равно высоте АР прямоугольного треугольника АBD. Получаем:

Следовательно, наименьшее значение площади сечения S=B₁D×AP= .

Угол наклона сечения к плоскости основания находится также, как и в первом случае.

 

Решение 3

Решение данной задачи упрощается, если использовать формулу:

, где j - угол между плоскостью сечения B₁KDL и плоскостью грани АBСD куба.

Построим линию пересечения этих плоскостей, прямую l, и проведем B₁Н^ l. По теореме о трех перпендикулярах BН^ l, следовательно Ð B₁НВ=j, 0°<j<90°. Площадь сечения будет наименьшей, когда сечение проведено так, что угол j - наименьший из возможных. Но , значит, j имеет наименьшее значение, когда ВН имеет наибольшее значение.

Поскольку катет прямоугольного треугольника меньше гипотенузы, то ВН£BD, и наибольшее значение ВН достигается в том случае, когда точки Н и D совпадают.

 

 

Преимущество геометрических способов решения становится еще более очевидным при решении следующей задачи, представляющей собой обобщение предыдущей.

 

д)Прямоугольный параллелепипед, измерения которого равны a,b,c пересекается плоскостью, проходящей через его диагональ. Какую наименьшую площадь может иметь сечение, если a£b£c?

Ответ:

е)В ромб с диагоналями d₁ и d₂ вписать прямоугольник наибольшей площади.

 

Решение

Вначале докажем следующие утверждения:

1) если параллелограмм вписан в другой параллелограмм, то их центры совпадают;

2) если прямоугольник вписан в ромб, то стороны прямоугольника либо параллельны диагоналям ромба, либо угол между диагоналями прямоугольника равен углу ромба.

 

Последней задаче целесообразно придать несколько другой вид: вместо диагоналей ромба задать его угол.

 

ж) В ромб с острым углом a вписать прямоугольник наибольшей площади.