Главная | Обратная связь

Метод Гаусса решения системы линейных алгебраических уравнений

Решение систем линейных алгебраических уравнений (СЛАУ) – наиболее часто встречаемая в научных вычислениях задача.

К системам линейных алгебраических уравнений так же приводят задачи аппроксимации.

Система линейных алгебраических уравнений с матрицей вещественных коэффициентов.

И вектором правых частей

Относительно неизвестного вектора

Записывается в координатной форме в следующей форме

Сокращённый вид координатной формы

Векторная форма

Каждое уравнение описывает прямую (n=2), плоскость (n=3), гиперплоскость (n>=4) в вещественном пространстве, поэтому решить систему – значит найти точку их пересечения в этом пространстве.

Будет предполагать, что определитель матрицы A отличен от нуля, то есть что решение существует и единственно.

Предположим, что

Разделим первое уравнение системы на , получим

Обозначим:

Получим

Или

Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент

Например, для второго уравнения

Коэффициенты при обозначим через , а правую часть – через

Тогда 2-е уравнение системы (1) имеет вид:

3-е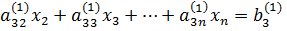

n-е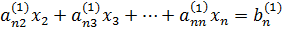

В результате получилась система из n-1 уравнений.

Более кратко форма записи полученной системы уравнений имеет вид:

Далее аналогичную процедуру выполняем с полученной системой из n-1 уравнений, только теперь делим первое уравнение этой системы на

Обозначим

Получаем

или

Затем из каждого и уравнений (2) вычитается первое уравнение, умноженное на соответствующий коэффициент

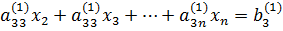
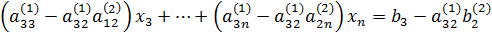
Коэффициенты при xj обозначим через , а правую часть – через

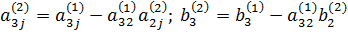
Тогда уравнение системы (2) примет вид

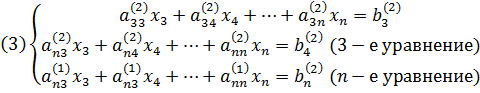
В результате получилась система из n-2 уравнений.

Более краткая форма записи системы уравнений примет вид

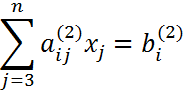
В результате приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали.

Завершаем прямой ход метода Гаусса.

Обратный ход метода Гаусса заключается в нахождении неизвестных , причём именно в порядке убывания индекса. 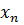уже определена из последнего уравнения, а общая формула обратного хода:

 

 

Билет 13