Основные числовые множества

N	{1,2,3,...,n} Множество всех натуральных чисел
Z	{0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных.
Q	Множество рациональных чисел. Кроме целых чисел имеются ещё и дроби. Дробь — это выражение вида , где p — целое число, q — натуральное. Десятичные дроби также можно записать в виде . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде . Например, в виде дроби со знаменателем "один": 2 = 2/1. Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической.
R	Множество всех вещественных чисел. Иррациональные числа — это бесконечные непериодические дроби. К ним относятся: § число — отношение длины окружности к её диаметру; § число — названное в честь Эйлера и др.; Вместе два множества (рациональных и иррациональных чисел) — образуют множество действительных (или вещественных) чисел.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой)множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

согласно «определению» множества, если один и тот же элемент содержится и в множестве А и в множестве В, то в их объединение этот элемент включается только один раз.

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

Операции с множествами удобно иллюстрировать при помощи графических схем, в которых отдельные множества представляются в виде кругов. Предполагается, что элементами множества являются все точки круга. Такие круги называются диаграммами Вена или кругами Эйлера.

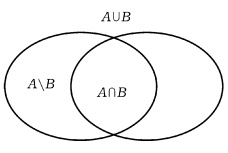
2.3.1. Объединение множеств

Объединением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т. е. принадлежат А, или принадлежат В, или принадлежат и Аи В. Объединение множеств А и В обозначается через АÈВ. Таким образом,

С=А∪В.

Напомним, что согласно «определению» множества, если один и тот же элемент содержится и в множестве А и в множестве В, то в их объединение этот элемент включается только один раз.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то А∪В={1, 2, 3, 4, 5, 6, 7}. Если А – множество отличников группы, а В – множество хорошистов, то АÈВсоставляет множество и отличников, и хорошистов. Если А – множество отличников группы, а В – все множество студентов группы, то элементами А∪В являются все студенты группы.

По аналогии с алгеброй чисел объединение иногда называют суммой множеств.

Если А – множество точек левого круга, а В – точек правого круга на рис.2.1, то заштрихованная фигура есть А∪В.

Рис. 2.1

2.3.2. Пересечение множеств

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству Водновременно. Объединение множеств А и В обозначается через А∩В. Таким образом,

С=А∩В

Т.е. пересечение множеств есть общая часть данных множеств.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то А∩В={2, 4}. Если А –множество отличников группы, а В – множество юношей, то А∩В составляетмножество юношей-отличников.

По аналогии с алгеброй чисел пересечение называют произведением множеств.

С помощью кругов Эйлера пересечение множеств А и В изображается следующим образом (заштрихованная часть на рис. 2.2.).

Рис. 2.2

2.3.3. Разность множеств

В отличие от объединения и пересечения множеств эта операция определяется только для двух множеств. Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В. Разность множеств А и В обозначается через А\В. Таким образом,

С=А\В

Например, если А={1, 2, 3, 4, 5}, а В={2, 4}, то А\В={1, 3, 5}. Если А –множество отличников группы, а В – множество юношей, то А\В составляетмножество девушек-отличников.

С помощью кругов Эйлера для случаев, изображенных на рис.2.5, разность множеств А и В изображается следующим образом (заштрихованная часть).

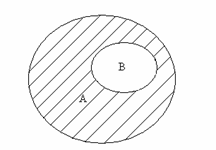
Рис. 2.5

Заметим, что разность множеств не является ни коммутативной, ни ассоциативной операцией.

2.3.4. Симметрическая разность множеств

Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств Аили В. Симметрическая разность множеств А и В обозначается через АDВ.

С=АDВ= (А\В)È (В\А).

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АDВ={1, 3, 5, 6, 7}. Если А – множество отличников группы, а В – множество юношей, то А\Всоставляет множество девушек-отличников и юношей-неотличников.

С помощью кругов Эйлера симметрическая разность множеств А и ВАDВ изображается следующим образом (заштрихованная часть на рис. 2.6).

Рис. 2.6

В отличие от разности множеств симметрическая разность является коммутативной, ассоциативной и дистрибутивной операцией:

АDВ = ВDА – коммутативность (переместительность);

(АDВ)DС = АD(ВDС) – ассоциативность (сочетательность);

(АDВ)ÇС = (АÇС) D (ВÇС) – дистрибутивность (распределительность).

E=∪ C= ∩

Пример 2.1. Найти АÈВ, АÇВ, А\В, В\А, АDВ, если А=[1, 3), а B=(2, 4].

Изобразим множества А и В на числовой прямой.

Рис. 2.7

Напомним, что если точка не входит во множество она обозначается «белой», если принадлежит множеству – «черной». Множество А обозначено штриховкой с наклоном вправо, множество В – штриховкой с наклоном влево.

Из рисунка видно, что объединением множеств А и В является множество АÈВ=[1, 4], пересечением множеств А и В – множество АÇВ=(2, 3). Разность множеств А\В=[1, 2]. (По определению это элементы множества А, исключая элементы множества В. Число 2 не входит в множество В, поэтому оно включается в А\В.) Аналогично, В\А=[3, 4]. Симметрическая разность АDВполучается путем объединения множеств А\В и В\А: АDВ=[1, 2] È [3, 4].

Пример 2.2. Даны множества А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, С={6, 7, 8, 9}. Найти множество (АÈВ) D (ВÈС).

Сначала найдем множества, стоящие в скобках АÈВ={1, 2, 3, 4, 5, 6, 7},ВÈС={2, 4, 6, 7, 8, 9}. Теперь вычтем из первого множества второе и из второго первое: (АÈВ)\(ВÈС)={1, 3, 5}, (ВÈС)\(АÈВ)= {8, 9}. Объединяя эти множества, получаем (АÈВ) D (ВÈС)={1, 3, 5, 8, 9}.

Достаточно часто круги Эйлера применяются для наглядного представления и последующего упрощения некоторого сложного выражения или совокупности условий на несколько множеств.

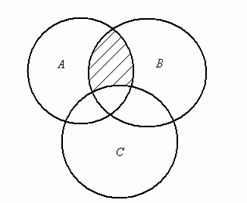
Пример 2.3. Заштрихуйте ту часть диаграммы, которая соответствует множеству (АÇВ)\С, для случая на рис. 2.8.

Рис. 2.8

Построение кругов Эйлера для сложного выражения, составленного для нескольких множеств посредством операций над ними, осуществляется комбинированием описанных способов построения для этих составных частей. Сначала изобразим пересечение множеств А и В (рис. 2.9.а)). А затем вычтем из (АÇВ) множество С (рис. 2.9.b)).

a) АÇВ b) (АÇВ)\С

Рис. 2.9

Пример 2.4. Пусть А и В такие множества, что А\В=В\А=Æ. Записать отношение между множествами А и В более простым способом.

Выражение А\В=Æ означает, что во множестве А нет элементов, которые не принадлежали бы В. Значит все элементы А принадлежат В. Это означает, чтоАÍВ (рис.2.10.а)). Аналогично, из выражения В\А=Æ следует, что ВÍА. Т.е. АÍВ иВÍА (рис.2.10.b)).

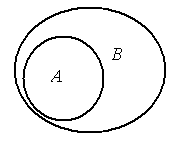
a) АÍВ b) ВÍА

Рис. 2.10

Таким образом, согласно свойству включений (2.3) А=В.