 |
|
Различные формы метода математической индукции
Система натуральных чисел. Аксиомы Пеано.
Для аксиоматического построения системы ℕ натуральных чисел вводят основные объекты, обозначаемые символами 1, а, b, c, …;между основными объектами вводят основное отношение – «'» (читается «непосредственно следовать за…»), т.е. а' - элемент, непосредственно следующий за элементом а.
Определение1. Непустое множество ℕ с определенным на нем отношением «'» («непосредственно следовать за...») называется натуральным рядом чисел, а его элементы - натуральными числами, если выполняютcя следующие аксиомы, называемые аксиомами Пеано:
(Р1). Существует натуральное число, обозначаемое символом 1, которое непосредственно не следует ни за одним натуральным числом, т.е. 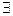 1
1 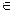 N такое что а'≠1,
N такое что а'≠1, 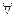 а
а 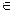 ℕ.
ℕ.
(Р2). Для любого натурального числа существует единственное натуральное число, непосредственно следующее за ним, т.е. 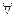 а
а 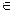 ℕ,
ℕ, 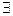 ! а'
! а' 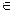 ℕ, т.е. из а=b => а'= b',
ℕ, т.е. из а=b => а'= b', 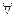 а,b
а,b 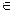 ℕ.
ℕ.
(Р3). Любое натуральное число непосредственно следует не более чем за одним натуральным числом, т.е. из а'= b' => а=b, 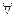 а,b
а,b 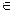 ℕ.
ℕ.
(Р4). Аксиома индукции. Пусть МÍℕ. Если 1 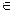 М и из а
М и из а 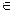 М всегда следует, что а'
М всегда следует, что а' 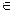 М, то М=ℕ.
М, то М=ℕ.
Замечание 1. Если а'= b, то элемент а называется предшествующим для элемента b.
Теорема 1. 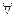 а
а 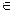 ℕ, а≠1, существует предшествующее натуральное число.
ℕ, а≠1, существует предшествующее натуральное число.
Лемма 1. 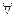 а,b
а,b 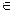 ℕ : из а'≠b' => а≠b.
ℕ : из а'≠b' => а≠b.
Лемма 2. 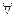 а,b
а,b 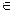 N: из а≠b => а'≠b'.
N: из а≠b => а'≠b'.
Теорема 2 (Евклид). Множество ℕ бесконечно.
Доказательство. Допустим, что ℕ – конечное множество. Рассмотрим последовательность натуральных чисел следующего вида: 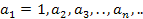 (1), где
(1), где 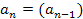 ', n=2,...,
', n=2,..., 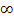 .
.
Так как ℕ - конечное множество, то в (1) не все элементы различны => 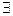 k, такое что (2)
k, такое что (2) 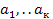 - попарно различные натуральные числа, а
- попарно различные натуральные числа, а 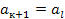 (3), 1
(3), 1 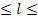 k. Так как
k. Так как 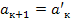 , то из (3) =>
, то из (3) => 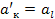 (5).
(5).
Покажем, что 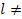 1. Действительно, так как по (Р1) а'≠1,
1. Действительно, так как по (Р1) а'≠1, 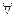 а
а 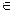 ℕ , то
ℕ , то 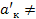 1 =>
1 => 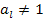 , т.е.
, т.е. 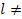 1 =>
1 => 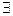
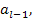 причем по (4)
причем по (4)  (6).
(6).
Из (5)-(6) => 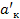 =
= 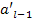 =>
=> 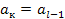 - противоречие с (2) => ℕ - бесконечное множество. Теорема доказана.
- противоречие с (2) => ℕ - бесконечное множество. Теорема доказана.
Различные формы метода математической индукции
Теорема 3 (I форма метода математической индукции). Если утверждение Т истинно при n=1 и из истинности утверждения Т для n=k следует истинность утверждения Т для n=k+1, то утверждение Т истинно 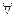 n
n 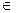 N.
N.
Доказательство. Пусть М – множество всех натуральных чисел, для которых Т истинно 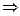 М
М 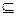 N. Так как по условию при n=1 Т истинно, то 1
N. Так как по условию при n=1 Т истинно, то 1 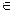 М.
М.
Пусть а 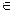 М
М 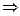 Т истинно при n=a
Т истинно при n=a 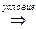 Т истинно при n=a+1=
Т истинно при n=a+1= 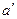
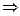
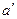
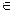 М. Таким образом, по (P4) M=N, т. е. Т – истинно,
М. Таким образом, по (P4) M=N, т. е. Т – истинно, 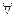 n
n 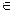 N.
N.
Теорема 4 (Обобщение II формы метода математической индукции). Если утверждение Т истинно при n=n0 и из истинности утверждения Т для n=k, k 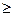 b, cледует истинность утверждения Т для n=k+1, то утверждение Т истинно
b, cледует истинность утверждения Т для n=k+1, то утверждение Т истинно 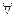 n
n 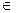 N , n
N , n 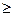 n0.
n0.
Теорема 5 (II форма метода математической индукции). Если утверждение Т истинно при n=1 и из истинности утверждения Т для любого натурального числа l<k следует истинность утверждения Т для k, то утверждение Т истинно 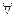 n
n 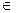 N.
N.
Теорема 6 (Обобщение II формы). Если утверждение Т истинно при n=n0 и из истинности утверждения Т для любого натурального числа l<k, l 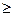 n0, следует истинность утверждения Т для k, то утверждение Т истинно
n0, следует истинность утверждения Т для k, то утверждение Т истинно 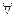 n
n 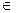 N, n
N, n 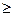 n0.
n0.