 |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
З а д а ч а 1. Бесконечная заряженная плоскость с поверхностной плотнос-тью заряда 6,00 нКл/м2 расположена перпендикулярно бесконечно длинной заряженной нити с линейной плотностью заряда -5,00 нКл/м. На биссектрисе угла между плоскостью и нитью на расстоянии 500 мм от вершины угла находится точечный заряд -10,0 нКл. Найти величину и направление напряженности электрического поля в точке, лежащей на биссектрисе этого угла и отстоящей от его вершины на расстоянии 100 мм; разность потенциалов электрического поля между двумя точками, расположенными на биссектрисе угла на расстоянии 100 и 300 мм от вершины.
| Дано: | СИ |
| ||||||||||||||||
| σ = 6,00 нКл/м2 |  Кл/м2 Кл/м2
| |||||||||||||||||
τ =  5,00 нКл/м 5,00 нКл/м
|  Кл/м Кл/м
| |||||||||||||||||
q =  10,0 нКл 10,0 нКл
|  Кл Кл
| |||||||||||||||||
| a = 100 мм | 0,1 м | |||||||||||||||||
| b = 300 мм | 0,3 м | |||||||||||||||||
| c = 500 мм | 0,5 м | |||||||||||||||||
| α = 45º | ||||||||||||||||||
 - ?
(φ1 – φ2) - ? - ?
(φ1 – φ2) - ?
|
 ,
,  ,
,  электрического поля, созданного плоскостью (
электрического поля, созданного плоскостью (  ), заряженной нитью (
), заряженной нитью (  ) и точечным зарядом (
) и точечным зарядом (  ). Результирующую напряженность
). Результирующую напряженность  в этой точке найдем по принципу суперпозиции электрических полей:
в этой точке найдем по принципу суперпозиции электрических полей:
 (1)
(1)
Для записи векторного уравнения (1) в скалярной форме выбираем инерциальную систему отсчета и находим проекции всех векторов на координатные оси:
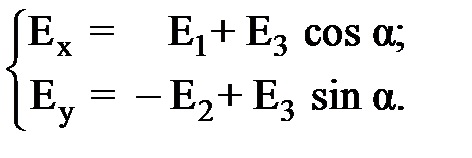 (2)
(2)
Значение напряженности полей, создаваемых каждым электрическим зарядом, вычислим по формулам:
для бесконечной заряженной плоскости -
 , (3)
, (3)
где  - электрическая постоянная (см. прил.);
- электрическая постоянная (см. прил.);
для бесконечно длинной заряженной нити –
 , (4)
, (4)
где  - кратчайшее расстояние от нити до точки 1;
- кратчайшее расстояние от нити до точки 1;
для точечного электрического заряда –
 . (5)
. (5)
С учетом формул (3) - (5) получим:
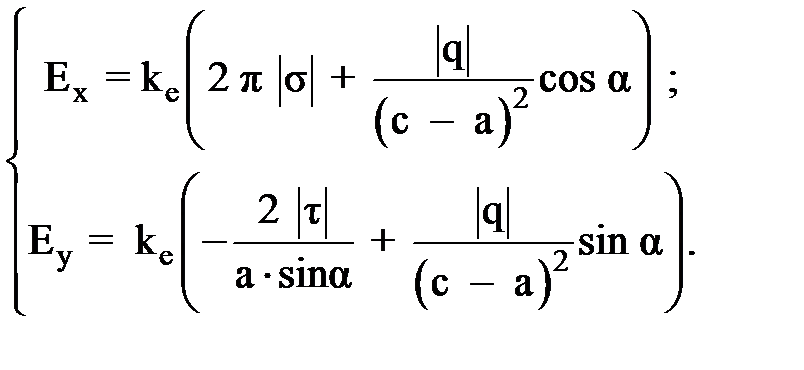 (6)
(6)
Проверяем единицы измерения:

Производим вычисления:


Величину напряженности в точке 1 найдем по формуле:
 (7)
(7)

Для вычисления разности потенциалов между точками 1 и 2 электри-ческого поля воспользуемся связью между разностью потенциалов поля и напряженностью этого поля
 (8)
(8)
и принципом суперпозиции электрических полей (потенциал результирующего электрического поля в точке равен алгебраической сумме потенциалов полей, создаваемых в этой точке отдельными зарядами).
Разность потенциалов между точками 1 и 2, создаваемая заряженной плоскостью, можно вычислить по формуле:
 (9)
(9)
где x1 и x2 – кратчайшее расстояние от плоскости до точек 1 и 2;

Разность потенциалов между точками 1 и 2, создаваемая заряженной нитью, рассчитывается по уравнению:
 (10)
(10)
где by и ay – кратчайшее расстояние от нити до точек 1 и 2; by = b sinα; ay = a sinα.
Разность потенциалов в точках 1 и 2, создаваемая точечным зарядом, вычисляется по выражению:
 (11)
(11)
где r1 и r2 – кратчайшее расстояние от точечного заряда до точек 1 и 2; r1 = c – a = = 0,4 (м); r2 = c – b = 0,2 (м).
Результирующая разность потенциалов  электрического поля между точками 1 и 2 в соответствии с принципом суперпозиции вычисляется по формуле:
электрического поля между точками 1 и 2 в соответствии с принципом суперпозиции вычисляется по формуле:
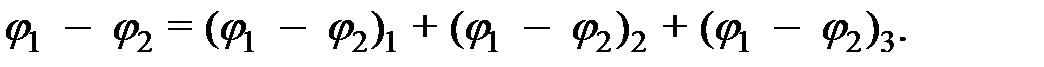 (12)
(12)
Из-за громоздкости формулы (12) проведем вычисления слагаемых по отдельности:
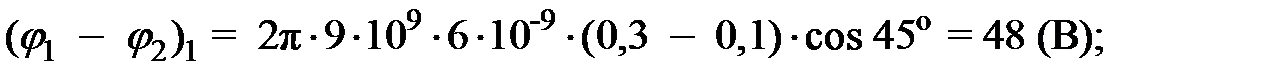
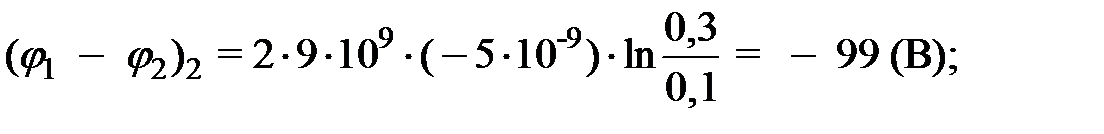

Окончательный результат:
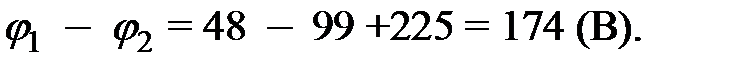
Ответ: 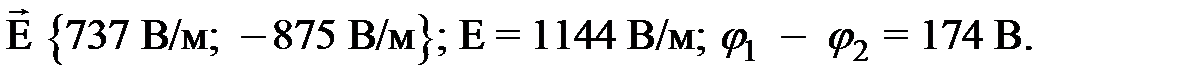
Задача 2. Два металлических шарика радиусом 10,0 и 50,0 мм заряжены: первый – до потенциала 600 В, а второй имеет заряд 3,00 нКл (рис. 2). Определить, насколько изменятся потенциалы шариков после их соединения.
| Дано: | СИ |
| |||||||
| R1 = 10 мм | 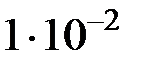 м м
| ||||||||
| R2 = 50 мм |  м м
| ||||||||
| φ1 = 600 В | |||||||||
| q2 = 3,00 нКл |  Кл Кл
| ||||||||
| ∆φ1 – ? ∆φ2 – ? |
Потенциал второго шарика до соединения вычисляют по формуле:
 (1)
(1)

Так как потенциалы шариков разные, то после их соединения начнется перезарядка, которая будет продолжаться до тех пор, пока потенциалы шариков не уравняются:
 (2)
(2)
Используя условие (2) и применяя закон сохранения электрического заряда, запишем:
 (3)
(3)
Решая систему (3), получим:
 (4)
(4)
Тогда, учитывая, что 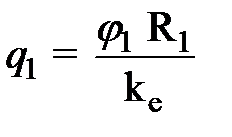 , запишем:
, запишем:
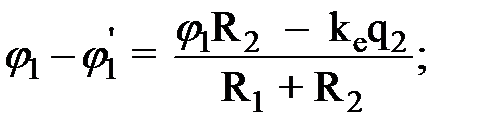 (5)
(5)
 (6)
(6)
Проверяем единицу измерения:

Производим вычисления:


Ответ: потенциал первого шарика уменьшится на 50 В, а второго – возрастет на 10 В.
Задача 3. В схеме на рис. 3 ЭДС E1 = 2,00 В; E2 = 1,50 В; E3 = 3,00 В; E 4 = 4,50 В. Внутренние сопротивления всех источников одинаковы и равны 0,5 Ом. Сопротивления резисторов: R1 = 1,00 Ом; R2 = 2,00 Ом; R3 = 3,00 Ом. Найти силу тока во всех участках цепи. Какое количество тепла выделяется в резисторе R2 за одну минуту?
| Дано: | Решение.
| |||||||||||||||||||||||
| E 1 = 2,00 В | ||||||||||||||||||||||||
| E 2 = 1,50 В | ||||||||||||||||||||||||
| E 3 = 3,00 В | ||||||||||||||||||||||||
| E 4 = 4,50 В | ||||||||||||||||||||||||
| r1 = r2 = r3 = r4 = 0,5 Ом | ||||||||||||||||||||||||
| R1 = 1,00 Ом | ||||||||||||||||||||||||
| R2 = 2,00 Ом | ||||||||||||||||||||||||
| R3 = 3,00 Ом | ||||||||||||||||||||||||
| t = 60 с | ||||||||||||||||||||||||
| I1 - ? I2 - ? I3 - ? Q2 - ? |
Так как электрическая цепь, приведенная на рис. 3, разветвленная, то для решения задачи нельзя использовать закон Ома для замкнутой цепи. Решаем задачу с помощью правил Кирхгофа.
Выбираем узел А, произвольно расставляем направление токов в подходящих к узлу проводах и записываем для него первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю (токи, подходящие к узлу, берем со знаком «плюс», отходящие – со знаком «минус»):
 (1)
(1)
Выбираем в цепи замкнутый контур – АВСА, указываем произвольно направление обхода контура и расставляем на источниках ЭДСстрелки, указывающие направление переноса заряда сторонними силами внутри источников (от «минуса» - к «плюсу»). Записываем для этого контура второе правило Кирхгофа: алгебраическая сумма снижения напряжения в замкнутом контуре равна алгебраической сумме ЭДС, действующих в этом контуре (если направление тока на сопротивлении совпадает с направлением обхода в контуре, то падение напряжения на этом сопротивлении имеет знак «плюс», если не совпадает – знак «минус»; если направление стрелки у ЭДС совпадает с направлением обхода контура, то перед ЭДС ставим знак «плюс», если противоположно – знак «минус»):
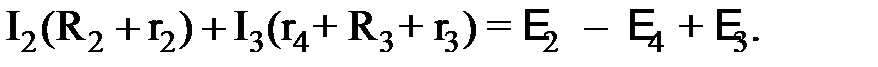 (2)
(2)
Выбираем другой замкнутый контур – ACDA – и аналогично записываем для него второе правило Кирхгофа:
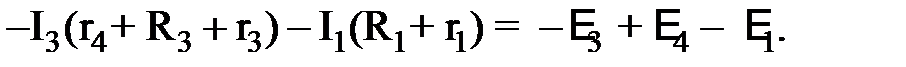 (3)
(3)
Для нахождения силы тока в участках цепи необходимо решить систему трех линейных уравнений:
 (4)
(4)
Решаем систему методом Крамера:
 (5)
(5)


Проверка по первому закону Кирхгофа:

Количество тепла, выделяемого при прохождении тока по проводнику R2, вычислим по закону Джоуля – Ленца:
 (6)
(6)

Ответ: I1 = 0,165 A; I2 = -0,101 A; I3 = 0,064 A; Q2 = 1,23 Дж.
Задача 4. По контуру в виде равностороннего треугольника со стороной 200 мм течет ток силой 15,0 А. Перпендикулярно плоскости контура проходят два бесконечно длинных прямых изолированных проводника, в которых протекают токи силой в 30,0 А в противоположных направлениях. Проводники проходят через две вершины треугольника. Найти величину и направление индукции магнитного поля в точке пересечения высот треугольника.
| Дано: | СИ | Решение.
  
| ||||||||||||||||
| a = 200 мм | 0,2 м | |||||||||||||||||
| I1 = 15,0 A | ||||||||||||||||||
| I2 = I3 = 30,0 A | ||||||||||||||||||

|
| r3 |
| r2 |
Магнитное поле создается замкнутым контуром, состоящим из трех проводников конечной длины, и двумя бесконечно длинными проводниками. Определяем с помощью «правила буравчика» направление индукции магнитного поля, создаваемого каждым проводником в центре треугольника (рис. 4) и на основании принципа суперпозиции магнитных полей записываем:
 (1)
(1)
где  ,
, 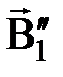 и
и  - магнитная индукция поля проводников конечной длины замкнутого контура с током I1;
- магнитная индукция поля проводников конечной длины замкнутого контура с током I1;
 и
и 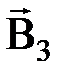 - магнитная индукция полей бесконечно длинных проводников с токами I2 и I3.
- магнитная индукция полей бесконечно длинных проводников с токами I2 и I3.
Для записи векторного уравнения (1) в скалярной форме выбираем удобную инерциальную систему отсчета (см. рис. 4, ось OZ – на нас) и находим проекции всех векторов на координатные оси:
 (2)
(2)
Магнитную индукцию поля, создаваемого каждой стороной треугольного контура, вычислим по формуле:
 (3)
(3)
где  - кратчайшее расстояние от проводника с током I1 до центра треугольника;
- кратчайшее расстояние от проводника с током I1 до центра треугольника;

Тогда
 (4)
(4)
Магнитную индукцию поля, создаваемого бесконечно длинными проводниками, вычислим по формулам:
 (5)
(5)
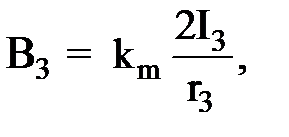 (6)
(6)
где r2 = r3 – радиус описанной окружности.
С учетом формул (5), (6) получим:
 (7)
(7)
 (8)
(8)
(так как I2 = I3 ).
Проверяем единицы измерения:

Производим вычисления:

Значение результирующей магнитной индукции поля в центре рассчитаем по формуле:
 (9)
(9)

Ответ: 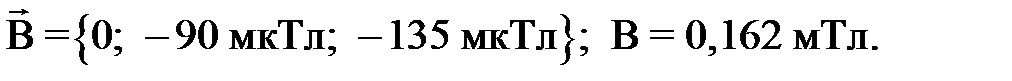
Задача 5. В однородном горизонтальном магнитном поле находится прямолинейный медный проводник с током 20,0 А, расположенный горизонтально и перпендикулярно полю. Какова должна быть магнитная индукция поля, чтобы проводник, имеющий поперечное сечение 2,00 мм2, находился в равновесии?
| Дано: | СИ |   
| |||||
| I = 20,0 A | |||||||
| S = 2,00 мм2 | 
| ||||||
| ρ = 8900 кг/м3 | |||||||
| В – ? |
На проводник с током (рис. 5) действует сила тяжести  (со стороны Земли) и сила Ампера
(со стороны Земли) и сила Ампера  (со стороны магнитного поля). Чтобы проводник находился в равновесии, сила
(со стороны магнитного поля). Чтобы проводник находился в равновесии, сила  должна быть направлена против
должна быть направлена против  и должна быть равной ей по величине:
и должна быть равной ей по величине:
 (1)
(1)
В проекции на ось ОУ имеем:
 (2)
(2)
где 
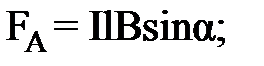
ρ - плотность материала проводника (медь);
V = Sl - объем проводника, находящегося в магнитном поле;
α = 90º - угол между направлениями магнитной индукции и тока в проводнике.
С учетом изложенного выше получим:
 (3)
(3)
Проверяем единицу измерения:

Производим вычисления:

Ответ: В = 8,7 мТл.
Задача 6. Рамка площадью 60,0 см2, имеющая 200 витков, равномерно вращается с частотой 5,00 об/с в однородном магнитном поле с индукцией 0,50 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Сопротивление витков рамки равно 12 Ом. Определить мгновенное значение ЭДС индукции, соответствующее углу поворота рамки в 30º, и максимальный ток, индуцируемый в рамке. В начальный момент времени плоскость рамки перпендикулярна магнитному полю.
| Дано: | СИ | Решение.


| |||
| N = 200 | |||||
| S = 60,0 см2 | 
| ||||
| ν = 5,00 об/с | |||||
| B = 0,5 Тл | |||||
| R = 12,0 Ом | |||||
| α1 = 30º | |||||
| Ei - ? Ii max - ? |
При вращении рамки в магнитном поле (рис. 6) меняется потокосцепление с рамкой, вследствие чего в рамке согласно явлению электромагнитной индукции индуцируется ЭДС индукции, мгновенное значение которой определяется по основному закону электромагнитной индукции (по закону Фарадея – Ленца):
 (1)
(1)
где N – число витков в рамке.
Магнитный поток через рамку
 (2)
(2)
При равномерном вращении рамки угол поворота рамки изменяется по закону:
 (3)
(3)
где  - циклическая (круговая) частота вращения, с-1;
- циклическая (круговая) частота вращения, с-1;
 - линейная частота вращения, об/с.
- линейная частота вращения, об/с.
С учетом уравнений (2) и (3) получим выражение для расчета ЭДС индукции:
 (4)
(4)
Проверяем единицу измерения:
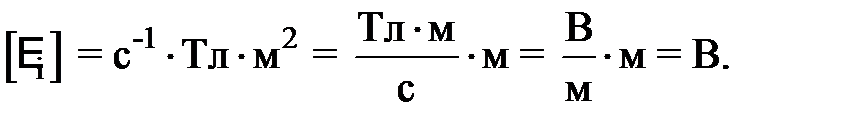
Вычисляем мгновенное значение ЭДС индукции, соответствующее углу поворота рамки α1 = 30º:
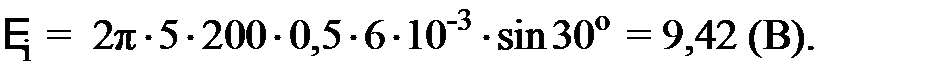
Величину индукционного тока в рамке можно найти, воспользовавшись
законом Ома:
 (5)
(5)
Максимальное значение Ii max будет соответствовать максимальному значению синуса:  , тогда
, тогда
 (6)
(6)
Производим вычисления:

Ответ: Ei = 9,42 В; Ii max = 1,57 А.
Задача 7. В идеальном колебательном контуре индуктивность катушки равна 100 мГн, а амплитуда колебаний силы тока в цепи – 20 А. Найти энергию электрического поля конденсатора и магнитного поля катушки в тот момент времени, когда мгновенное значение силы тока в два раза меньше амплитудного значения.
| Дано: | СИ | Решение.
Полная энергия идеального колебательного контура складывается из энергии электрического и магнитного полей:
 (1) (1)
|
| L = 100 мГн | 0,1 Гн | |
| I0 = 20 мА | 0,2 A | |
| i = I0/2 | ||
| We – ? Wm – ? |
В идеальном колебательном контуре отсутствует диссипация энергии, поэтому полную энергию можно вычислить через максимальные значения энергии электрического или магнитного поля:
 (2)
(2)
Энергия магнитного поля для момента времени, когда i = I0/2,
 (3)
(3)
Тогда энергия электрического поля конденсатора
 (4)
(4)
Производим вычисления:

Ответ: We = 15 мкДж; Wm = 5 мкДж.
З а д а ч а 8. Амплитуда затухающих колебаний математического маятника длиной 800 мм уменьшилась в два раза за 3 мин. Чему равна добротность этого осциллятора?
| Дано: | СИ | Решение.
Добротностью осциллятора называется увеличенное в 2π раз отношение энергии, первоначально запасенной осциллятором, к потерям энергии за один период:
 . (1) . (1)
|
| l = 800 мм | 0,8 м | |
| t1 = 3 мин | 180 с | |
| A0/A = 2 | ||
| t2 = T | ||
| Q – ? |
При затухающих колебаниях амплитуда и энергия убывают по законам:
 (2)
(2)
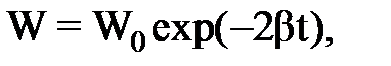 (3)
(3)
где β – коэффициент затухания осциллятора, который можно найти из соотно-шения:
 (4)
(4)

Тогда потеря энергии осциллятором за один период
 (5)
(5)
Период затухающих колебаний математического маятника
 (6)
(6)
а так как  <<
<<  , то это случай слабозатухающих колебаний.
, то это случай слабозатухающих колебаний.
Тогда окончательно имеем:
 (7)
(7)
Производим вычисления:

Ответ: Q = 458.
ТАБЛИЦА ВАРИАНТОВ И НОМЕРА ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ № 2
| Вариант | Номера задач | Вариант | Номера задач | ||||||||||||||
ЗАДАЧИ


