Главная | Обратная связь

ВЕКТОРНІ І СКАЛЯРНІ ВЕЛИЧИНИ. ДІЇ НАД ВЕКТОРАМИ

Механічний рух тіл. Основна задача механіки та її розв’язання. Фізичне тіло і матеріальна точка. Поступальний рух. Система відліку. Відносність механічного руху, векторні і скалярні величини. Дії над векторами.

Кінематикою називають розділ механіки, в якому рух тіл розглядається без з'ясування причин цього руху.

Для того щоб сказати, рухається тіло чи ні, необхідно подивитися, чи змінюється його положення відносно інших тіл.

Механічним рухом називають зміну положення тіла відносно інших тіл з часом.

Тіло, розмірами якого у даних умовах задачі можна знехтувати, називають матеріальною точкою. Наприклад, коли йдеться про рух космічного корабля, його розміри можна не враховувати порівняно з відстанню від Землі, корабель — матеріальна точка. А для космонавта, який знаходиться у космосі, корабель не є матеріальною точкою.

Положення тіла можна задати тільки відносно іншого тіла. Таке тіло називають тілом відліку. Тілом відліку може бути будь-яке тіло. Для визначення положення тіла у просторі користуються системою координат. Якщо тіло рухається, тобто його координати змінюються відносно тіла відліку, необхідним є прилад для вимірювання часу руху тіла.

Тіло відліку, система координат і прилад для вимірювання часу становлять систему відліку.

Нехай мат.т. рухається з положення 1 в положення 2.

Положення мат.т. в просторі задається за допомогою координат x,y,z або вектора r

Лінія по якій рухається мат.т. називається траекторією. Довжина лінії – це довжина шляху S або ΔS якщо малий шлях. Вектор проведений з 1-» 2 назив: переміщення (Δ )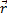

Будь-який механічний рух розглядається в системі відліку, обраній спостерігачем. У різних системах відліку тіло поводить себе по-різному. Наприклад, пасажир, який сидить у вагоні потягу, знаходиться у спокою відносно вагону і рухається відносно залізничних рейок.

Відносністю руху досить цікаво користуються для поповнення пальним баків літака у повітрі. Незважаючи на те, що відносно поверхні землі та атмосферного повітря літаки мчать зі швидкостями у кілька сотень кілометрів за годину, один відносно одного літаки перебувають у спокої.

У фізиці розглядають різні види руху:

· поступальний,

· коливальний,

· обертальний.

Рух тіла, при якому всі його точки рухаються однаково, називають поступальним рухом. Поступально рухається автомобіль на прямолінійній ділянці шляху, коливається маятник годинника, а стрілки годинника обертаються навколо нерухомої осі.

Коливаннями називають фізичні процеси, які точно чи майже точно повторюються через однакові проміжки часу.

Рух по будь-якій криволінійній траєкторії називається обертальним.

ВЕКТОРНІ І СКАЛЯРНІ ВЕЛИЧИНИ. ДІЇ НАД ВЕКТОРАМИ

Фізичні величини, що характеризують фізичну систему і її стани (наприклад взаємодію і механічний рух тіл) відображаються відповідними математичними об'єктами. Наприклад, щоб задати масу, температуру, об'єм тіла, треба визначити тільки їх числові значення у певних одиницях. Щоб задати силу або швидкість, треба обов'язково знати, крім числового значення, ще і їхній напрям у просторі, від чого залежить перебіг самого явища. Фізичні величини, які виражають тільки числом, називають скалярними, або скалярами.

Математичні дії зі скалярними величинами визначаються відомими вам правилами арифметики.
Фізичні величини, які характеризують числовим значенням, напрямом і геометричним способом додавання, називають векторними, або векторами. Числове значення вектора називають модулем вектора. Модуль вектора — величина скалярна и додатна. Векторну фізичну величину зображають стрілкою, довжина якої у вибраному масштабі дорівнює модулю вектора, а напрям збігається з напрямом фізичної величини (мал. 5). Якщо модуль вектора дорівнює нулю, то вектор зображається точкою.

Позначають вектори напівжирними літерами, наприклад а, b, с, або світлими літерами зі стрілками над ними: а, b, с.

Модуль вектора позначають або за допомогою математичного знака модуля | а |, | b |, | с |, або просто світлими літерами а, b, с. Надалі будемо користуватися цим останнім позначенням модуля вектора.
Вектори а і b є рівними, якщо вони мають однакові модулі і напрями (мал. 6). Вектори можна множити на скаляр, якщо помножити вектор а на скаляр к, то отримаємо вектор добутку р такого самого напряму, як у вектора а, з модулем, що дорівнює добутку модуля вектора а на модуль скаляра к: р = ка. Якщо вектор а помножити на (-1), то його модуль залишиться! таким самим, а напрям зміниться на протилежний. Якщо вектори а і Ь рівні за модулем і мають протилежні напрями, то їх називають протилежними і пишуть а = -b (мал. 7).

Математичні вектори можна переносити паралельно самим собі, з фізичними векторами це можна робити не завжди (наприклад, у задачах на рівновагу, коли дія важеля залежить від точки прикладання вектора сили).

Вектори можна додавати за правилами геометричного, або векторного, додавання. Якщо додати вектори а і b, то отримаємо вектор їхньої суми с, таку дію записують у вигляді векторної рівності: а + b = с. Щоб визначити напрям і довжину (модуль) вектора суми с користуються такими правилами. Правило аралелограма. Якщо вектори а і b мають спільний початок, то для їх додавання треба побудувати на цих векторах (як на сторонах) паралелограм (мал. 8), діагональ якого буде вектором суми векторів а і b. Якщо в цьому паралелограмі від кінця вектора а до кінця вектора b провести другу діагональ, то вона дорівнюватиме вектору різниці векторів а - b (перевірте це для вправи).

Якщо вектори а і b не мають спільного початку, то їх можна за допомогою паралельного перенесення привести до спільного початку. Правило трикутника. Паралельним перенесенням вектора b сумістити його початок з кінцем вектора а, тоді вектором суми с = а + b буде вектор, що з'єднує початок вектора а і кінець вектора b (мал. 9). Правило трикутника еквівалентне правилу паралелограма, але його зручно застосовувати, коли треба додавати декілька векторів. Також за цим правилом неважко отримати різницю векторів с = а + b .

Перепишемо цю рівність у вигляді с = а + (-b), бачимо, що віднімання вектора еквівалентне додаванню протилежного йому вектора (-b), що неважко зробити.
Коли вектори напрямлені вздовж однієї прямої або паралельні, їх називають колінеарними. Колінеарні вектори можуть бути напрямлені в один бік або в протилежні боки. Ви стикалися з обома випадками у 8 класі, коли визначали рівнодійну сил, прикладених до тіла, які діяли вздовж однієї прямої (мал. 10, а, б).
Колінеарні вектори додаються так само, як і неколінеарні, які ми розглядали вище. Задача у цьому разі значно спрощується, результат вам добре відомий: за модулем результуючий вектор дорівнює або арифметичній сумі (коли вектори напрямлені в один бік), або арифметичній різниці (коли вектори напрямлені протилежно) модулей векторів, що додаються. Результуючий вектор у першому випадку так само напрямлений, як і складові, у другому — у бік більшого за модулем вектора.
Рівняння механіки, як побачимо далі, мають зручну і наочну векторну форму, але під час обчислень ми оперуємо числами (скалярами), тому під час розв'язання задач виникає потреба перейти від векторного до скалярного запису. Для цього ознайомимося з поняттям проекції вектора на координатну вісь і правилами дій з проекціями векторів.

Вам добре відомо з геометрії поняття проекції точки на пряму (вісь). Проекцією точки на пряму (вісь) називають основу перпендикуляра, опущеного з цієї точки на пряму. Зрозуміло, що оскільки відрізок складається з послідовної і безперервної сукупності точок, то проекція відрізка на вісь складатиметься з проекцій усіх його точок на цю вісь, це буде відрізок на осі, обмежений проекціями початку і кінця даного відрізка.

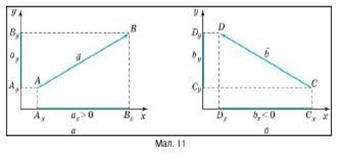
На мал. 11, а, б зображені вектори а і Ь, що по-різному орієнтовані відносно осей координат. Проекції точок і відрізків позначаються їхніми символами з нижнім індексом осі, проекція на яку розглядається. Наприклад, Ах, Сх — проекції початків векторів а і Ь на вісь Ох; Ву, Бу — проекції кінців векторів а і Ь на вісь Оу. Визначаючи проекцію вектора на вісь, треба враховувати, що знак проекції залежатиме від орієнтації цього вектора відносно осі. Проекцію вектора на вибрану вісь вважають додатною, якщо від проекції початку вектора до проекції його кінця треба рухатися у напрямі цієї осі. Проекцію вектора на вибрану вісь вважають від'ємною, якщо від проекції початку вектора до проекції його кінця треба рухатися у напрямі, протилежному напряму цієї осі.

Відповідно до цих правил, проекція вектора а на вісь Ох буде додатною, тобто ах > 0, а проекція вектора Ь на вісь Оу — від'ємною, тобто Ьх < 0. Обидві проекції цих векторів на вісь будуть додатними, тобто ах, Ьх > 0.

Якщо відомі проекції кількох векторів на певну вісь, то, користуючись наведеними правилами і правилами додавання векторів, неважко визначити проекцію суми векторів на цю вісь.
Проекція вектора суми векторів на певну вісь дорівнює сумі проекцій век-торів-доданків на цю вісь.
Якщо с = а + а, то сх = ах + Ьх, і су = ау + Ьу. Перевірте це самостійно. Ви бачите, що на площині векторному рівнянню відповідають два скалярних рівняння. Значення проекцій векторів залежать від їх розташування відносно системи координат, тому під час розв'язання задач намагаються вибирати напрями координатних осей таким чином, щоб спростити математичні перетворення й обчислення.
На мал. 12 показано різні випадки орієнтації вектора швидкості тіла V відносно осей координат. У загальному випадку вектор V напрямлений під кутом а до осі Ох (мал. 12, в) і його проекції визначатимуться за формулами тригонометрії: Vx = V сов а і Vу = V віп а. Якщо вектор V напрямлений паралельно осі Ох, то, як видно з мал. 12, а, модулі вектора і його проекції збігаються. При перпендикулярному розташуванні вектора V відносно осі

_____________________________________________________________

Скалярні та векторні величини
Фізичні величини, які використовують у фізиці для кількісної характеристики фізичних явищ і об'єктів, поділяються на два великі класи: скалярні величини і векторні величини.
До скалярних величин, або скалярів (від лат. зсаіагіз — східчастий), належать довжина, площа, температура, густина, робота й багато інших. Ці величини характеризуються одним значенням, і для їх позначення зазвичай використовують літери латинського та грецького алфавітів (І, і, р, А тощо). Наприклад, маса тіла — скалярна величина, і якщо ми говоримо, що маса тіла дорівнює двом кілограмам (т = 2 кг), то повністю визначаємо цю величину. Для визначення векторних величин важливо знати не тільки їхні значення, але й напрямки. Вектор (від лат. ьесіог — носій) — це напрямлений відрізок, тобто відрізок, що має і довжину, і напрямок. Довжина напрямленого відрізка називається модулем вектора. Позначають векторні величини літерами грецького та латинського алфавітів, над якими поставлено стрілки, або напівжирними літерами. Наприклад, швидкість записують так: V або V; модуль вектора швидкості відповідно позначають як V.
Правила додавання (віднімання) векторів відрізняються від правил додавання (віднімання) скалярних величин. Суму двох векторів визначають за допомогою правила паралелограма або правила трикутника (рис. 4.1, 4.2). Як визначити суму декількох векторів і різницю двох векторів, показано на рис. 4.3, 4.4.

У результаті множення векторної величини а на скалярну величину к виходить вектор с (рис. 4.5).
Зверніть увагу: у фізиці модулі векторної та скалярної величин мають — крім числових значень — ще й одиниці, у яких вони вимірюються. Одиниця їхнього добутку визначається як добуток одиниці векторної величини на одиницю скалярної. Припустимо, потрібно знайти переміщення літака, який протягом 0,5 год летить на північ зі сталою швидкістю 500 км/год. Вектор переміщення: 8 = VI. Оскільки і > 0, то вектор переміщення 8 буде напрямлений у той самий бік, що й вектор швидкості V, а модуль вектора переміщення дорівнюватиме: 8 = Vі = 500 км/год• 0,5 год = 250 км.
Як знайти проекції вектора на осі координат
З векторами здійснювати математичні а операції набагато складніше, ніж зі скалярами, тому в ході розв'язування задач від векторних фізичних величин переходять до їхніх проекцій на осі координат.
Нехай вектор а лежить в одній площині з осями ОХ і ОУ (рис. 4.6). Опустимо з точки А (початок вектора а) і точки В (кінець вектора а) перпендикуляри на вісь ОХ. Основи
цих перпендикулярів — точки А1 і зивають проекціями точок А і В на вісь ОХ, а відрізок А1В1 — проекцією вектора а на вісь ОХ. Проекцію вектора позначають тією самою літерою, що й вектор, із зазначенням у підіндексі осі, наприклад: ах. Якщо із кінців вектора а побудувати перпендикуляри до осі ОУ, дістанемо відрізок А2В2 — проекцію вектора а на вісь ОУ (ау).

Проекція вектора — величина скалярна, а її знак залежить від напрямків вектора й осі координат. Проекція вектора на вісь координат вважається додатною, якщо від проекції початку вектора до проекції його кінця треба рухатися в напрямку осі координат (див. рис. 4.6); проекція вектора вважається від'ємною, якщо від проекції початку вектора до проекції кінця вектора треба рухатися проти напрямку осі координат.

У загальному випадку проекцію вектора визначають звичайними геометричними методами (рис. 4.7, а). На практиці часто доводиться мати справу з випадками, коли вектор паралельний осі координат або перпендикулярний до неї. Якщо вектор паралельний осі координат, а його напрямок збігається з напрямком осі, то його проекція на цю вісь додатна й дорівнює модулю вектора (рис. 4.7, б). Якщо напрямок вектора протилежний напрямку осі координат, то його проекція на цю вісь дорівнює модулю вектора, взятому з протилежним знаком (рис. 4.7, в).

Якщо ж вектор перпендикулярний до осі координат, то його проекція на цю вісь дорівнює нулю (рис. 4.7, г). Дуже важливою властивістю проекцій є те, що проекція суми двох або декількох векторів на координатну вісь дорівнює алгебраїчній сумі проекцій цих векторів на дану вісь (рис. 4.8). Саме ця властивість дозволяє замінювати в рівнянні векторні величини їхніми проекціями — скалярними величинами — і далі розв'язувати одержане рівняння звичайним алгебраїчним методом.