Главная | Обратная связь

ДОДАВАННЯ ВЕКТОРНИХ ВЕЛИЧИН

У фізиці використовують багато векторних величин. Такими величинами є, наприклад, переміщення, швидкість, сила. Розглядаючи багато задач, треба вміти виконувати різні дії з векторними величинами. Розглянемо тут додавання векторних величин на прикладі додавання переміщень.
Нехай літак перелетів з міста М до міста Н, а звідти — до міста К. На рисунку 1.12, а вектором ^ позначено переміщення літака з М у Н, а вектором з2 — переміщення літака з Н у К. Результатом двох переміщень є переміщення 5 — це вектор, що з'єднує М і К.\

Ми виконали зараз додавання векторів за «правилом трикутника».

Щоб за цим правилом знайти суму двох векторів, треба початок другого вектора з'єднати з кінцем першого вектора (рис. 1.12, а). Тоді сумою цих двох векторів є вектор, початок якого збігається з початком першого вектора, а кінець — з кінцем другого вектора (рис. 1.12, б).

За допомогою «правила трикутника» можна додавати також вектори, напрямлені уздовж однієї прямої (рис. 1.12, в, г). Щоправда, у цьому випадку справжній трикутник не виходить, бо всі вектори лежать на одній прямій. Зверніть увагу: у цьому випадку рівність S = SХ + S2 має місце тільки тоді, коли вектори-доданки напрямлені однаково (рис. 1.12, в). Якщо ж вектори-доданки напрямлені протилежно, то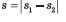

Скалярні і векторні величини

Скалярні і векторні величини. У фізиці використовуються як скалярні величини так і векторні.
Скалярна величина (скаляр) - величина, значення якої задається дійсним числом.
У механіці це: маса т, робота А, потужність У, енергія Е та інші. Скалярні величини можуть бути додатними або від'ємними. Сума скалярних величин обчислюється алгебраїчною сумою їх числових значень.

Векторна величина (вектор) - величина, значення якої задається дійсним числом і напрямком.
Модуль вектора - завжди додатний скаляр.

Дії над векторами. Над векторними величинами можна виконувати математичні дії додавання, віднімання, множення.

Сума векторних величин обчислюється геометричною сумою векторів, результуюча якої є також вектором.

Додають вектори, застосовуючи правило трикутника або правило паралелограма.
Правило трикутника: при додаванні векторів а і Ь вектори паралельним переміщенням розташовують так, щоб початок вектора Ь виходив із кінця вектора а, тоді вектор с, який виходить із початку вектора а і кінець якого збігається з кінцем вектора Ь і є сумарним вектором (мал. 2).
За правилом трикутника зручно додавати велику кількість векторів (мал. 3).

Правило паралелограма: два вектори а і Ь паралельним перенесенням розміщують так, що їх початки збігалися. Вважаючи, що обидва вектори є двома сторонами паралелограма, необхідно добудувати паралелограм. Тоді діагональ паралелограма, яка виходить із точки, де починаються вектори, і є сумарним вектором с (мал. 4). Числове значення сумарного вектора визначають за формулою

Числове значення різниці векторів визначають за формулою с = уіа2 + Ь2 - 2аЬ соз а , де а - кут між векторами а і Ь, що виходять з однієї точки (мал. 5). Так, як і у випадку дійсних чисел, віднімання векторів можна звести до їх додавання . Рі зницю векторів а і Ь можна визначити че ез суму вектора а з вектором (-Ь) (який за модулем дорівнює вектору Ь, але протилежний йому за напрямом), тобт о с = а - ь = а + (-Ь) (мал. 6). У випадку взаєм-ноперпендикуляр-них векторів а і Ь числові значення суми та різниці однакові. Сумарний вектор і вектор різниці відрізняються напрямками. При множенні вектора а на додатний скаляр к отримуємо новий вектор ка, напрям якого збігається з напрямом вектора а, а числове значення в к разів більше.

При множенні вектора а на від'ємний скаляр к отримуємо новий вектор ка, напрям якого протилежний напряму вектора а, а числове значення в к разів більше.
Скалярним добутком векторів а і Ь є скаляр с, що дорі внює добутку модулів векторів а і Ь, помножений на косинус кута між ними: с = (а • Ь) = а • Ь • соза .
Векторним добутком векторів а і Ь є вектор с, що дорівнює добутку модулів векторів і , омножений на синус кута між ними: с = [а х Ь] = а • Ь • зіпа.
Вектор с за модулем дорівнює пл ощі паралелограма, побудованого на векторах а і Ь, та направлений перп енд икулярно до площини, у якій лежать вектори а і Ь. До того ж, якщо спостерігати з кін -ця вектора с за обертанням вектора а до вектора Ь (у напрямку меншого кута), то воно відбувається проти годинникової стрілки (мал. 7). Проекція вектора на вісь. Будь-який вектор можна розкласти на складові, зокрема, за осями декартової системи координат.

Проекція вектора - відрізок, який отримують шляхом проектування вектора на відповідну числову вісь. Проекцією вектора а на вісь X називається величина а , яка визначається ах = а • созф, де а - модуль вектора, ф - кут між напрямом вектора та віссю X (мал. 8). Проекції вектора - величини скалярні. Проекція вектора на вісь буде додатною, якщо кут ф гострий, і від'ємною, якщо кут ф тупий, і нульовою, якщо ф прямий (вектор перпендикулярний до осі).

Проекція суми векторів на координатну вісь дорівнює алгебраїчній сумі проекцій векторів, що додаються (мал. 9).
Отже, векторні величини додаються геометрично, а скалярні -алгебраїчно.
Якщо (мал. 10) початком вектора а на координатній площині є точка А, координати якої (х1; у1), а кінцем вектора є точка В з координатами (х2; у2), то координатами (а1; а2) вектора а є числа а1 = (х - х1) та а2 = (У2 - Уі).

З формули відстані між двома точками випливає, що модуль вектора визначається: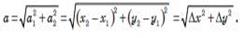