 |
|
Глава 2 Общие понятия о распределении случайных величин.
2.1 Представления эмпирических распределений.
Одним из самых простых преобразований статистических данных является их упорядочение по величине. Пусть (х1, ..., хn) - выборка объемаn из генеральной совокупностиX. Ее можно упорядочить, расположив значения в неубывающем порядке, образуя «вариационный ряд»:
x(1) ≤ x(2) ≤…≤ x(i)≤… ≤ x(n) (2.1)
где x(1)- наименьший, x(n)- наибольший из элементов выборки.
x(i)(иногда обозначают Z(i))соответственно - члены вариационного ряда.
Распределение случайной величины на шкале подчиняется определённым законам, может, например, концентрироваться в центре интервала шкалы или наоборот, рассеиваться равномерно в пределах некого интервала. От распределения случайной величины зависит способ обращения с ней, способ её оценки.
Наиболее простой характеристикой распределения и одновременно способом упорядочения случайной величины является статистический ряд. Это таблица, которая в первой строке содержит значения Z(i), а во второй - числа их повторений (табл. 2.1). Число niназывают частотой,а отношение ni/n- относительной частотой.
Таблица 2.1Статистический ряд
| Z(1) | Z(2) | … | Z(m) |
| n1 | n2 | … | nm |
Статистические данные,представленные в виде статистического ряда, называют группированными.
Разновидностьстатистического ряда -интервальный статистический ряд (таблица 2.2).В интервальном статистическом ряде исходные данные группируют следующим образом: отрезок J, содержащий все выборочные значения, разбивают на mпромежутков Ji, как правило, одинаковой длины. При этом считают, что каждый промежуток содержит своё левое граничное значение, но лишь последний промежуток содержит и своё правое граничное значение.
Таблица 2.2Интервальный статистический ряд
| J1 | J2 | … | Jm | J |
| n1 | n2 | … | nm | 
|
Иногда в верхней строке табл. 1.2 указывают не интервал, а его середину, а в нижней строке вместо частоты записывают относительную частоту. Число промежутков m, на которые разбивают отрезок J, выбирают в зависимости от объема выборки n одним из следующих способов:
- по формуле Стержеса: m = 1 + 3,32·lg n;
- с помощью таблицы 2.3.
Таблица 2.3 Выбор числа интервалов вариационного ряда
| Объем выборки, n | 25-40 | 40-60 | 60-100 | 100-200 | Больше 200 |
| Число интервалов, m | 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
- по формуле  (2.2)
(2.2)
Статистический или интервальный ряд можно представить графиком, называемым гистограммой (рис. 2.1), составленным из прямоугольников с высотами niили ni/n. Нетрудно увидеть, что в последнем случае суммарная площадь всех прямоугольников, образующих такую диаграмму, равна 1:
 (2.3)
(2.3)

Рис. 2.1.Гистограмма случайной величины X
Наряду с гистограммой часто для приближенного описания функции р(х) используют другое графическое представление, которое называют «полигоном частот». Это ломаная линия, отрезки которой соединяют середины горизонтальных отрезков, образующих прямоугольники в гистограмме (рис. 2.2).
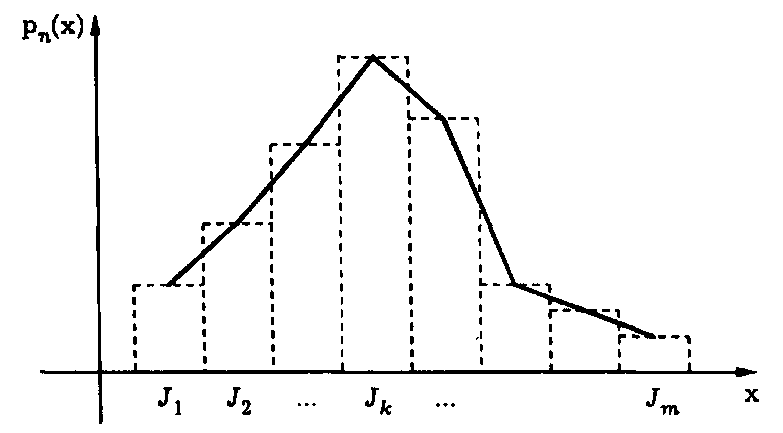
Рис. 2.2. Гистограмма (пунктир)и полигон частот эмпирическойфункциираспределения
2.2 Плотность и интегральная функция распределения
По виду гистограммы или полигона частот можно судить о характере плотности рассеяния случайной величины X. Например, по распределениям, представленным на рис. 1.1 и 1.2, видно, что плотность распределениямаксимальна в середине рассматриваемого интервала шкалы x и минимальна по краям.
Эмпирической плотностью распределения называют функцию, которая во всех точках интервала Jпринимает значение относительных частот, а вне интервала Jравна нулю (2.4).
 (2.4)
(2.4)
Если длина промежутков Jk достаточно мала и объем выборки n велик, то с вероятностью, близкой к 1, можно утверждать, что величина ni/nявляется статистическим аналогом плотности распределения непрерывной случайной величины X (рис. 2.3).

Рис. 2.3. Графики плотности распределения дискретной и непрерывной случайных величин (D - наибольшее возможное значение дискретной величины d, Xmin, Xmax - пределы, за которыми f(x)=0.
Эмпирической (интегральной) функцией распределенияназывают скалярную функцию Fn(x), которая определена следующим образом:
 (2.5)
(2.5)
где n- объем всей выборки, n(x) - "накопленный объем" для интервала (xmin - x). Иначе говоря, она определяет вероятность того, что случайная величина меньше или равна x.При этом для дискретного распределения функция Fn(x)кусочно-постоянна и изменяется скачками в каждой точке перехода к следующему интервалу. На рис. 2.4 показано, что величина каждого очередного «скачка» равна относительной частоте соответствующего интервала.

Рис. 2.4. График интегральной функции дискретного распределения
На рис. 2.5 показано в сравнении принципиальное различие интегральной функции Fn(x) дискретного и непрерывного распределения: в отличие от дискретного при непрерывном распределении Fn(x) увеличивается непрерывно, достигая 1 (единицы) при максимальном значении x.

Рис. 2.5 Графики интегральных функций дискретного и непрерывного распределения в сравнении.
Для наглядного представления о связи плотности f(x) и интегральной функции F(x), они приведены совместно для произвольного распределения на рис. 2.6. Можно наблюдать, что F(x) представляет собой площадь под кривой f(x) в интервале от -∞ до значения xi. Такимобразом, интегральная функция F(x) в интервале значений х1 и х2(иначе - вероятность попадания величины xв интервал значений от х1 до х2{х1<X< х2})равна разнице площадейF(x2) - F(x1), то есть заштрихованной площади под f(x)между х1и х2(см. рис. 2.6.).

Рис. 2.6. Плотность (f) и функция (F) произвольного распределения непрерывной случайной величины.