 |
|
СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Нехай задано систему лінійних рівнянь

в якій коефіцієнти  і вільні члени
і вільні члени  відомі, а
відомі, а  – невідомі. Розв’язати систему– це означає знайти впорядковану сукупність чисел
– невідомі. Розв’язати систему– це означає знайти впорядковану сукупність чисел  таку, що при заміні
таку, що при заміні  відповідно на
відповідно на  кожне рівняння перетворюється на тотожність.
кожне рівняння перетворюється на тотожність.
Систему рівнянь можна записати у векторній формі. Для цього введемо у просторі, розмірність якого дорівнює числу рівнянь, вектори
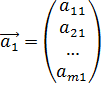 ,
,  , …,
, …, 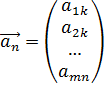 ,
,  .
.
Тоді система набере вигляду

Згідно з цим рівнянням розв’язання системи можна звести до встановлення лінійної залежності системи векторів  ,
,  , …,
, …,  і
і  . Так, система не має розв’язку, коли вектори
. Так, система не має розв’язку, коли вектори  ,
,  , …,
, …,  лінійно незалежні.
лінійно незалежні.
Введемо матрицю коефіцієнтів системи векторів, матрицю-стовпець правої частини, матрицю-стовпець невідомих
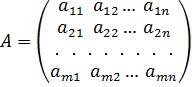 ,
,  ,
, 
Використовуючи означення добутку матриць, систему можна записати у вигляді 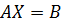 . Ця форма запису системи називається матричною.
. Ця форма запису системи називається матричною.
Поставивши задачу про відшукання розв’язку системи, ми не задавали ніяких обмежень ні на число рівнянь, ні на число невідомих.
Тому система може не мати розв’язку.
Наприклад,

Система може мати нескінченну множину розв’язків.
Наприклад,
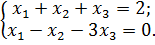
Для цієї системи впорядкована трійка чисел 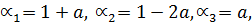
де a (будь-яке дійсне число) є розв’язком.
Система може мати також єдиний розв’язок.
Наприклад,

Розв’язком цієї системи є тільки одна впорядкована пара чисел (2; 1).
Система лінійних рівнянь називається сумісною, якщо вона має розв’язок, і несумісною, якщо не має розв’язків.
Перед тим як встановити умову сумісності системи лінійних рівнянь, введемо деякі поняття. Матриця А коефіцієнтів при невідомих системи називається основною.
Приєднаємо до матриці А стовпець вільних членів. Дістанемо так звану розширену матрицю А* даної системи:
 .
.
Теорема Кронекера – Капеллі (умова сумісності системи лінійних рівнянь). Система сумісна тоді і тільки тоді, коли ранг основної матриці дорівнює рангу розширеної матриці: 
Д о в е д е н н я. Якщо система має розв’язок  , то вектор
, то вектор  є лінійною комбінацією векторів
є лінійною комбінацією векторів  ,
,  , …,
, …,  , тобто стовпчик із вільних членів матриці є лінійною комбінацією стовпців матриці А системи. Базисні мінори матриць А і А* не змінювались:
, тобто стовпчик із вільних членів матриці є лінійною комбінацією стовпців матриці А системи. Базисні мінори матриць А і А* не змінювались:  . Якщо
. Якщо  , то базисні мінори обох матриць збігаються, і згідно з теоремою про базисний мінор справедливе рівняння
, то базисні мінори обох матриць збігаються, і згідно з теоремою про базисний мінор справедливе рівняння  , тобто система має розв’язок.
, тобто система має розв’язок.
Метод Гаусса
Нехай дано систему m лінійних рівнянь з n невідомими

Серед цих рівнянь можуть бути такі, що 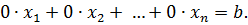
Далі вважатимемо, що система має розв’язок, тобто сумісна.
Якщо  , то рівняння
, то рівняння  не задовольняє ніякі значення
не задовольняє ніякі значення  . У цьому разі система не має розв’язку, вона несумісна.
. У цьому разі система не має розв’язку, вона несумісна.
Якщо  , то це рівняння задовольняють будь-які значення
, то це рівняння задовольняють будь-які значення  .
.
При цьому вираз називають не рівнянням, а тотожністю і записують  . Тотожність можна вилучити із системи. При цьому решта рівнянь матиме ті самі розв’язки, що і раніше. Говорять, що системи з тотожністю і без тотожності рівносильні. Дві системи лінійних рівнянь називаються рівносильними, якщо вони мають однакові розв’язки.
. Тотожність можна вилучити із системи. При цьому решта рівнянь матиме ті самі розв’язки, що і раніше. Говорять, що системи з тотожністю і без тотожності рівносильні. Дві системи лінійних рівнянь називаються рівносильними, якщо вони мають однакові розв’язки.
Над системами лінійних рівнянь виконують операції, які називаються елементарними:
а) додавання до обох частин рівняння відповідних частин іншого рівняння, помножених на деяке число λ;
б) перестановку рівнянь у системі;
в) вилучення із системи тотожності  ;
;
г) множення якого-небудь рівняння системи на дійсне число, відмінне від нуля;
д) перенумерування як рівнянь, так і невідомих.
Ці операції не порушують рівносильності системи рівнянь.
За допомогою операції (а) можна вилучити будь-яке невідоме з усіх рівнянь системи, окрім одного. При цьому невідоме, яке вилучають, називається провідним невідомим; коефіцієнти при провідному невідомому називаються провідними елементами, а рівняння, у якому зберігається провідне невідоме, називається провідним рівнянням.
Як приклад вилучимо з (m-1)-го рівняння системи (6.1) невідоме x1 і приймемо за головне перше рівняння. Для цього помножимо рівняння, з якого вилучимо x1, на λk, де k=2, 3, …, m, і додамо знайдене рівняння до головного. У результаті цього маємо 
Поклавши  , або
, або 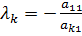 , дістанемо рівняння, в якому відсутнє невідоме x1. Аналогічно вилучимо з усіх рівнянь x1, крім головного (першого) рівняння. Потім, взявши за головне рівняння знайденої системи, вилучимо x2 з усіх наступних рівнянь і т. д. У результаті цього дістанемо так звану ступінчату систему
, дістанемо рівняння, в якому відсутнє невідоме x1. Аналогічно вилучимо з усіх рівнянь x1, крім головного (першого) рівняння. Потім, взявши за головне рівняння знайденої системи, вилучимо x2 з усіх наступних рівнянь і т. д. У результаті цього дістанемо так звану ступінчату систему

або систему у трикутній формі

Друга система має єдиний розв’язок, а перша система при r<n має n-r так званих вільних змінних, тобто невідомих, які набувають довільних значень.
Розглянута методика перетворення систем, називається методом послідовних вилучень невідомих Жордана – Гаусса, або, коротко, методом Гаусса.
Цей метод можна використовувати і для визначення сумісності системи. У цьому разі в результаті послідовного вилучення невідомих дійдемо системи, в якій деякі рівняння матимуть вигляд

Якщо в останніх рівностях хоча б одне з чисел dk, k=r+1, r+2, …, m не дорівнює нулю, то початкова система несумісна.
Таким чином, методом Гаусса можна відшукати розв’язок будь-якої системи без попереднього визначення її сумісності.
Приклади 6.1. Розв’язати методом Гаусса систему

Р о з в ’ я з а н н я. Випишемо розширену матрицю системи:
 . Застосуємо до неї метод Гаусса елементарних перетворень:
. Застосуємо до неї метод Гаусса елементарних перетворень:
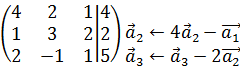


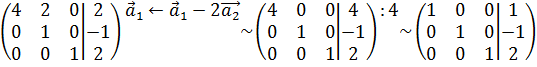
Таким чином: 
Приклад 6.2. Показати, що система несумісна.

Р о з в ‘ я з а н н я. Випишемо розширену матрицю системи:
 . Застосуємо до неї метод Гаусса елементарних перетворень:
. Застосуємо до неї метод Гаусса елементарних перетворень:
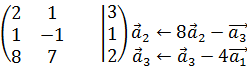
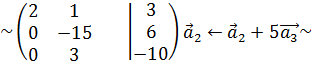
 -отримали, що 0=-44, це означає, що система розв’язків не має.
-отримали, що 0=-44, це означає, що система розв’язків не має.
Відповідь. Система не сумісна.