 |
|
Найбільше і найменше значення функції на відрізку
 Нехай функціянеперервна на відрізку
Нехай функціянеперервна на відрізку 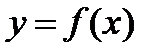 . Як відомо, така функція досягає своїх найбільшого і найменшого значень. Ці значення функція може прийняти або у внутрішній точці
. Як відомо, така функція досягає своїх найбільшого і найменшого значень. Ці значення функція може прийняти або у внутрішній точці 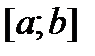 відрізка
відрізка  , або на межі відрізка, тобто при
, або на межі відрізка, тобто при  або
або 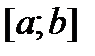 Якщо,
Якщо,  то точку
то точку  слід шукати серед критичних точок даної функції (див. Рис. 152).
слід шукати серед критичних точок даної функції (див. Рис. 152).
Рис. 152
Одержуємо наступне правило знаходження найбільшого і якнайменшого значень функції на :
знайти критичні точки на інтервалі ;
обчисли значення функції в знайдених критичних точках ;
1) обчислити значення функції на кінцях відрізка, тобто в точках і ;
2) серед всіх обчислених значень функції вибрати найбільше і якнайменше.
Зауваження: 1. Якщо функція на відрізку має лише одну критичну крапку і вона є точкою максимуму (мінімуму), то в цій точці функція приймає найбільше (якнайменше) значення. На малюнку 152 (нб– найбільше, max– максимальне ).
2. якщо функція на відрізку не має критичних крапок, то це означає, сто на ньому функція монотонно зростає або убуває. Отже, своє найбільше значення (М) функція приймає на одному кінці відрізка, а якнайменше (т)– на іншому.
Приклад 7.1.10. Знайти найбільше і якнайменше значення функції
 на відрізку
на відрізку  .
.
○ Знаходимо критичні точки даної функції:

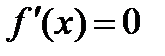 при
при  і при
і при  . Знаходимо
. Знаходимо  ,
,  ,
,  ,
, 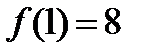 . Отже
. Отже  , в точці
, в точці 
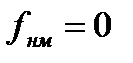 в точці
в точці 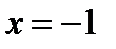 .
.
Знаходження найбільшого і найменшого значення функції широко застосовується при рішенні багатьох задач математики, фізики, хімії, економіки і інших дисциплін.
Практичні задачі: транспортна задача про перевезення вантажу з мінімальними витратами, задача об організації виробничого процесу з метою отримання максимального прибутку і інші задачі, пов'язані з пошуком оптимального розв’язання, приводять до розвитку і удосконалення методів відшукання найбільших і якнайменших значень. Розв’язанням таких задач займається особлива гілка математики – лінійне програмування.
Розглянемо більш просту задачу.●
Приклад 7.1.11. З кулі радіусу R виточити циліндр найбільшого об'єму. Які його розміри?
 ○ Позначимо через х і у висоту і діаметр циліндра. Тоді, як видно з малюнка 153,, а тому об'єм циліндра.
○ Позначимо через х і у висоту і діаметр циліндра. Тоді, як видно з малюнка 153,, а тому об'єм циліндра.
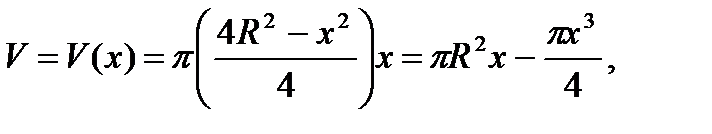
де .
Рис. 153.
Знаходимо найбільше і найменше значення функції на проміжку . Оскільки то при крім того . Тому – точка максимуму. Оскільки функція має одну критичну крапку, то циліндр будить має найбільший об'єм (рівний) при ; діаметр підстав циліндра рівний

Таким чином, шуканий циліндр має висоту, рівну, діаметр, рівний 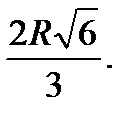 ●
●