Главная | Обратная связь

Теорема (про існування і неперервність оберненої функції).

Якщо функція 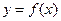монотонно зростаюча (спадна) і неперервна на відрізку , то на відрізку існує обернена функція , яка монотонно зростаюча (спадна) і неперервна на цьому відрізку.

Доведення.Розглянемо випадок монотонно зростаючої функції, поскільки другий випадок розглядається аналогічно.

Із останньої теореми 6 попереднього пункту, що слідує з ІІ теореми Вейєрштрасса, випливає, що . Поскільки функція на і є її множиною значень, то як слідує із вищесказаного, вона оборотна, а значить, на останньому відрізку обернена функція .

Покажемо тепер. що ця функція є 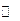на . Для цього візьмемо , причому, 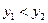. Доведемо, що . Очевидно, що 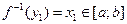, , причому, 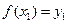, (за означенням). Таким чином, монотонність буде доведено, якщо ми покажемо, що . Припустимо, що останнє несправедливе, тобто . Звідси із монотонності функції на одержим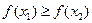о , або , а це протирічить нерівності, що 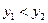. Значить, наше припущення невірне, а тому і на .

Доведемо тепер неперервність на . Користуватимемось при цьому означенням неперервності за Гейне.

Візьмемо для цього і доведемо, що неперервна в цій точці. Якщо це буде зроблено. то в силу довільності вибору із вказаного відрізка випливатиме неперервність оберненої функції на всьому відрізку.

Візьмемо 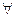послідовність . Розглянемо далі послідовність , яка 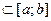. Поскільки , то 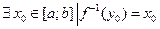. Неперервність функції в точці буде доведена, якщо буде встановлено, що , або що те саме , де .

Припустимо, що не збігається до , коли 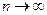. Звідси слідує, що 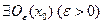, поза яким лежатиме нескінченна кількість членів послідовності . Позначимо всі ці члени даної послідовності, які лежать поза цим околом через 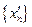. Значить, 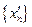є підпослідовність послідовності . Поскільки всі члени 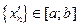то ця послідовність є обмежена. Значить, за теоремою Больцано-Вейєрштрасса з неї можна виділити збіжну підпослідовність . Нехай, 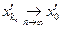. Зрозуміло, що 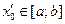і (тому, що всі члени послідовності лежать поза цим околом. а значить. і границя цієї послідовності не належить цьому околу). А це означає, що .

Розглянемо 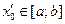. Поскільки за умовою неперервна на . то вона буде неперервною і в т. , а за означенням за Гейне з того, що 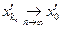, випливає, що . Звідси і з того, що є підпослідовністю , а остання співпадає з послідовністю 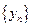, яка є збіжною, одержуємо, що , але за умовою . З теореми про єдність границі будемо мати, що , що неможливо, бо функція є монотонно зростаюча і .

Одержане протиріччя показує, що наше припущення про те. що неправильне. А значить. теорема доведена.