Главная | Обратная связь

К ВЫПОЛНЕНИЮ Заданий 1-2.

В результате статистического наблюдения получают массу данных по каждой единице изучаемой совокупности.

Для выявления закономерностей, присущих анализируемой совокупности единиц, необходимо систематизировать результаты статистического наблюдения и рассчитать обобщающие показатели: средние, показатели вариации, динамики, корреляции.

Средними величинами в статистике называют обобщающие показатели, выражающие типичные, характерные для определенных условий места и времени размеры и количественные соотношения явлений общественной жизни.

В статистике различают несколько видов средних величин, а именно: арифметическую, гармоническую, геометрическую и др.

В зависимости от частоты повторения вариант средние исчисляются как простые не взвешенные, так и взвешенные.

Среднюю арифметическую не взвешенную рассчитывают по формуле:

,

а среднюю арифметическую взвешенную –

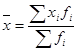
где - значение осредняемого признака,

- частота,

n- число единиц совокупности.

Средняя гармоническая не взвешенная определяется по формуле

,

а средняя гармоническая взвешенная -

 

,

где - сумма значений осредняемого признака по группе.

Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчёта сумм слагаемых, обратно пропорциональных величине заданного признака, т.е. когда суммированию подлежат не сами варианты, а обратные им величины.

Средняя геометрическая определяется по формуле

Наиболее широкое применение средняя геометрическая получила для определения среднегодовых темпов роста в рядах динамики.

При выборе вида средней следует исходить из реального экономического смысла.

Разновидностью средней являются мода и медиана. Эти величины также используются в качестве характеристик вариационного ряда.

Мода (М₀) - варианта, встречающаяся в изучаемой совокупности чаще всего, т.е. варианта, которой соответствует наибольшая частота.

Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой располагается наибольшая частота, и будет модой.

В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Поэтому в модальном интервале необходимо определить модальную варианту. При этом надо иметь в виду, что при расчетах будет получено не точное, а некоторое условное значение моды, так как неизвестен характер распределения частоты внутри модального интервала.

Вычисление моды в интервальном ряду производится по следующей формуле:

,

где х_Мо - начало (нижняя граница) модального интервала (15);

i - величина интервала (2);

f_Мо - частота модального интервала (30);

f _Мо-1 - частота интервала, предшествующего модальному (20);

f _М0+1 - частота интервала, следующего за модальным (25).

Воспользуемся данными табл. 1.1. и рассчитаем моду:

Медиана (М_е)- варианта, находящаяся в средине ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Срединная варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле

,

где х_Ме - начало (нижняя граница) медианного интервала (15);

i- величина интервала (2);

- сумма накопленных частот ряда (100);

s_Ме-1 - накопленная частота вариант, предшествующих медианному (35);

f_Ме - частота медианного интервала (30).

Воспользуемся данными табл. 1.1. и рассчитаем медиану. В табл. 1.1. Ме лежит между 50 и 51 частотами, а они находятся в сумме накопленных частот, равной 65, поэтому интервал 15-17 является медианным. Определяем медиану

Для характеристики размеров колеблемости признаков в статистике применяется следующие показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации и др.

Размах вариации представляет собой разность между наибольшим (х_max) и наименьшим (x_min) значениями вариант, т.е.

R = х_max-х_min

Например, размах вариации производительности труда рабочих в бригаде (см.табл.1.1) равен: 21-9 = 12 шт. в смену. Среднее линейное отклонение определяется из отношения суммы, взятой по абсолютной величине (без учёта знака) отклонения всех вариант от средней арифметической, к объёму всей совокупности. Оно бывает незавершённое и взвешенное и определяется соответственно по формулам:

,

.

Дисперсия - это средняя из квадратов отклонений значений признака от его средней арифметической величины. Она определяется по формуле средней арифметической простой:

или средней арифметической взвешенной

Если имеются два взаимоисключающих друг друга варианта, то вариация признака называется альтернативной. Обозначая наличие признака - 1, а отсутствие - 0, и долю вариантов обладающих данным признаком - p, а долю вариантов, не обладающих им - q и замечая, что p+q=1, получаем среднюю:

Дисперсию альтернативного признака определяем по формуле:

Следовательно, дисперсия альтернативного признака

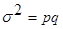
Среднее квадратичное отклонение - это корень квадратный из дисперсии - определяется по формулам средней арифметической простой:

или средней арифметической взвешенной

Среднее квадратическое отклонение альтернативного признака:

Мерой сравнения степеней колеблемости для двух, трех и более вариационных рядов служит показатель, который носит название коэффициента вариации и определятся по формуле:

Результаты расчета средней и показателей вариации студент должен представить в таблице по форме табл. 1.1.

 

Таблица 1.1.

 

Пример определения средней и показателей вариации.

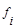
Прцент зольности угля	Число проб	Накопленные частоты	Центральная варианта хi
9-11 11-13 13-15 15-17 17-19 19-21					-5,8 -3,8 -1,8 +0,2 +2,2 +4,2	5,8 3,8 1,8 0,2 2,2 4,2	29,0 38,0 36,0 6,0 55,0 42,0	33,64 14,44 3,24 0,04 4,84 17,64	168,20 144,40 64,8 1,2 121,0 176,4
–		–		–	–		–
	–	–