 |
|
Найти общее решение уравнения.
Задача № 6.
Решить уравнение.
1.  2.
2. 
3.  4.
4. 
5. 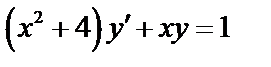 6.
6. 
7.  8.
8. 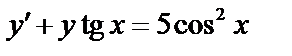
9.  10.
10. 
11. 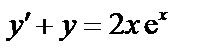 12.
12. 
13.  14.
14. 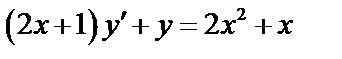
15. 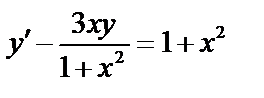 16.
16. 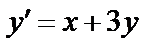
17.  18.
18. 
19.  .20.
.20. 
21. 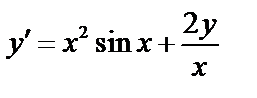 22.
22. 
23.  24.
24. 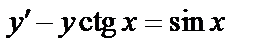
25.  26.
26. 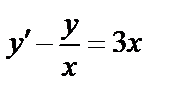
27.  28.
28. 
29.  30.
30. 
Задача № 7.
Найти общее решение уравнения.
1.  2.
2. 
3.  4.
4. 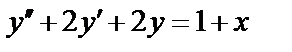
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 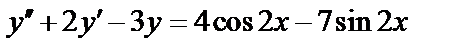
13. 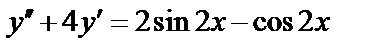 14.
14. 
15.  16.
16. 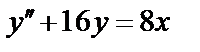
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 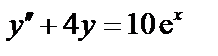
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
. Пример решения варианта контрольной работы.
1. Найти  ,
,  .
.
Решение:
Воспользуемся формулой (44):  .
.
Преобразуем уравнение к виду  ,
, 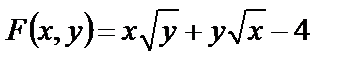 .
.
Находим 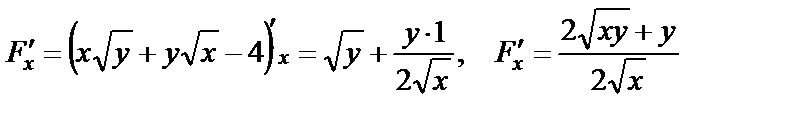

Следовательно,  ,
,
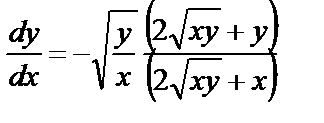 .
.
Ответ: 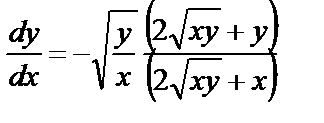
Задача № 2. Найти наибольшее и наименьшее значения функции в замкнутой области  .
.
| y |
| x |
| B |
| А |
| 1 |
| 1 |
| -1 |
| 0 |
| (D) |
 ,
, 
Решение:
I. Ищем критические точки функции 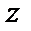 , лежащие внутри
, лежащие внутри  :
:

Решая систему уравнений  , находим критические точки
, находим критические точки  и
и  . Ни одна из них не лежит внутри области
. Ни одна из них не лежит внутри области  . Других критических точек функция не имеет.
. Других критических точек функция не имеет.
II. Находим наибольшее и наименьшее значения 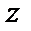 на границе заданной области.
на границе заданной области.
а) На участке АОВ имеем  , где
, где  .
.
Ищем наибольшее и наименьшее значения функции  на отрезке
на отрезке  :
:
1)  ;
;  при
при  ;
; 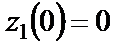 .
.
2) Находим  .
.
3) Сравнивая значения во внутренней критической точке  и на концах
и на концах  , заключаем: наибольшее значение
, заключаем: наибольшее значение 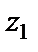 на отрезке
на отрезке 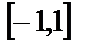 равно 5, т.е.
равно 5, т.е.  , а наименьшее значение
, а наименьшее значение 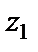 на этом отрезке равно нулю (в точке
на этом отрезке равно нулю (в точке  ).
).
б) На участке АВ имеем  где
где  :
:
Ищем наибольшее и наименьшее значения  на отрезке
на отрезке 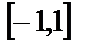 :
:
1)  внутри данного отрезка
внутри данного отрезка  при
при 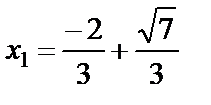 ;
;  .
.
2) Находим  .
.
3) Наибольшее значение  на отрезке
на отрезке  равно 5 в точках
равно 5 в точках 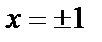 , а наименьшее значение
, а наименьшее значение  на этом отрезке равно 0,77 (в точке
на этом отрезке равно 0,77 (в точке 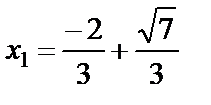 ).
).
Сопоставляя значения  на участках АОВ и АВ, приходим к выводу: на всей границе наибольшее значение функции
на участках АОВ и АВ, приходим к выводу: на всей границе наибольшее значение функции 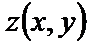 равно 5 (в точках А и В, а ее наименьшее значение равно 0 (в точке О).
равно 5 (в точках А и В, а ее наименьшее значение равно 0 (в точке О).
III.Внутри заданной замкнутой области  функция
функция  не имеет точек экстремума, ее наибольшее и наименьшее значения достигаются в точках, лежащих на границе этой области. В граничных точках
не имеет точек экстремума, ее наибольшее и наименьшее значения достигаются в точках, лежащих на границе этой области. В граничных точках  и
и  функция
функция  имеет наибольшее значение,
имеет наибольшее значение,  , а в граничной точке
, а в граничной точке  она имеет наименьшее значение,
она имеет наименьшее значение,  .
.
Задача № 3. Найти неопределенные интегралы, ответ проверить дифференцированием.
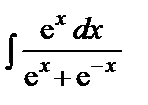 ,
,  ,
,  .
.
Решение:
 .
.
Проверка:  (верно).
(верно).

 .
.
Проверка: 
 (верно).
(верно).

 .
.
Проверка: 
 (верно).
(верно).
Задача № 4. Вычислить длину дуги кривой 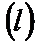 (Спираль Архимеда).
(Спираль Архимеда).

Решение: Воспользуемся формулой (55):
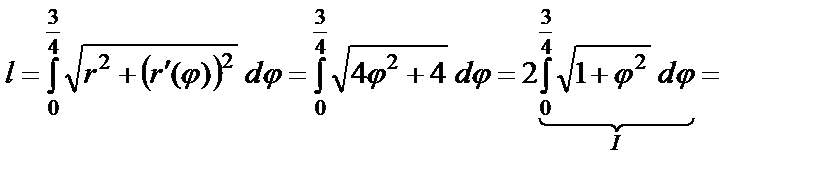
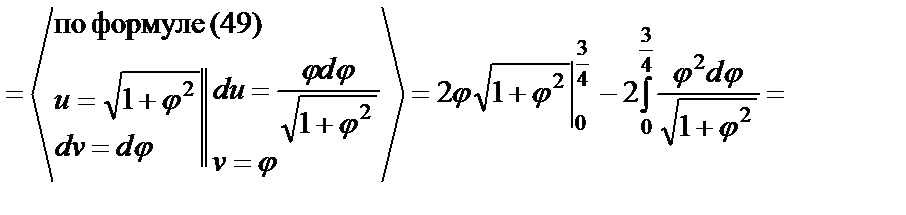

 .
.
Т.е. получили  .
.
Далее, перенося искомый интеграл  из правой части равенства в левую и заменяя интеграл, оставшийся в правой части равенства, по формуле 10 из таблицы интегралов, получим
из правой части равенства в левую и заменяя интеграл, оставшийся в правой части равенства, по формуле 10 из таблицы интегралов, получим

Таким образом, 
Имеем 
Ответ: 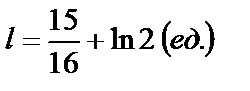 .
.
Задача 5 . Решить уравнение  .
.
Решение: Пусть  , тогда
, тогда  .
.
Подставив в уравнение, получим 
или
 (70)
(70)
1. Пусть 

2. Возвращаясь к (70), получаем:
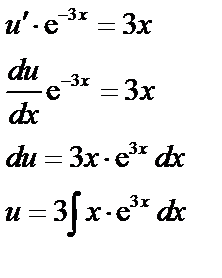
Вычислим 

Имеем 

3. Поскольку 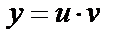 , то получаем общее решение
, то получаем общее решение 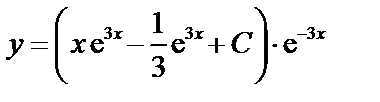 или
или  .
.
Ответ:  .
.
Задача 6.Найти общее решение уравнения  .
.
Решение: 1. Корнями характеристического уравнения  будут
будут 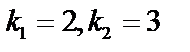 , следовательно,
, следовательно,  – общее решение соответствующего однородного уравнения.
– общее решение соответствующего однородного уравнения.
2. Так как в правой части уравнения  или
или  ,
, 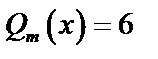 ,
,  ,
,  , то
, то
 ,
,
 .
.
Найдем  и
и  . Для этого вычислим
. Для этого вычислим
 ;
;
 .
.
Подставив значения  в исходное уравнение, получим тождество
в исходное уравнение, получим тождество


или  .
.
Приравнивая коэффициенты при  и
и  , имеем
, имеем

Решая систему, получим 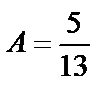 ,
, 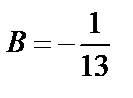 .
.
Частное решение неоднородного уравнения  .
.
3. Общее решение  ,
,
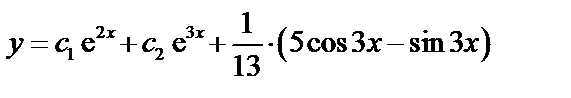 .
.
Ответ: 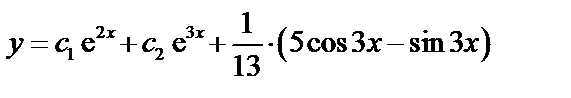 .
.