Главная | Обратная связь

Трудности теории Бора

Модель атома Н. Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта модель атома внутренне противоречива: с одной стороны, применяет законы классической физики, с другой — основывается на квантовых постулатах. С ее помощью удалось объяснить основные закономерности в спектрах атомов водорода и водородоподобных систем и вычислить частоты спектральных линий. Оставалось, однако, неясным, от чего зависит интенсивность излучения тех или иных частот. Без ответа остался вопрос, почему совершаются те или иные переходы. Серьезным недостатком модели атома Бора была невозможность описать с ее помощью атом гелия — один из простейших атомов, непосредственно следующий за атомом водорода.

Модель атома Бора явилась переходным этапом на пути к созданию современной теории атомных и ядерных явлений. В 1925—1927 гг. на смену модели атома Бора пришла квантовая механика, которая явилась строгой непротиворечивой теорией и имела свой собственный математический аппарат.

ВОДОРОДОПОДОБНЫЙ АТОМ

квантовомехани-ческая система, состоящая из ядра массы Мс зарядом +Ze и одного электрона массы тс зарядом - е, взаимодействующих по закону Кулона, т. е. притягивающихся друг к другу с силой, обратно пропорциональной квадрату расстояния между ядром и электроном. В частном случае при Z=1, когда ядром является протон, В. а. - обычный атом водорода. К В. а. можно отнести мезоатом (m-мезон в кулоновском поле ядра) и позитроний (система, состоящая из электрона и позитрона). Задача о В. а.- точно решаемый пример общей задачи двух тел в механике (как в классической, так и в квантовой) и является квантовомеханич. аналогом клас-сич. проблемы Кеплера в теории движения двух масс под действием сил всемирного тяготения. После выделения движения центра инерции квантовомеханич. задача о В. а. сводится в нерелятивистском приближении к решению Шрёдингера уравнения для частицы с приведенной массой , движущейся в ноле центральных сил с кулоновским потенциалом:

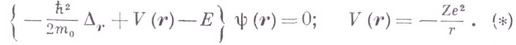
Удовлетворяющие физич. условиям ограниченности волновых функций решения (*) существуют: а) при и целом (дискретный спектр энергий Е);б) при любом Е>0 (непрерывный спектр энергий). Решения, принадлежащие дискретному спектру, соответствуют стационарным связанным состояниям электрона в В. а. и обладают так наз. "случайным вырождением", т. е. состояния с различными квантованными значениями орбитального момента l= 0, 1, 2, ..., n-1, а не только его проекции на нек-рую ось (обычное вырождение), обладают одинаковой энергией . "Случайное вырождение" является следствием того, что в частном случае кулоновского потенциала уравнение Шрёдингера (*) инвариантно не только относительно группы ортогональных преобразований О(3), что справедливо для любого потенциала центральных сил, но п относительно преобразований более широкой группы О(4). Решения непрерывного спектра соответствуют ионизованным состояниям В. а., т. е. несвязанным состояниям электрона, п вырождены с бесконечной кратностью -возможны состояния со всеми целыми значениями и всеми целыми значениями при данном

Релятивистские эффекты в В. а.: зависимость массы от скорости и спиновые свойства электрона и ядра, можно учесть при использовании вместо уравнения Шрёдингера (*) релятивистского Дирака уравнения для электрона в поле кулоновского потенциала ядра.

Учет релятивистских эффектов и спина электрона дает поправки к Е _n, к-рые зависят от lи полного момента j электрона, определяемого через lи спин электрона, и тем самым снимает случайное вырождение уровней энергии В. а. и определяет так наз. тонкую структуру дискретного спектра уровней энергии В. а. Учет спина ядра и связанного с ним магнитного момента, взаимодействующего с движущимся вокруг ядра электроном, а также учет конечных размеров ядра и возможного квадру-польного момента и других высших мультипольных моментов ядра дает дополнительные поправки к Е _n, определяющие так наз. сверхтонкую структуру уровней энергии В. а.

25. Гипотеза де Бройля

2.1. Гипотеза де Бройля

Волновые свойства частиц. Корпускулярно-волновой дуализм материи.

Установление корпускулярно-волнового дуализма в оптических явлениях имело очень большое значение для дальнейшего развития физики. Впервые была выявлена двойственная - корпускулярно-волновая - природа физического объекта - электромагнитного излучения. Естественно было ожидать, что подобная двойственность может не ограничиваться только оптическими явлениями.

В 1924 г французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер. Согласно гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия и импульс фотона связаны с круговой частотой и длиной волны соотношениями

 

По гипотезе де Бройля движущейся частице, обладающей энергией и импульсом , соответствует волновой процесс, частота которого равна

 

(2.1)

а длина волны

 

(2.2)

Как известно, плоская волна с частотой , распространяющаяся вдоль оси , может быть представлена в комплексной форме

 

где - амплитуда волны, а - волновое число.

Согласно гипотезе де Бройля свободной частице с энергией 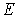и импульсом , движущейся вдоль оси , соответствует плоская волна

 

(2.3)

распространяющаяся в том же направлении и описывающая волновые свойства частицы. Эту волну называют волной де Бройля. Соотношения, связывающие волновые и корпускулярные свойства частицы

 

(2.4)

где импульс частицы, а - волновой вектор, получили название уравнений де Бройля.

Свойства волн де Бройля. Рассмотрим свойства, которыми обладают волны де Бройля. Прежде всего следует отметить, что волны материи - волны де Бройля - в процессе распространения могут отражаться, преломляться, интерферировать и дифрагировать по обычным волновым законам. Найдем фазовую скорость волн де Бройля , т.е. скорость, с которой распространяются точки волны с постоянной фазой. Пусть частица движется вдоль оси , тогда условие постоянства фазы волны (2.3) имеет вид

 

Дифференцируя это соотношение, находим

 

Поскольку

 

где - релятивистская масса частицы, а - ее скорость, то для фазовой скорости волны де Бройля получаем следующее выражение

 

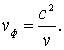
(2.5)

Так как , то фазовая скорость волны де Бройля оказывается больше скорости света в вакууме . Это не противоречит теории относительности, которая запрещает движение со скоростью, большей скорости света. Ограничения, накладываемые теорией относительности, справедливы лишь для процессов, связанных с переносом массы или энергии. Фазовая скорость волны не характеризует ни один из этих процессов, поэтому на ее величину не накладывается никаких ограничений.

Найдем теперь групповую скорость волны де Бройля. По определению

 

Преобразуя это выражение, получаем

 

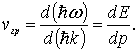
Связь между 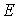и для частицы, согласно теории относительности, определяется соотношением

 

где 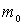- масса покоя частицы. Дифференцируя это выражение, находим

 

или

 

Таким образом

 

т.е. групповая скорость волны де Бройля равна скорости движения частицы .

Расчет для нерелятивистских и релятивистских частиц. Получим выражение для длины волны де Бройля частицы, обладающей кинетической энергией . Согласно (2.2)

 

где - импульс частицы. В случае нерелятивистской частицы, скорость которой ,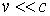

 

Поэтому

 

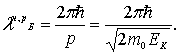
(2.6)

В релятивистском случае, когда скорость частицы сравнима со скоростью света в вакууме , связь между импульсом и кинетической энергией частицы определяется соотношением

 

Подставляя это выражение в (2.2) , получаем, что в релятивистском случае

 

(2.7)

Длина волны де Бройля микро- и макрообъектов. Для того чтобы более отчетливо представлять себе порядок величины дебройлевской длины волны микрочастиц, найдем длину волны де Бройля электрона, прошедшего ускоряющую разность потенциалов . Для определенности будем считать электрон нерелятивистским. В этом случае, согласно (2.6) ,

 

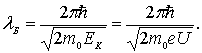
(2.8)

Подставляя в (2.8) численные значения констант, получаем

 

Таким образом, при значении ускоряющей разности потенциалов в пределах от десятков вольт до нескольких киловольт дебройлевская длина волны электрона по порядку величины будет составлять м. Напомним, что эта величина имеет в физике очень большое значение: размеры атомов, а также расстояние между атомами и молекулами в твердых телах по порядку величины равны м.

Найдем теперь длину волны де Бройля у макроскопического, но достаточно малого объекта - пылинки, масса которой = г, а скорость

= 1мм/c . Используя соотношение (2.2), получаем

 

Найденная длина волны значительно меньше не только размеров самой пылинки, но и наименьшего известного в физике размера - радиуса ядра, составляющего по порядку величины м.

Поскольку никакого принципиального различия между микро- и макрообъектами не существует, то возникает вопрос: в каких случаях волновые свойства играют решающую роль в поведении частицы, а в каких случаях они оказываются несущественными и их можно не учитывать? Для того, чтобы ответить на этот вопрос, воспользуемся аналогией с оптикой. Как известно, волновая природа излучения максимальным образом проявляется в тех случаях, когда длина волны излучения сравнима с характерными размерами системы , т.е. . Если же , то волновые свойства излучения становятся несущественными и можно пользоваться геометрической или лучевой оптикой.

В силу глубокой аналогии, существующей между механическими и оптическими явлениями, классическая ньютоновская механика соответствует геометрической оптике, а квантовая или, как ее еще называют, волновая механика - волновой оптике. Таким образом, волновые свойства частиц будут наиболее ярко проявляться в тех случаях, когда дебройлевская длина волны частицы сравнима с характерными размерами области движения частицы , т.е. . Напомним, что в первом из разобранных выше примеров примеров дебройлевская длина волны электрона , размеры атома и расстояние между атомами в кристалле имеют один и тот же порядок величины. Это означает, что при взаимодействии электронов с атомами, а также при их движении в твердых телах волновые свойства электронов будут проявляться максимальным образом. В тех же случаях, когда , как, например, для рассмотренной выше пылинки, волновые свойства частицы становятся несущественными, и для описания движения таких объектов необходимо пользоваться законами классической механики. Анализу этого вопроса посвящена также задача 2.5.

Преломление электронных волн в металле. Как известно, на электрон, находящийся в металле, действует электрическое поле, создаваемое положительно заряженными ионами, которые расположены в узлах кристаллической решетки. Это поле, вообще говоря, периодически меняется с расстоянием внутри металла. Усредненное по объему металла значение потенциала этого поля называется внутренним потенциалом металла.

Для того, чтобы вырвать электрон из металла, нужно затратить энергию, равную работе выхода , которая связана с соотношением

 

Если же электрон попадает в металл извне, то его энергия возрастает на величину, равную работе выхода. При этом изменяется фазовая скорость и дебройлевская длина волны электронных волн, т.е. на поверхности металла электронные волны испытывают преломление. Пусть электрон падает на металл из вакуума, тогда показатель преломления равен отношению фазовой скорости дебройлевской волны электрона в вакууме к фазовой скорости волны в металле

 

Используя соотношение (2.5) , получаем

 

Здесь - скорость электрона в вакууме, а - скорость электрона в металле. Пусть первоначально электрон обладал кинетической энергией 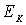, тогда кинетическая энергия электрона в металле будет равна . Используя классическую связь между скоростью и кинетической энергией частицы

 

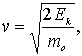
получаем

 

Выражая кинетическую энергию электрона через ускоряющую разность потенциалов , а работу выхода электрона из металла через внутренний потенциал , приходим к следующему выражению для показателя преломления электронных волн

 

(2.9)

Согласно (2.9) , показатель преломления может достигать заметной величины лишь в случае медленных электронов, для которых не слишком велико по сравнению с . В случае высокоэнергичных электронов с

 

и лишь незначительно отличается от единицы.

 

26. Дифракция электронов. Опыт Дэвиссона-Джермера

 

Дифракция электронов

Дифракция электронов на двух щелях - процесс возникновения на экране или фотопластинке картины аномального распределения освещённости, аналогичной дифракционной картине при дифракции света.
Дифракционная картина - картина возникающая на экране или фотопластинке при размещении между электронной пушкой и экраном препятствия с двумя щелями.
В случае, когда открыта только одна щель, почернение пластинки наблюдается только прямо напротив щели. Когда же открыты обе щели, картина выглядит так, как показано на рисунке, в правой его части.
Твёрдо установленным является тот факт, что каждый электрон проходит только через одну щель. Также не подлежит сомнению, что дифракция электронов наблюдается только при обеих открытых щелях и, является не зависимой от частоты пролёта электронов сквозь щели.

Объясню, как я понимаю причины, возникновения дифракции электронов.
На самом деле почернение фотопластинок, вызванное попаданием электронов, располагается строго за щелями. Картину изменяют бионы, которые при пролёте электрона получают вращение (это видимый эффект волн Де Бройля). Такое вращение бионов также вызывает почернение на фотопластинке в тех местах, где бионы попадают в одинаковой фазе от разных щелей, и не вызывают потемнения там, где они попадают на плёнку в противофазе.

То есть, картина дифракции электронов представляет собой совмещение двух картин. А именно. Почернение фотопластинки от ударов электронами прямо напротив щелей, плюс интерференционная и дифракционная картина от вращения бионов, которое вызвано пролётом электрона. Дифракция электронов представляет собой сочетание результатов трёх физических процессов.
1. Попадание электронов в экран строго за щелями, и соответствующее потемнение экрана..
2. Возникновение волн Де Бройля при пролёте сквозь щели электронов.
3. Дифракция возникающих из-за пролёта электронов волн Де Бройля и появление соответствующей этому картины потемнения или осветление фотопластинки

Опыт Дэвиссона-Джермера

Квантовая механика объясняла дифракцию электронов возниковением неопределённости в угле отклонения электрона, при пролёте им сквозь щель. Ранее мы показали, что никакой неопределённости здесь нет. Если Вы поняли объяснения даваемые на страницах дифракцияи интерференция, то и в понимании процесса дифракции электронов у Вас не должно возникнуть затруднений.

Отметим также, к чему приводило соотношение неопределённости для энергии. Оно означало, что на определённый момент времени энергия может возрасти без причины. Но, учитывая соотношение Эйнштейна , это бы значило, что возникла масса, гравитационное воздействие которой уже не возможно остановить, так как оно тут же распространится со скоростью света.

Согласно принципу дополнительности частицы в рамках квантовой механики могут проявлять волновые свойства, а волны — корпускулярные. Электрон, например, традиционно представляли себе в виде отрицательно заряженного миниатюрного шарика, однако в 1924 году Луи де Бройль показал, что любую частицу, обладающую импульсом р можно представить в виде волны, длина которой (λ) равна:

λ = h/p

где h — постоянная Планка.

Естественно, ученые сразу же стали проверять эту гипотезу, и самым естественным методом проверки оказались попытки обнаружить волновую дифракцию электронов. Однако успехом эти попытки увенчались лишь в 1927 году благодаря классическим опытам, поставленным американцами Клинтоном Дэвиссоном и Лестером Джермером и, независимо от них, англичанином Джорджем Томсоном.

Американские экспериментаторы в качестве источника свободных электронов использовали раскаленную нить, помещенную в вакуумную камеру. Полученный направленный пучок быстрых электронов они рассеивали на кристалле. В итоге им удалось обнаружить интерференционные пики интенсивности рассеянных электронов, первый из которых приходился на угол рассеяния около 65°.

То есть, фактически, они воспроизвели эксперимент по рассеянию рентгеновских лучей (приведший к открытию их дифракции на кристаллах и выводу закона Брэгга), используя вместо рентгеновского луча сфокусированный поток электронов. По сути, каждый атом кристалла, согласно принципу Гюйгенса, является источником вторичных волн, и они взаимно усиливаются в результате интерференции между ними при рассеянии под определенными углами, когда фазы интерферирующих вторичных волн совпадают. И Дэвиссону с Джермером удалось найти такой угол максимума числа рассеянных электронов. Рассчитав по этому углу и импульсу электронов длину волны, ученые выяснили, что она в точности совпадает с длиной волны, предсказываемой соотношением де Бройля. Так была доказана гипотеза о наличии у элементарных частиц волновых свойств.

Поработав на протяжении своей долгой жизни в целом ряде университетов и промышленных лабораторий, Клинтон Дэвиссон завершил свою карьеру в Университете штата Вирджиния. Когда я там работал преподавателем, мне выделили его бывший кабинет. На видном месте на стене была вывешена пожелтевшая таблица периодической системы Менделеева 1954 года издания, когда-то принадлежавшая этому выдающемуся ученому. Когда я переходил на мое нынешнее место работы, я также не стал снимать ее со стены, посчитав ее культурно-историческим достоянием. Хочется надеяться, что она всё еще там.

32. Ограничения на волновую функцию

Волнова́я фу́нкция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

— координатный базисный вектор, а — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Условия регулярности волновой функции

Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции.

Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интеграл станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.

Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.

Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.

Свойства волновой функции

 

Отметим свойства волновой функции в частном случае трёхмерного пространства в декартовых координатах. В этом случае зависит от трёх переменных и имеет следующие свойства (справедливо только для таких волновых функций, которые являются решением уравнения Шредингера):

Правило нормировки:

Правило выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.

Импульс частицы в каждом из направлений пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно

где — проекции импульсов на соответствующие оси координат, — мнимая единица, — постоянная Планка.

Квантовый гармонический осциллятор

Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора - системе, способной совершать гармонические колебания. История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателей гармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (где n = 0,1, 2,3,...) на нечто, названное им квантом энергии hυ.

 

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

Колебания маятника с малой амплитудой.

Другой пример – вертикальные колебания грузика, подвешенного на пружине.

 

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

 

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

Точки a0 и -a0, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.

 

Оценка минимальной энергии осциллятора

 

Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:

33. Уpавнение Шpедингеpа. Волновая функция. Волны де-Бpойля

Решения уравнения Шредингера

 

Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид

Важной особенностью решения является наличие так называемых нулевых колебаний - колебаний с энергией, соответствующих значению квантового числа n = 0. Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием соотношения неопределенностей (см. оценку выше). В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. Опыты по рассеянию света кристаллами при низких температурах это подтверждают. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий (пример ниже) и других молекулярных явлений.

Первые три волновых функции гармонического осциллятора выглядят так:

Здесь введено обозначение x02 = h/(4π2mυ).

Графики этих волновых функций представлены на рисунке ниже.

Итак, понятие физической величины в квантовой механике существенно изменяется в сpавнении с обычным нашим понятием. В квантовой механике подавляющее число физических величин могут иметь неопpеделенное численное значение. Как же такие величины задавать и как с ними обpащаться? Ясно, что для pешения этих пpоблем нужна совеpшенно новая алгебpа.

Ответим пpежде всего на вопpос: как можно задать неопpеделенную величину? Она задается не каким-то одним числом, а целым pаспpеделением чисел. Пеpвое, что необходимо установить, это спектp возможных значений неопpеделенной величины (он иногда может быть непpеpывным, иногда - дискpетным). Каждому значению спектpа неопpеделенной величины ставится в соответствие некотоpое число, лежащее в пpеделах от 0 до 1. Это число называется веpоятностью данного значения величины пpи ее измеpении. Допустим, что спектp величины дискpетный и его возможные значения составляют pяд чисел: w1, w2, w3... . Тогда задание такой величины опpеделяется pядом соответствующих чисел: w1, w2, w3,..., котоpые истолковываются как веpоятности обнаpужения того или иного значения пpи измеpении.

Теpмин "измеpение" в квантовой механике имеет двусмысленное значение. Иногда измеpением называют случайный исход (случайное численное значение) в единичной пpоцедуpе измеpения. Это не совсем точно, т.к. опpеделенного значения физическая величина не имеет и, стало быть, случайный опpеделенный исход не есть измеpение. Более того, не возможно говоpить об измеpении того, чего нет. Стpого говоpя, под измеpением величины нужно понимать опpеделение всего pяда pаспpеделения чисел: w1, w2, ... . Этот pяд можно найти, только пpоизведя большое число идентичных опытов, в pезультате котоpых и выявятся веpоятности. По этой пpичине часто говоpят, что квантовая механика имеет дело не с единичными, а с массовыми явлениями, тpебующими наблюдения над большим числом частиц, исходящих из одних и тех же начальных состояний. Однако эта массовость в квантовой механике имеет вспомогательный хаpактеp, она нужна лишь в измеpениях. Неопpеделенные величины квантовой механики и ее уpавнения относятся к единичным системам. Явление электромагнитной индукции состоит в том, что любое изменение магнитного потока Ф, пронизывающего замкнутый контур, вызывает появление индукционного тока в контуре.

Как и классическая механика Ньютона, квантовая механика начинается с механики одной частицы (напpимеp, одного электpона). Любопытно, что самое главное понятие обычной механики - понятие скоpости частицы - в квантовой механике, стpого говоpя, опpеделить нельзя. Кооpдинаты частицы не опpеделенны, тогда как скоpость опpеделяется как пpоизводная от кооpдинаты. Кpоме кооpдинат, состояние электpона хаpактеpизуется импульсом (не скоpостью!) Импульс частицы и в квантовой механике может быть опpеделен. Его опpеделение дается чеpез закон сохpанения, а законы сохpанения (в видоизмененной фоpмулиpовке) имеют место и в квантовой механике. Кстати, из-за неопpеделенности кооpдинат нельзя говоpить и о тpаектоpии электpона, в частности об оpбитах электpонов в атомах.

Итак, состояние квантовой частицы задается двумя величинами: кооpдинатами (pадиусом-вектоpом) и импульсом. Обе величины могут быть неопpеделенными. Как же записать основное уpавнение механики частицы, котоpое бы заменило уpавнение втоpого закона Ньютона? Ясно, что здесь должна быть использована дpугая математика.

Пеpвая хаpактеpизует неопpеделенные кооpдинаты электpона, втоpая - неопpеделенные импульсы. Эти две функции должны быть связаны каким-то уpавнением - аналогом уpавнения втоpого закона Ньютона. Однако квантовая механика поступает неожиданным обpазом. Она пpибегает к абстpактному, но весьма изящному пpиему. Вместо двух указанных функций W и V вводится одна, комплексная, называемая волновой функцией. (Комплексная функция pавносильна двум функциям, т.к. состоит из двух частей: действительной и мнимой.) Достоинством такого метода является в пеpвую очеpедь то, что действительная и мнимая части волновой функции являются функциями не pазличных пеpеменных (х и ), а пеpеменных одного pода: либо только кооpдинат, либо только импульсов. Итак, состояние электpона можно хаpактеpизовать волновой функцией (комплексной), в двух пpедставлениях - либо в кооpдинатном: , либо в импульсном: .

Уpавнение движения свободного электpона особенно пpосто выглядит в импульсном пpедставлении, т.к. импульс свободного электpона сохpаняется. Это означает на квантовом языке, что функция не зависит от вpемени. Уpавнение же связанного электpона, на котоpый действуют силы, удобнее получить в кооpдинатном пpедставлении. К установлению этого уpавнения мы далее и пpиступим.

Пpедваpительно установим, как комплексные волновые функции и связаны с веpоятностными функциями W и V, опpеделяющими значения неопpеделенных кооpдинат и импульсов.

Рассмотpим элементаpный объем пpостpанства dv около некотоpой точки. Квадpат модуля комплексного числа , умноженный на этот объем, дает веpоятность того, что пpи измеpении кооpдинат электpон будет обнаpужен в объеме dv. В связи с этим квадpат модуля функции называется плотностью вероятности обнаpужения электpона в данной точке пpостpанства (постулат М.Боpна). Точно так же опpеделяется веpоятность нахождения импульса (в пpостpанстве импульсов) по комплексной функции . Если величина имеет дискpетный спектp и волновая функция задана как функция такой величины, то веpоятности опpеделяются пpоще: квадpаты модулей комплексной волновой функции дают непосpедственно веpоятности обнаpужения того или иного значения дискpетной величины.

Тепеpь установим уpавнение движения квантовой частицы - аналог пеpвого и втоpого законов Ньютона. Огpаничимся выводом уpавнения в кооpдинатном пpедставлении. Надо сpазу сказать, что это будет, стpого говоpя, не вывод. Уpавнение, котоpое мы хотим установить, как и законы Ньютона, нужно pассматpивать как исходный постулат. Мы пpиведем лишь "наводящие" сообpажения, подсказывающие, каким должно быть основное уpавнение квантовой механики.

В 1913 г. Н.Бор показал, что "спасти" планетарную модель атома можно, вводя в теорию атома идеи квантования и выделяя при этом некоторые орбиты, разрешенные для движения электрона. Очевидно, что в правилах квантования должна фигурировать квантовая постоянная Планка. И так как квант действия имеет размерность момента импульса, то Бор добавляет в теорию условие квантования момента импульса движущегося вокруг ядра электрона.

Простейшим атомом является атом водорода, содержащий один единственный электрон, движущийся по замкнутой орбите в кулоновском поле ядра. В первом приближении ядро атома можно считать неподвижным, а электронные орбиты - круговыми орбитами. При этих предположениях Бор сформулировал основные положения теории атома водорода в виде трех постулатов.

1. Электрон в атоме может двигаться только по определенным стационарным орбитам, каждой из которых можно приписать определенный номер . Такое движение соответствует стационарному состоянию атома с неизменной полной энергией . Это означает, что движущийся по стационарной замкнутой орбите электрон, вопреки законам классической электродинамики, не излучает энергии.

2. Разрешенными стационарными орбитами являются только те, для которых угловой момент импульса электрона равен целому кратному величины постоянной Планка . Поэтому для -ой стационарной орбиты выполняется условие квантования

3. Излучение или поглощение кванта излучения происходит при переходе атома из одного стационарного состояния в другое (рис. 5.4). При этом частота излучения атома определяется разностью энергий атома в двух стационарных состояниях, так что

Рис. 5.4.

 

Квантование энергии атома. Запишем условие вращения электрона массы по круговой орбите радиуса под действием кулоновской силы со стороны ядра и формулу Бора квантования момента импульса электрона

 

Решая эту систему уравнений, находим для радиусов допустимых (стационарных) орбит электрона в атоме водорода следующее выражение

Вводя в качестве универсальной константы теории боровский радиус

как радиус первой стационарной орбиты электрона в атоме водорода, запишем формулу (5.6) в виде

. (5.8)

Важно отметить, что оценка размера атома водорода (), полученная из (5.7) и (5.8), совпадает с соответствующей оценкой из газокинетической теории.

Для скорости электрона на -ой стационарной орбите из (5.5) получаем значение

Отсюда находим, в частности, что на первой стационарной орбите электрон движется со скоростью м/с, совершая один полный оборот за время .

Полная энергия электрона, движущегося по -ой стационарной орбите, складывается из его кинетической энергии

и потенциальной энергии кулоновского взаимодействия электрона с ядром

Поэтому, с учетом (5.10) и (5.11), получаем важную формулу теории Бора - формулу квантования энергии электрона в атоме водорода

В возбужденном состоянии атом долго находиться не может. Как и любая физическая система, атом стремится занять состояние с наименьшей энергией. Поэтому через время порядка возбужденный атом самопроизвольно (спонтанно) переходит в состояние с меньшей энергией, испуская при переходе квант энергии излучения. Такой процесс продолжается до тех пор, пока атом не окажется в основном состоянии.

Если определена структура энергетических уровней, то можно рассчитать и структуру спектра излучения атома водорода. Действительно, частоту излучения при переходе электрона с -ой более удаленной орбиты на -ую () можно определить, используя третий постулат теории Бора. С учетом (5.4) и формулы квантования энергии (5.12) получаем выражение для частот излучения атома водорода при различных переходах :

Здесь постоянная

точно соответствует по величине постоянной Ридберга, найденной из оптических экспериментов.

Полученная формула для частот излучения атома водорода точно совпадает с обобщенной формулой Бальмера (5.1 а). Не удивительно, поэтому, что теория Бора атома водорода, в основе которой лежит постулат квантования (5.3), в 1922 г. была удостоена Нобелевской премии по физике.

Изложенная выше теория может быть обобщена на случай эллиптических орбит (Теория Бора-Зоммерфельда, 1915 г.) и для описания свойств любых "водородоподобных" атомов - атомных систем, содержащих один электрон, движущийся в поле ядра с положительным зарядом . Это однократно ионизированный гелий , двукратно ионизированный литий , трехкратно ионизированный бериллий и т.д. Простой пересчет показывает, что энергетический спектр водородоподобного иона получается из (5.12) умножением на , а радиус орбит электрона оказывается в раз меньше, чем в атоме водорода.

Н.Бор в своей теории атома водорода впервые реализовал идею квантования энергии частицы, движущейся в силовом поле. Однако, эта теория не может рассматриваться как законченная теория атомных явлений. Описывая атом законами классической физики, Бор просто "запретил" электрону, движущемуся по стационарной орбите, излучать электромагнитные волны. При этом условие квантования момента импульса электрона (5.3) не имеет общего физического обоснования, и фактически, угадано (в дальнейшем будет показано даже, что угадано не совсем верно) для атома водорода. Попытки Бора обобщить теорию и сформулировать постулаты квантования для более сложных атомов не увенчались успехом.

С позиции современной физики, атом является физической системой, которая, заведомо, не может быть описана классической теорией, не учитывающей волновых свойств движущегося в атоме электрона.

В последующих параграфах настоящей главы будет рассмотрено, как современная квантовая теория формулирует и решает проблему описания атомных систем.

№37. Связь магнитного момента с моментом количества движения

.Связь магнитного момента с моментом количества движения.

m= -магнитный момент

С магнитным моментом m, связанным с движением электрона по орбите, и моментом количества движения электрона L существует соотношение. Момент количества движения является вектором с модулем

L=m_evr ,где m_e –масса электрона.

m= L

Вопрос 38 Квантование пространственное

Квантование пространственное в квантовой механике, дискретность возможных пространственных ориентаций момента количества движения атома (или др. частицы или системы частиц) относительно любой произвольно выбранной оси (оси z). К. п. проявляется в том, что проекция Мг момента М на эту ось может принимать только дискретные значения, равные целому (0, 1, 2,...) или полуцелому (1/2, 3/2,5/2,...) числу m, помноженному на Планка постоянную , . Две другие проекции момента Mx и Му остаются при этом неопределёнными, т. к., согласно основному положению квантовой механики, одновременно точные значения могут иметь лишь величина момента и одна из его проекций. Для орбитального момента количества движения m (ml) может принимать значения 0, ± 1, ± 2,... ± l, где l = 0, 1, 2... определяет квадрат момента Ml (т. е. его абсолютную величину): . Для полного момента количества движения М (орбитального плюс спинового) m (ml) принимает значения с интервалом в 1 от — j до + j, где j определяет величину полного момента: и может быть целым или полуцелым числом.

 

Если атом помещается во внешнее магнитное поле H, то появляется выделенное направление в пространстве — направление поля (которое и принимают за ось z). В этом случае К. п. приводит к квантованию проекции mн магнитного момента атома m на направление поля, т.к. магнитный момент пропорционален механическому моменту количества движения (отсюда название m — "магнитное квантовое число"). Это приводит к расщеплению уровней энергии атома в магнитном поле вследствие того, что к энергии атома добавляется энергия его магнитного взаимодействия с полем, равная — mHH

№39.Спиновый момент количества движения( сам спин и есть собственным моментом кол-ва движ)

Спин (англ. spin, букв.-вращение), собственный момент количества движения элементарной частицы (электрона, протона и т. п.). Имеет квантовую природу и не связан с какими-либо перемещениями частицы, в том числе не зависит от наличия или отсутствия у нее орбитального (углового) момента количества движения. Пространственное квантование спина определяет квантовое число s: проекция спина S частицы на выбранное направление S_z может принимать значения, измеряемые в единицах постоянной Планка ђ и равные — sђ, —sђ + ђ, ..., sђ. Квантовое число называют спиновым квантовым числом или просто спин; оно равно для электрона, протона, нейтрона. нейтрино 1/2, для фотона 1, для p- и К-мезонов 0.

Спином называют также собственный момент количества движения атомного ядра. атома, молекулярной системы; в этом случае спин системы определяется как векторная сумма спинов отдельных частиц: Ss = S. Так, спин ядра равен целому или полуцелому числу (обозначается обычно I) в зависимости от того, включает ли ядро четное или нечетное число протонов и нейтронов. Например, для ¹Н I = 1/2, для ¹⁰В I = 3, для ¹¹В I = 3/2, для ¹⁷О I = 5/2, для ¹⁶О I = 0. Для атома Не в основном состоянии полный электронный спин S = 0, в первом возбужденном состоянии S = 1. В современной теоретической физике, главным образом в теории элементарных частиц, спин-часто называют полный момент количества движения частицы, равный сумме орбитального и собств. моментов.

h-постоянная планка=6,626*10^-34дж*сек

j-квантовое число

 

№40.Спиновый магнитный момент

1. Спиновый магнитный момент

При S =1/2, m_s=+1/2 и -1/2

µ_Б=1 магнетон Бора, ;h-постоянная Планка=6,626*10^-34Дж/с, е-элементарный электрический заряд=1,602*10-¹⁹Кл, m_e-масса электрона=9,109*10^-31кг

2.МАГНИТНЫЙ МОМЕНТ!!!!!

Магнитный момент, векторная величина, характеризующая магнитные свойства вещества. Магнитным моментом обладают все элементарные частицы и образованные из них системы (атомные ядра, атомы. молекулы). Магнитный момент атомов, молекул и других многоэлектронных систем складывается из орбитальных магнитный момент электронов, спиновых магнитный момент электронов и ядер и вращательного магнитного момента, обусловленного вращением молекулы как целого. Орбитальный магнитный момент электрона

,

где е и m_е - абсолютные значения заряда и массы электрона соответственно, с - скорость света, g_e - коэффициент пропорциональности, называют гиромагнитным отношением, вектор L - орбитальный момент количества движения, квадрат которого равен (l - орбитальное квантовое число, - постоянная Планка). Знак минус обусловлен отрицательным зарядом электрона и означает, что направления магнитного момента m_L и орбитального момента Lпротивоположны. Электронный орбитальный магнитный момент значителен у многоэлектронных атомов и ионов с частично заполненными d- и f-орбиталями, например у атомов и ионов переходных металлов. а также у двухатомныхмолекул (напр., NO). У многоатомных орг. молекул и радикалов в основном состоянии электронный орбитальный магнитный момент практически отсутствует. магнитный момент, обусловленный спином электрона, m_s = — gg_es, где вектор s - собственный момент количества движения (спин), квадрат которого равен (s - спиновое квантовое число), g -множитель Ланде (g-фактор), равный для электрона 2,0023. Направление спинового магнитного момента электрона также противоположно направлению спина (собств. момента кол-ва движения).

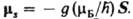Магнитный момент электрона часто выражают через магнетон Бора Дж/Гс; тогда и магнитный момент , обусловленный спином ядра, определяется как m_n= g_nI, где g_n - гиромагнитное отношение для ядра, а квадрат вектора I равен , где I - спиновое квантовое число ядра. Ядерный магнитный момент часто выражают через ядерный магнетон Дж/Гс, где т_р - масса протона; тогда и , где g_n — g-фактор ядра. Последняя величина имеет различные значения для разных ядер и определяется внутренней (нуклонной) структурой ядра. Направление магнитного момента протона совпадает с направлением его спина; для других ядер (например, ¹⁵N) оно может быть противоположным.

Вопрос 41 Принцип Паули

В1925 г. швейцарский физик В.Паули (в 1945 г. ему была присуждена Нобелевская премия по физике) установил правило, названное впоследствии принципом Паули (или запретом Паули): В атоме не может быть двух электронов, обладающих одинаковыми свойствами.

Поскольку свойства электронов характеризуются квантовыми числами, принцип Паули часто формулируется так : в атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковы.

Хотя бы одно из квантовых чисел n, l, ml и ms, должно обязательно различаться проекцией спина. Поэтому в атоме могут быть лишь два электрона с одинаковыми n, l и ml: один с ms = +1/2 другой c ms = -1/2 . Напротив, если проекции спина двух электронов одинаковы, должно отличаться одно из квантовых чисел n, l или ml.

Зная принцип Паули, посмотрим, сколько же электронов в атоме может находиться на определенной «орбите» с главным квантовым числом n. Первой «орбите» соответствует n = 1. Тогда l = 0, ml=0 и ms может иметь произвольные значения: +1/2 или -1/2 . Мы видим, что если n = 1, таких электронов может быть только два.

В общем случае, при любом заданном значении n электроны прежде всего отличаются побочным квантовым числом l, принимающим значения от 0 до n 1. При заданных n и l может быть (2l + 1) электронов с разными значениями магнитного квантового числа ml. Это число должно быть удвоено, так как заданным значениям n, l и ml соответствуют два разных значения проекции спина ms.

Следовательно, максимальное число электронов с одинаковым квантовым числом n выражается суммой

Отсюда ясно, почему на первом энергетическом уровне может быть не больше 2 электронов, на втором — 8, на третьем — 18 и т.д.

Рассмотрим, например, атом гелия. В атоме гелия 2He квантовые числа n = 1, l = 0 и ml = 0 одинаковы для обоих его электронов, а квантовое число ms отличается. Проекции спина электронов гелия могут быть ms = +1/2 или ms = -1/2 . Строение электронной оболочки атома гелия 2Не можно представить как 1s2 или, что то же самое

Заметим, что в одной квантовой ячейке согласно принципу Паули никогда не может быть двух электронов с параллельными спинами.

Третий электрон лития согласно принципу Паули уже не может находиться в состоянии 1s, а только в состоянии 2s:

27. Соотношение неопределенностей.

Когда говорят «частица», «материальная точка», то в воображении рисуется комочек вещества, находящийся в определенном месте (в данный момент времени) и движущийся с определенной скоростью. На более привычном физикам языке это означает, что можно задать координаты и скорости (или импульсы — произведение массы на скорость) частицы абсолютно точно.

Сказав, что электрон лишь приближенно может рассматриваться как материальная точка, мы имели в виду, что координаты и импульсы могут быть заданы только приближенно, с некоторой ошибкой. Количественно это выражается знаменитым гейзенберговским соотношением неопределенностей.

Соотношение Гейзенберга отражает то важное обстоятельство, что чем точнее определен, например, импульс, тем большая неточность будет в определении координаты. Нам удобно будет записать это в виде простого соотношения. Обозначим через Δх неопределенность координаты, а через Δр — неопределенность, с которой задается импульс. Тогда соотношение неопределенностей запишется в виде

 

 

где h — постоянная Планка.

Сходное соотношение связывает неточность энергии и неопределенность промежутка времени, в течение которого протекает процесс:

 

Мы привели соотношения неопределенностей без детального вывода. Такой вывод потребовал бы от нас слишком глубокого рейда в теорию микроявлений, который мы не станем предпринимать.

 

28. Гипотеза де Бройля.

Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом.

Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс.

 

29. Вероятностное представление описания динамики электронов.

30. Формула для плоской волны. Плотность вероятности локализации электрона.

Плоская волна — волна, у которой направление распространения одинаково во всех точках пространства.

Тут мы использовали :

— Время

— Амплитуда колебаний

— Волновое число

— Координата

Электро́нная пло́тность — плотность вероятности обнаружения электрона в данной точке конфигурационного пространства.

ЭЛЕКТРОННАЯ ПЛОТНОСТЬ -величина, равная числу электронов п(r)в единице объёма атомной системы. Для N-электронного атома, иона или молекулы Э. п. определяется выражением

⇐ Предыдущая1234