Главная | Обратная связь

Пути, контуры в ориентированном графе

Понятия пути и контура в ориентированном графе аналогичны понятиям маршрута и цикла в неориентированном графе.

Путем в ориентированном графе называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги.

Число дуг пути называетсядлиной пути.

Путь называется контуром, если его начальная вершина совпадает с конечной вершиной.

Путь (контур), в котором все дуги различны, называетсяпростым.

Путь (контур), в котором все вершины, кроме первой и последней, различны, называетсяэлементарным.

Понятиям ребра, маршрута, цепи, цикла в неориентированном графе соответствуют понятия дуги, пути, ориентированной цепи, контура в ориентированном графе.

Неориентированный граф	Ориентированный граф
ребро маршрут цикл	дуга путь контур

Пример.

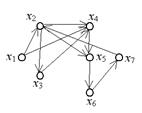
Рисунок 14.

В приведенном на рис. 14 графе выделим следующие пути:

· (x₁,x₂,x₃,x₄) – простой элементарный путь, т.к. каждая вершина и каждая дуга используются не более одного раза;

· (x₂,x₅,x₆,x₇,x₂) – простой элементарный контур, т.к. это замкнутый путь, в котором все дуги и вершины, кроме первой и последней, различны.

Гамильтонова цепь (путь, цикл, контур) − простая цепь (путь, цикл, контур), проходящая через все вершины.

Эйлерова цепь (путь, цикл, контур) − цепь (путь, цикл, контур), содержащая все ребра (дуги) графа по одному разу.

Число ребер графа можно определять различными способами. Наиболее простой способ – прямой пересчет ребер. Другой способ использует понятие степеней вершин графа.

Пример.

Рассмотрим граф типа a (см. рис. 16) и подсчитаем степени его вершин. Получим: r(А)=2, r(B)=3, r(C)=3, r(D)=2, r(E)=3, r(F)=3.. Если просуммировать степени всех вершин и разделить это число пополам, получим количество ребер графа. Так, для графа типа a имеем .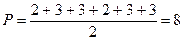

В общем случае, пусть вершины графа обозначены A_i (i = 1,n), тогда число ребер графа определяется по формуле (1)

Формула (1) для определения числа ребер графа применима как для графов с кратными ребрами, так и для графов с петлями. Следует только правильно подсчитывать степени вершин. Для этого нужно вокруг вершины провести маленькую окружность так, чтобы в нее не попала полностью петля. После чего подсчитать количество ребер, проходящих в этой окружности к вершине. Так, для вершины B графа с (см. рис. 16) получаем r(B)=5, а для вершины D того же графа r( D)=6.

Число ребер этого графа 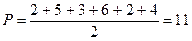, что соответствует значению, полученному прямым пересчетом.

Приведенные рассуждения позволяют сформулировать теорему о степенях вершин в графе (теорема Эйлера о рукопожатиях): в любом конечном графе количество вершин нечетной степени четно или равно нулю.

Во всех примерах графов это действительно так. Если бы был найден граф, у которого количество вершин нечетной степени было бы нечетным, то из формулы (1) следовало бы, что число ребер этого графа было бы нецелым.

Возможная интерпретация этой теоремы: на любом мероприятии (банкете, приеме и т.д.) число лиц, совершивших нечетное число рукопожатий, четно или таких лиц нет вовсе.

 

Планарность и изоморфизм графов

Геометрическим графом называется граф, у которого множество вершин – множество отмеченных точек (на плоскости или в пространстве), множество дуг – множество параметризированных отрезков непрерывных кривых (на плоскости или в пространстве), концами которых является соответствующие им вершины графа.

Все графы, приведенные в этой главе на рисунках, являются геометрическими.

Теорема. Для любого графа существует изоморфный ему геометрический граф(на плоскости или в пространстве), называемый его геометрической реализацией.

Геометрический граф называется правильно реализованным (правильным), если его дуги не имеют общих точек, отличных от вершин графа. Граф называется планарным, если он допускает правильную реализацию на плоскости.

Похожесть и непохожесть однотипных объектов в математике обозначают понятием «изоморфизм»

Графы G₁= (X₁, A₁)и G₂= (X₂, A₂) изоморфны, если существует взаимно однозначное соответствие между множествами вершин X₁и X₂, такое, что любые две вершины одного графа соединены тогда и только тогда, когда соответствующие вершины соединены в другом графе. Обозначают G₁ G₂

Изоморфные графы отличаются только нумерацией вершин.

Пример

Графы, изображенные на рис. 15 являются изоморфными.

 

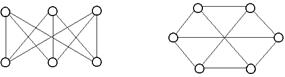
Рисунок 15

Теорема. Изоморфизм – отношение эквивалентности на множестве графов, т.е. оно рефлексивно, симметрично, транзитивно.

На основании приведенной теоремы очевидно, что изоморфизм определяет на множестве всех графов классы эквивалентности, так что каждому классу принадлежат взаимно изоморфные графы.

Изоморфизм является частным случаем другого более общего отношения – гомеоморфизма.

Пусть некоторый граф обладает ребром (a, b). Назовем операцией подразделения этого ребра операцию, соответствующую замене данного ребра парой ребер (a, x) и (x, b), где x – новая, не принадлежавшая данному графу, вершина.

Говорят, что граф G₁ является подразделением графа G₂, если G₁ может быть получен из G₂ выполнением 0 или более операций подразделения ребер.

Два графа G₁ и G₂ называются гомеоморфными, если существует общее для них подразделение G₃.

Пример.

G1

G2

G3

Рис. 16.

На рис. 16 графы G₁ и G₂ не изоморфны друг другу. Они являются гомеоморфными, так как G₃ является подразделением, общим для них.

Критерий планарности (теорема Понтрягина-Куратовского). Граф G планарен тогда и только тогда, когда ни один из его подграфов не гомеоморфен ни К_3,3, ни К₅ (рис. 17).

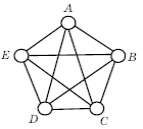Граф К5.

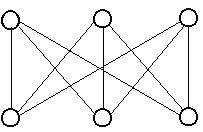Граф К3,3

Рис. 17. Графы К₅ и К_3,3 Куратовского.

Назовем замкнутую область плоского графа, ограниченную ребрами и не имеющую внутри себя никаких фрагментов графа, гранью. Грани плоского графа будет соответствовать грань многогранника, построенного путем проецирования плоского графа на сферу. Эйлер доказал, что в любом плоском графе (так же, как и в любом многограннике) число вершин В минус число ребер Р, плюс число граней равняется Г 2, т. е. В-Р+Г=2 (2).

Рассмотрим некоторый плоский граф (рис. 18).

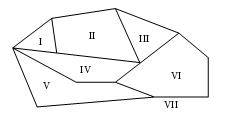
Рис. 18. Плоский граф с отмеченными гранями

Подсчитаем число ребер, вершин и граней плоского графа: P=17, B=12, Г= 7. Тогда по формуле (2) имеем 12 – 17 + 7 = 2.

Формула (2) справедлива и для графов с кратными ребрами, с петлями и с вложенными петлями (рис. 19).

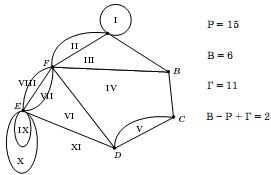
Рис. 19 Произвольный плоский граф.

В этом графе имеются грани степени 1, т. е. ограниченные только одним ребром.