Главная | Обратная связь

Задания для самостоятельной работы

1. Какое должно быть непроизводственное потребление 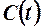на интервале времени 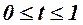для того, чтобы рост валового продукта определялся зависимостью ?

 

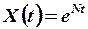2. Во сколько раз увеличится непроизводственное потребление в конечный момент времени по сравнению с начальным моментом времени 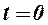, если рост валового продукта определяется зависимостью ?

 

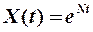3. Какие нужны капитальные вложения на интервале времени 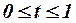для того, чтобы воспроизводство основных производственных фондов (ОПФ) определялось зависимостью ?

 

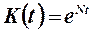4. Рассчитайте значение целевого функционала, определяющего качество изменения основных производственных фондов (ОПФ).

 

5. Во сколько раз нужно увеличить капитальные вложения в конечный момент времени 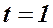по сравнению с начальным моментом времени 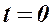для того, чтобы воспроизводство основных производственных фондов (ОПФ) определялось зависимостью ?

 

6. Рассчитать значение целевого функционала в задаче оптимального управления развитием экономики на интервале управления 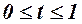при .

 

7. Рассчитать значение целевого функционала в задаче оптимального управления распределением капитальных вложений на интервале управления 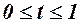при .

 

8. Для роста валового продукта, определяемого зависимостью 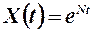, рассчитано, что непроизводственное потребление, т.е. управление в задаче оптимального управления развитием экономики, должно быть 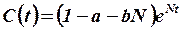. Требуется определить, во сколько раз нужно увеличить непроизводственное потребление, т.е. изменить управление в задаче оптимального управления развитием экономики, для того, чтобы рост валового продукта увеличился в раз.

 

9. Во сколько раз нужно уменьшить валовые капитальные вложения (инвестиции) 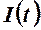для того, чтобы основные производственные фонды уменьшились с 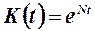до 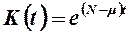в задаче оптимального управления распределением капитальных вложений?

Заключение

В представленном учебном пособии рассмотрены теоретические основы теории оптимального управления, разобран ряд примеров экономических задач данного типа. Рассмотренные в пособии задачи иллюстрируют логику теории оптимального управления, не представляют вычислительных сложностей и допускают ручной счет. В то же время большинство реальных производственных задач являются объемными, что не могут быть решены в разумные сроки без применения вычислительных средств типа ЭВМ. Обозначенный «разрыв» между уровнями требуемых средств не должен создавать впечатление недостаточной «приспособленности» изученного метода для решения реальных задач; напротив, именно на объемных трудоемких задачах достоинства и преимущества передовых математических методов проявляются наиболее отчетливо.

В этой связи представляется целесообразным обучение студентов программным средствам, позволяющим решать подобные объемные задачи и в тоже время не требующие глубокого знания программирования и нюансов математических методов. Среди таких программных средств можно отметить табличный процессор Excel пакета Microsoft Office с настройкой «Поиск решения» или OpenOffice.org Calc. Такой подход в полной мере отвечает современным тенденциям математизации наук через посредство компьютерных технологий и позволяет эффективно сочетать устоявшиеся традиционные методы преподавания математики «с мелом у доски» с использованием современных программно-технических средств.

Высокая потенциальная эффективность математизации не реализуется самопроизвольно, а требует подготовки математически грамотных специалистов. Подчас даже неглубокой математической подготовки достаточно, чтобы понять, на каком направлении деятельности предприятия или организации могут быть полезны математические оценки, прогнозы и оптимизации. Напротив, недостаточный уровень подготовки и понимания возможностей математики может служить причиной отказа от применения математических методов даже в тех случаях, когда они заведомо позволят выявить скрытые резервы и дать значительный дополнительный экономический эффект.

Не подлежит сомнению, что изучение математики формирует системность и аналитичность мышления, исключительно важные для специалистов любых направлений. При этом важно показать, что математика не есть «абстрактное искусство», демонстрирующее излишнее усложнение действительности, - ее изучение позволяет овладеть мощными методами количественного анализа, имеющими широкие практические приложения. Данное положение во многом определяет отношение студентов-экономистов ко всему циклу математических дисциплин, одним из изящных разделов которого и является теория оптимально управления в экономике.

 

 

Приложения

Приложение 1.

РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В OpenOffice.org Calc

 

В данном пункте мы изучим возможности пакета OpenOffice.org Calc при решении задач линейного программирования.

ПРИМЕР. Решить задачу линейного программирования:

Для решения подобных задач в OpenOffice.org Calc предназначена команда Поиск решения из меню Сервис.

В случае если этот пункт подменю отсутствует, необходимо просто установить расширение scsolver.uno.oxt (http://kohei.us/ooo/solver). Последняя версия Solver (от 28 ноября 2007 года) позволяет решать задачи как линейного, так и нелинейного программирования. Эта версия стала более стабильной, кроме того появилась поддержка русского языка. Для этого выполните команду в окне OpenOffice.org Calc Сервис→ Управление расширениями..., затем щелкните на кнопку Добавить (рис. П.1.1), и отыщите в вашей файловой системе файл scsolver.uno.oxt (рис. П.1.2). Нажатие на кнопку Открыть приведет к автоматической установке расширения. Однако для того, чтоб начать его использовать, нужно закрыть и снова запустить OpenOffice.org Calc.

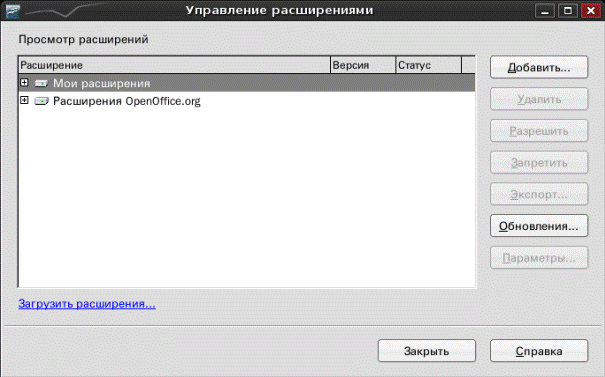
Рис. П.1.1.

 

Пусть значения 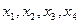хранятся в ячейках A1:A4. А значение функции L в ячейке С1. Введем ограничения:

С2 =-5*A1-A2+2*A3

С3=-А1+А3+А4

С4=-3*А1+5*А4.

 

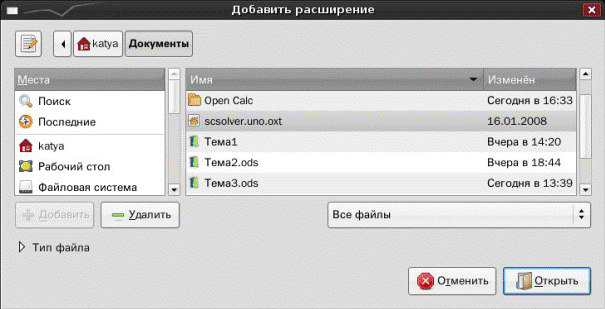
Рис. П.1.2.

Таким образом, мы задали условие исходной задачи линейного программирования.

Выполним команду из главного меню Сервис→Поиск решения, появится окно Оптимальное решение, представленное на рис. П.1.3.

 

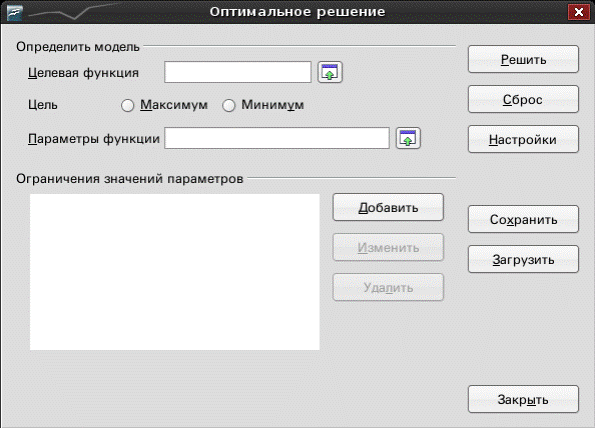
Рис. П.1.3.

 

Устремим целевую функцию в ячейке C1 к минимуму. Для этого введем в поле Целевая функция введем ячейку С1 и установим опцию Минимум. В поле Параметры функции необходимо указать адреса ячеек, в которых хранятся изменяемые значения. В нашем случае это ячейки А1:А4.

Для добавления ограничений необходимо щелкнуть по кнопке Добавить, появится диалоговое окно Ограничение (рис. П.1.4). В поле ввода Ячейка необходимо ввести адрес ячейки, где хранится ограничение, затем, щелкнув по стрелке, выбрать знак и ввести конкретное значение ограничения в поле Ограничение. Щелчок по кнопке OK означает ввод очередного ограничения и возврат к диалоговому окну Оптимальное решение.

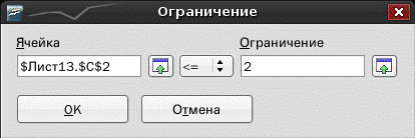
Рис. П.1.4.

 

В нашем случае окно будет иметь вид, изображенный на рис. П.1.5. Щелчок по кнопке Решить начнет процесс решения задачи, который завершится появлением системного диалогового окна, сообщающего, что решение найдено.

 

Рис. П.1.5.

 

Щелчок по кнопке OK приведет к появлению в ячейке С1 значения целевой функции L, а в ячейках A1:A4 - значений переменных 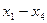, при которых целевая функция достигает минимального значения.

Итак, назначение основных кнопок и окон диалогового окна Оптимальное решение:

Поле Целевая функция - определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению.

Опции Максимум и Минимум определяют, что необходимо сделать со значением целевой ячейки - максимизировать, минимизировать или сделать равным конкретному значению.

Поле Параметры функции определяет изменяемые ячейки. Изменяемая ячейка - это ячейка, которая может быть изменена в процессе поиска решения для достижения нужного результата.

Окно Ограничения значений параметров перечисляет текущие ограничения в данной задаче. Ограничение есть условие, которое должно удовлетворяться решением; ограничения перечисляются в виде ячеек или интервалов ячеек, обычно содержащих формулу, которая зависит от одной или нескольких изменяемых ячеек, чье значение должно попадать внутрь определенных границ или удовлетворять равенству.

Кнопки Добавить, Изменить, Удалить позволяют добавить, изменить или удалить ограничение.

Кнопка Решить запускает процесс решения определенной задачи.

Кнопка Закрыть закрывает окно диалога Оптимальное решение, не решая проблемы.

Кнопка Сброс очищает все текущие установки задачи и возвращает все параметры к их значениям по умолчанию.

Кнопка Настройки выводит окно диалога, в котором можно контролировать различные аспекты процесса отыскания решения (рис. П.1.6).

Рис. П.1.6.

 

С помощью решающего блока можно решить множество различный оптимизационных задач (задач на максимум и минимум) с ограничениями любого типа. При решении задачи целочисленного программирования необходимо добавить ограничение, показывающее, что переменные целочисленные. При решении других оптимизационных задач вводят целевую функцию и ограничения.

 

Приложение 2.

Планирование центром оптимального распределения капитальных вложений между предприятиями методом динамического программирования

 

Метод ДП может быть использован как для динамических, так и для статических систем. Здесь приведен пример использования метода ДП для оптимального распределения ресурсов, то есть для решения статической оптимизационной задачи. Смысл этой задачи состоит в следующем: центр должен так распределить имеющиеся у него капитальные вложения между своими предприятиями, чтобы суммарная отдача от этих вложений для центра была максимальной.

Целевая функция центра при этом имеет следующий вид:

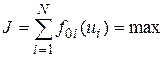(П.2.1)

 

где функция f_0i характеризует эффективность (отдачу) капитальных вложений u_i в i-ое предприятие для центра, N - число предприятий.

Типичная зависимость функций f_0i(u_i) приведена на рис П.2.1.

Рис. П.2.1. Типичная зависимость эффективности

капитальных вложений

 

Зависимости f_0i(u_i), приведенные на рис. П.2.1, можно аппроксимировать экспонентой или параболой. Возьмем последнюю как более простую функцию вида:

,

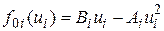где A_i, B_i - известные центру коэффициенты аппроксимирующих функций, A_i > 0, B_i > 0. Известен также суммарный объем капитальных вложений 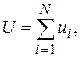подлежащий распределению между предприятиями, u_i - доля капитальных вложений в i - ое предприятие.

Для постановки задачи в классическом виде введем новую целевую функцию:

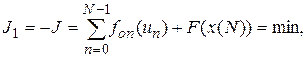(П.2.2)

где n = i - 1 – новая нумерация предприятий от нуля до N - 1,

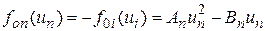
n = 0 ¸ N - 1.

Для описания процесса распределения ресурсов между предприятиями введем разностное уравнение вида:

x(n + 1) = x(n) + u(n), n = 0 ¸ N - 1, (П.2.3)

где x - сумма распределенного капитала,

u - доля капитала, выделенная n-ому предприятию.

Задано ограничение на долю капитала в виде u(n) ³ 0, начальное условие x(0) = 0.

При этом ограничение 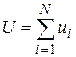примет следующий вид x(N) = U. Это означает, что в процессе распределения

 

надо так раздавать капиталы (ресурсы), чтобы после их раздачи у центра ничего не осталось. В противном случае, если все значения u(n) = 0, то весь капитал останется у центра, что противоречит условиям задачи. Эта ситуация должна быть наказана. Для этого терминальную функцию F(x(N)) зададим в виде:

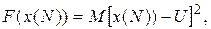(П.2.4)

где M - коэффициент штрафа центру, зададим его очень большим числом.

Тогда с учетом (П.2.2) и (П.2.4) получим:

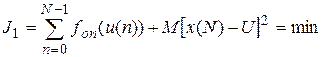. (П.2.5)

Эта целевая функция совместно с разностным уравнением (П.2.3) и заданными ограничениями ставит оптимизационную задачу планирования центру.

Решение. Для сформулированной задачи запишем уравнение Беллмана с краевым условием:

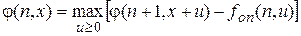
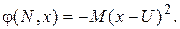
тогда ,

где u_оп(n, x) - оптимальное распределение ресурсов центра для n-ого предприятия.

Пусть число предприятий N = 3, суммарный ресурс капитальных вложений центра U = 10(млн. руб.), а функции f_0i заданы в виде:

f₀₁ = 16u - 0,4u²

f₀₂ = 18u - 0,6u² (П.2.6)

f₀₃ = 25u - 0,7u²

При новой нумерации предприятий от нуля до N - 1 = 2 с учетом (П.2.2) имеем:

f₀₀ = - f₀₁ = 0,4u² – 16u

f₀₁ = - f₀₂ = 0,6u² – 18u

f₀₂ = - f₀₃ = 0,7u² – 25u

Оптимальное решение задачи планирования будем искать методом ДП от второго предприятия к нулевому.

При n = 2 уравнение Беллмана:

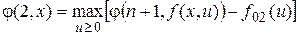
а с учетом краевого условия j(3,x) = - M(x - u)² оно примет вид:

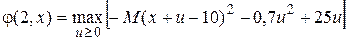
так как U = 10 , a f₀₂(u) = 0,7u² – 25u.

Поскольку число М >> 0, то для максимизации j оптимальное значение u_оп(2) должно обратить в нуль значение в круглых скобках, то есть (x + u_оп-10) =0, откуда u_оп(2) = 10 – x. При этом

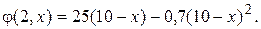
При n = 1 получим следующее уравнение Беллмана:

 

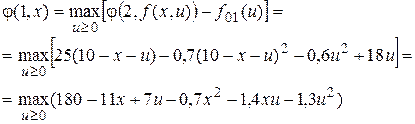
Возьмем от выражения в скобках производную по u и приравняем ее к нулю. В результате получим: 7 - 1,4x - 2,6u_оп = 0

или b - 2,6u_on = 0, где b = 7 - 1,4x.

На рис. П.2.2 построены прямые вида y = b – 2,6u_оп при различных значениях коэффициента b = 7 – 1,4x.

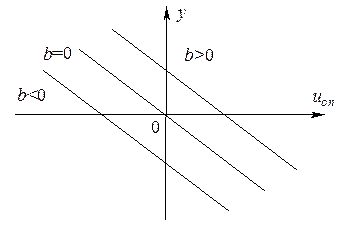
Рис. П.2.2. Прямые вида y = b – 2,6u_оп при

разных значениях коэффициента b

Так как по условиям задачи u ³ , то оптимальное значение u_оп(1) будет определяться по выражению:

 

Подставим это значение u_оп(1) в выражение для j(1, x) и получим:

 

При n = 0 уравнение Беллмана примет вид:

 

 

После раскрытия скобок и приведения подобных членов получим:

 

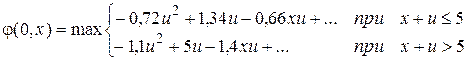
Здесь многоточие означает слагаемые, не зависящие от u.

Так как по условиям задачи u > 0, то неравенства x + u £ 5 и x + u > 5 приводят к условию 0 £ x £ 5.

Возьмем производную 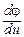при x + u £ 5 и приравняем ее нулю. В результате получим: -1,44u + 1,34 - 0,66x = 0 или -1,44x + b = 0, где b = 1,34 - 0,66x.

По аналогии при n = 1 здесь получим значение оптимального управления

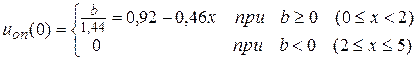
Теперь возьмем производную 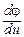при x + u > 5 и приравняем ее нулю:

- 2,2u + 5 – 1,4x = 0 или - 2,2u + b = 0

где b = 5 – 1,4x, откуда

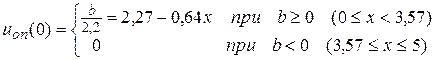
Так как мы получили два разных результата для u_оп(0), следовательно, эта задача имеет два оптимальных решения.

Приведем одно из этих решений для первого выражения

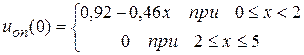
Так как x(0) = 0, то по этому выражению получим u_оп(0) = 0,92 (млн. руб.)

Тогда x(1) = x(0) + u_оп(0) = 0 + 0,92 = 0,92.

Для этого значения x определим u_оп(1) по соотношению, полученному при n = 1.

u_оп (1) = 2,69 – 0,54 ´ 0,92 = 2,19 (млн. руб.)

Тогда x(2) = x(1) + u_оп(1) = 0,92 + 2,19 = 3,11.

Для этого значения x определим u_оп(2) по соотношению, полученному при n = 2

u_оп(2) = 10 – 3,11 = 6,89 (млн. руб.).

Убедимся, что u_оп(0) + u_оп(1) + u_оп(2) = 0,92 + 2,19 + 6,89 = 10 (млн. руб.) = U.

В таблице П.2.1 приведены результаты расчетов функций f_0i и целевой функции центра J по приведенным выше формулам (П.2.6) и (П.2.2) при оптимальном планировании.

Таблица П.2.1

i
uоп(i)	0,92	2,19	6,89
f0i	14,38	36,54	138,86	J = 189,78

В таблице П.2.2 приведены результаты расчетов функций f_0i и целевой функции центра 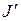по формулам (13) и (8) при неоптимальном планировании, когда все получили поровну, то есть при (млн. руб.).

Таблица П.2.2

i
u(i)	3,333	3,333	3,333
f0i	48,84	53,28	75,48	J = 177,6

Из этой таблицы видно, что при неоптимальном планировании получили 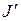= 177,6 < 189,78.

Второе оптимальное решение поставленной задачи найдем при использовании второго выражения

Так как x(0) = 0, то из этого выражения получим u_оп(0) = 2,27 (млн. руб.).

Тогда x(1) = x(0) + u_оп(0) = 2,27. Для этого значения x(1) получим u_оп(1) = = 2,69 – 0,54 ´ 2,27 = 1,464 (млн. руб.). Тогда x(2) = x(1) + u_оп(1) = 3,734.

Для этого значения x(2) получим:

u_оп(2) = 10 - 3,734 = 6,266 (млн. руб.).

Проверка: u_оп(0) + u_оп(1) + u_оп(2) = 10 (млн. руб.) = U.

Для этого варианта планирования значения функций f_0i и целевой функции центра J по формулам (П.2.6) и (П.2.1) приведены в таблице П.2.3. Из нее следует, что этот максимум меньше первого.

Таблица П.2.3

i
uоп(i)	2,27	1,464	6,266
f0i	34,26	25,066	129,166	J = 188,5

Если отдать весь капитал третьему предприятию, то есть u(1) = 0, u(2) = 0, а u(3) = 10 (млн. руб.), то целевая функция центра составит:

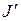= f₀₃ = 25u(3) – 0,7u²(3) = 250 – 0,7 ´ 100 = 180 < 189,78.

Таким образом приведенные расчеты показывают, что только при оптимальном распределении капиталовложений между предприятиями целевая функция центра достигает своего максимального значения.

 

Приложение 3.